|
|
Плоские прямоугольные координатыАстрономические и геодезические координатные системы трудно применять на практике для обоснования съемочных и инженерных работ. Погрешность определения координат, даже при точных измерениях, остается довольно большой. При определении широты она составляет в дуговой мере 0,1 – 0,2"; при определении долготы 0,3 – 0,5", что в линейной мере равно соответственно 3 – 6 и 5 – 10 м. Поэтому в практику геодезических и топографических работ была введена система плоских прямоугольных координат (рис. 3). По сути дела, это известные декартовы координаты, хотя в геодезии принята правая система координат – оси X и Y поменялись местами.
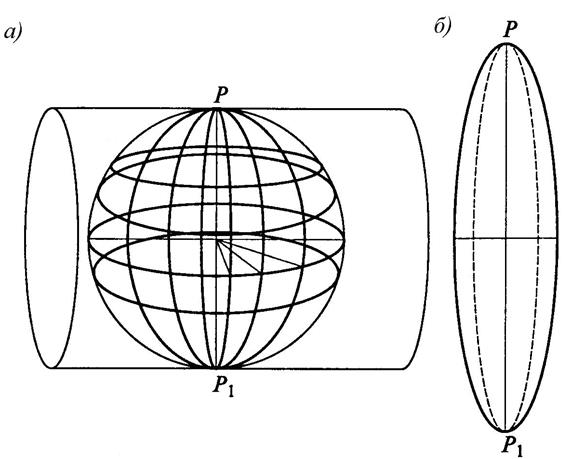
Рис. 3. Оси прямоугольной системы Особенность прямоугольных координат заключается в том, что они могут быть наложены на плоское изображение земной поверхности. Для этого она должна быть изображена в некоторой картографической проекции. Общие понятия о картографических проекциях При создании карт поверхность эллипсоида вращения, как математическая поверхность Земли, не может быть развернута на плоскости без складок или разрывов, поэтому используют картографические проекции, в которых отображение поверхности эллипсоида на плоскости происходит по определенным математическим законам. Эти законы выражают функциональную связь координат точек картографируемой поверхности и плоскости. В основу такого отображения картографической проекции положена система геодезических координат, координатными линиями которой являются меридианы и параллели. Линии меридианов на картографируемой поверхности получают путем сечения ее плоскостями, проходящими через ось вращения эллипсоида (они будут эллипсами), а линии параллелей – путем сечения картографируемой поверхности плоскостями, перпендикулярными к оси вращения эллипсоида (параллели имеют вид окружностей). Эти же координатные сетки в виде меридианов и параллелей на картах строят по определенным математическим правилам. Возможен выбор различных правил перехода к плоскости, т. е. построение изображения в разных картографических проекциях. Математическая основа картографических проекций позволяет производить на картах точные измерения. Однако для этого нужно знать закон распределения искажений каждой проекции. Картографические проекции различают по разнообразным признакам, прежде всего по характеру сохраняемых свойств и виду сетки меридианов и параллелей. По первому признаку проекции делят: на равновеликие, сохраняющие площади; равноугольные (или конформные) проекции, которые сохраняют углы и, следовательно, формы контуров, но сильно искажают соотношение размеров (например, проекция Меркатора); проекции, сохраняющие длины линий в некоторых направлениях или во всех направлениях из одной какой-нибудь точки; производные, не сохраняющие полностью никаких свойств, но более или менее удобные для потребителя карты, распределяющие искажения по всему изображению. В геодезии и топографии применяют проекцию Гаусса–Крюгера – это такое конформное (подобное) равноугольное изображение поверхности земного эллипсоида на плоскости, при котором осевой меридиан изображают прямой линией с сохранением масштаба, экватор – также прямой, перпендикулярной осевому меридиану, а все остальные меридианы и параллели – кривые линии. Проекция Гаусса–Крюгера В любой проекции изображение получается тем более искаженным, чем больше картографируемая территория. Поэтому прямоугольная система координат не может быть распространена на большую территорию. Приходится решать задачу по частям. В 1825 г. К.Ф. Гаусс впервые решил общую задачу по изображению одной поверхности на другой с сохранением подобия в бесконечно малых частях. Частным случаем этой задачи является отображение поверхности эллипсоида вращения на плоскости. Предложенная К.Ф. Гауссом проекция практически не применялась. В 1912 г. А. Крюгер вывел и опубликовал рабочие формулы этой проекции. После этого проекция получила название проекции Гаусса–Крюгера и нашла широкое применение в топографо-геодезических работах. Геометрическая интерпретация проекции Гаусса–Крюгера выглядит следующим образом. Поверхность земного эллипсоида условно делят меридианами на зоны, соответствующие 6° по долготе. Средний меридиан зоны называется осевым. Затем эллипсоид вписывается в поперечно расположенный цилиндр так, чтобы плоскость его экватора совместилась с осью цилиндра, а один из осевых меридианов оказался касательной к его боковой поверхности. Эту зону, а затем и последующие по определенному математическому закону проецируют на внутреннюю боковую поверхность цилиндра (рис. 4, а). После проецирования поверхность цилиндра разворачивают в плоскость, разрезав цилиндр по образующим, касательным земных полюсов. Спроецированные аналогично последовательно одна за другой зоны соприкасаются между собой в точках, расположенных по линии экватора, как это показано на рис. 5, а.
Рис. 4. Схема образования проекции Гаусса–Крюгера: а – геометрическое представление получения изображения зоны;
Получается, что вся поверхность Земли разбивается на 60 зон, считая от начального – Гринвичского меридиана (0°). Через каждую зону от Северного до Южного полюса проходит прямолинейный осевой меридиан зон. Долгота осевого меридиана n-й зоны равна (6n – 3)°. Нумерация зон идет с запада на восток, начиная от Гринвичского меридиана. Территория России располагается примерно в 28 зонах: от 4 до 32. В пределах каждой зоны плоская координатная система располагается самостоятельно. Оси X и Y размещаются по осевому меридиану зоны и экватору. Начало отсчета координат в их пересечении. Поскольку территория России расположена в северном полушарии, то все значения х всегда будут положительными. Значения координаты у могут быть в каждой зоне и положительными и отрицательными. Чтобы избежать этих неудобств, начало отсчета ординат искусственно сдвигают на запад на 500 км (рис. 5). Другими словами, к значению у прибавляют 500 км. Ширина полузоны по долготе составляет всего 3°, т. е. порядка 333 км, поэтому все значения у станут положительными. Поскольку в каждой зоне координаты могут совпадать, в значении у указывается также номер зоны. Например, если координаты точки даны в виде: х = 6 650 457, у = 4 307 128, то это значит, что точка расположена от экватора на расстоянии 6 650 457 м; в значении координаты у цифра 4 означает номер зоны, а от оставшегося числа следует отнять 500 000 м, тогда получим расстояние нашей точки от осевого меридиана, а именно – 192 872 м. Такие координаты называют преобразованными. Для удобства пользования плоскими координатами каждую зону покрывают сеткой квадратов, так называемой километровой сеткой (сторона квадрата равна 1 км), которая изображается на топографических картах масштаба 1:10 000; 1:25 000; 1:50 000 (на картах масштаба 1:100 000 квадраты двухкилометровые; 1:200 000 – от 4 до 10 км).
Рис. 5. Зональная система координат в проекции Гаусса–Крюгера: а – деление поверхности Земли на зоны (1 – осевой меридиан, 2 – экватор);
Такая зональная система координат, принятая в качестве государственной, обеспечивает возможность построения на территории всей Земли системы плоских прямоугольных координат и позволяет получать практически без искажений довольно большие участки земной поверхности. 2.6. Искажения при изображении поверхности эллипсоида Представим участок земной поверхности в виде части поверхности сферы радиусом R, который заменяется частью горизонтальной плоскости. Из рис. 6 видно, что с удалением от точки m разница DS в длине дуги S и ее проекции на плоскость S' возрастает, а расстояние между ними (высота точки местности)
Сделав ряд преобразований, запишем
Можно также определить значение Dh, учитывая малость Dh относительно R и близость S и S',
Рис. 6. Искажение длины линии и изменение высоты точки Из расчетов по полученным формулам следует, что при длине линии 10 км DS составляет только 1:1 000 000 ее длины. Поэтому считается, что участок радиусом 10 км можно принять за плоский при съемке планов без рельефа. Значительно быстрее возрастают расхождения между высотами точек на сфере и на плоскости. При той же длине линии 10 км разность высот достигает уже 7,8 м, поэтому значение Dh можно не учитывать лишь при расстояниях меньше 1 км. 2.7. Полярные координаты. Связь плоской прямоугольной Система полярных координат может быть задана на плоскости, сфере или поверхности эллипсоида и состоит из точки М – начала координат (рис. 7) и полярной оси МA, относительно которых положение точки определяется координатами: углом положения a (дирекционный угол или румб на плоскости, азимут на сфере и эллипсоиде) и кратчайшим расстоянием S между точками М и М1, считаемым по поверхности. За полярную ось (начальное направление) обычно принимают: на плоскости – направление, параллельное оси абсцисс прямоугольных координат, а на сфере и эллипсоиде – северное направление меридиана, проходящего через точку М. Связь плоской прямоугольной и полярной систем координат осуществляется путем решения прямой и обратной геодезических задач.
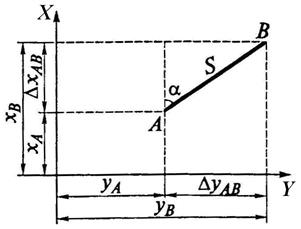
Прямая геодезическая задача. Задача формулируется так: заданы хА и уА – плоские геодезические координаты точки А (рис. 8). Измерено непосредственно в натуре расстояние S между точками и a – угол положения (направления). Находим приращения координат (см. рис. 8):
Получаем искомые координаты точки В:
Обратная геодезическая задача. Заданы хА и уА; хB и уB – координаты точек А и В (см. рис. 8). Следует найти угол положения и расстояние SAB. Из рисунка видно, что
Системы отсчета времени По рекомендации Международного астрономического союза с 1991 г. введены три шкалы времени: барицентрическое координатное время За основную единицу измерения времени принимается продолжительность одного полного оборота Земли вокруг своей оси, называемая сутками. В зависимости от принятого начала отсчета и используемых единиц в астрономии различают две системы измерения времени: звездную и солнечную. Из-за неравномерности вращения Земли и постоянно возрастающих требований науки и техники было введено равномерно текущее, так называемое, эфемеридное, время, связанное не с суточным вращением Земли, а с годичным движением Земли вокруг Солнца – тропическим годом. Единицы эфемеридного времени постоянны с точностью до 1 × 10-10. Для составления эфемерид Солнца, Луны и планет используют эфемеридное время. С 1 января 1972 г. во всех службах времени введено атомное время (AT), не зависящее от вращения и движения Земли. За единицу атомного времени принята секунда, которая равна 9192 631770 периодам колебаний излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. Точность атомных часов порядка 1 × 10-12. Стабильность частоты современных квантовых генераторов на атомном водороде достигает 5 × 10-14. Все передаваемые отечественными радиостанциями сигналы времени формируются на основе единообразной системы атомного времени и шкалы, воспроизводимой Государственным эталоном времени и частоты, которая согласована со шкалой UTC МБВ (Международного бюро времени). 3. Определение местоположения 3.1. Общие сведения об определении положения точек Еще с доисторических времен для ориентирования человек использовал небесные светила. Обычно мореплаватели ориентировались по звездам, указывающим направление движения: зная среднюю скорость и время в пути, можно было сориентироваться в пространстве и определить расстояние до конечного пункта назначения. Однако при плохих погодных условиях сбиться с курса не представляло особого труда. С появлением компаса задача значительно упростилась, так как уменьшилась зависимость от погоды. Позднее для определения местоположения в океане, т. е. в навигации, использовались угловые наблюдения небесных тел. Но даже при самых точных угловых наблюдениях небесных тел ошибка определения местоположения этим методом составляла не менее 1 мили. Вместе с тем требуемая точность существенным образом зависит от вида работ, типа транспортного средства и условий передвижения. Например, для безопасного управления судами в открытом океане необходимая точность местоопределения составляет несколько километров, в то время как в прибрежных водах – 2 – 5 м. Аналогичны требования к точности и для воздушных судов. Во время полета над океаном требуемая точность определения высоты самолета составляет около 100 м, а при посадке на этапе глиссады для пассажирского самолета – 0,3 м. Появление искусственных спутников Земли произвело переворот в методах геодезии и значительно повысило точность навигации и определения положения точек и объектов на поверхности Земли. С созданием радиолокационных станций стало возможным измерять параметры движения и относительное местоположение спутника по отраженному от его поверхности лучу радиолокатора. Появилась возможность измерения параметров движения спутника по излучаемому сигналу. В 1957 г. в СССР группа ученых под руководством В.А. Котельникова экспериментально подтвердила возможность определения параметров движения искусственного спутника Земли (ИСЗ) по результатам измерений доплеровского сдвига частоты сигнала, излучаемого этим спутником. При этом была установлена возможность решения обратной задачи – нахождения координат приемника по измеренному доплеровскому сдвигу сигнала, излучаемого с ИСЗ, если параметры движения и координаты этого спутника известны. При движении спутник излучает сигнал определенной частоты, который несет информацию об его положении на орбите. Если измерить частоту принятого сигнала и сравнить ее с эталонной, то можно вычислить доплеровский сдвиг частоты, обусловленный движением спутника. При непрерывном измерении можно составить своего рода функцию изменения частоты Доплера (т. е. доплеровского сдвига частоты). Частота Доплера непрерывно изменяется и в определенный момент становится равной нулю, затем изменяет знак. В момент равенства нулю частоты Доплера приемник находится на линии, которая является нормалью к вектору движения спутника. Измерив момент времени, когда частота Доплера равна нулю, и используя зависимость крутизны кривой доплеровской частоты от расстояния между приемником и ИСЗ, можно вычислить координаты приемника. При этом спутник становится радионавигационной опорной станцией, координаты которой изменяются во времени вследствие движения спутника по орбите, но заранее могут быть вычислены для любого момента времени благодаря эфемеридной информации, заложенной в навигационном сигнале спутника. В 1963 г. начались работы по построению первой отечественной низкоорбитальной навигационной спутниковой системы «Цикада», в 1967 г. на орбиту был выведен первый отечественный навигационный спутник «Космос-192». Для радионавигационных спутниковых систем первого поколения характерным является применение низкоорбитальных ИСЗ и использование для измерения навигационных параметров объекта сигнала одного, видимого в данный момент спутника. Ошибка в определении координат для подвижного объект составляла ~500 м. Для неподвижного объекта эта величина уменьшается до 50 м. Идеи использования космических аппаратов для навигации подвижных объектов в США начали развиваться после запуска в СССР 1957 году первого искусственного спутника Земли. В это время была поставлена задача слежения за советским ИСЗ посредством приема его сигнала на наземном пункте с известными координатами, выделения доплеровского сдвига несущей частоты передатчика ИСЗ и дальнейшего расчета параметров движения спутника. Одновременно решалась и обратная задача расчета координат приемника на основе обработки принятого сигнала и координат ИСЗ. На этой основе в интересах навигационного обеспечения в 1964 г. была создана доплеровская спутниковая радионавигационная система первого поколения «Transit», предназначенная для навигационного обеспечения пуска с подводных лодок баллистических ракет «Поларис». После того, как в 1967 г. эта система была предоставлена для коммерческого использования, число гражданских потребителей быстро превысило число военных. Координаты потребителя рассчитывались на основе приема и выделения доплеровского сдвига частоты передатчика одного из 6 – 7 навигационных космических аппаратов, который мог находиться в поле видимости в течение примерно 40 мин. Так же, как и в системе «Цикада», в системе «Transit» координаты источника вычисляются по доплеровскому сдвигу частоты сигнала одного из 7 видимых спутников, которые имеют круговые полярные орбиты с высотой над поверхностью Земли ~ 100 км. Период обращения спутников «Transit» равен 107 минутам. Спутниковые низкоорбитальные доплеровские радионавигационные системы имеют ряд существенных недостатков: это невысокая точность определения координат объектов и отсутствие непрерывности в измерениях, так как спутники имеют низкие орбиты, и поэтому время, в течение которого спутник находится в поле видимости потребителя, не превышает одного часа. Кроме того, время между прохождением различных спутников зоны видимости зависит от географической широты, на которой он находится, и может составить величину от 35 до 90 минут. Сокращение этого времени за счет наращивания числа спутников невозможно, потому что все спутники излучают сигналы на одной и той же частоте. Для определения взаимного расположения спутников их можно синхронно наблюдать с нескольких наземных станций. Сам спутник при этом может играть пассивную роль (например, отражая луч лазера, посланный с наземной станции, обратно на ту же станцию) или активную роль (непрерывно осуществляя передачу радиосигнала). На первых этапах развития космической геодезии сигналы подавались в виде вспышек света, которые фотографировались на фоне звезд одновременно с нескольких наземных пунктов, находящихся вне прямой видимости. Положение спутника на фотографии относительно опорных звезд давало возможность определить точное направление на него с данной станции наблюдения. В настоящее время для определения местоположения на земной поверхности обычно измеряют расстояние между наземным пунктом и спутником, а также скорость изменения этого расстояния при прохождении спутника. Расстояния рассчитывают, исходя из времени, которое затрачивает электромагнитный сигнал (лазерная вспышка или радиоимпульс) на прохождение пути от спутника до принимающей станции при условии, что скорость распространения сигнала известна. Скорость изменения расстояния между спутником и принимающей станцией определяется по величине наблюдаемого доплеровского сдвига частоты – изменения частоты сигнала, поступающего со спутника. Вводятся поправки за атмосферную задержку сигнала и рефракцию. Основной принцип спутниковой геодезии – это использование трилатерации, т. е. измеряются расстояния до спутников, являющихся точками отсчета для вычисления координат на Земле. Все остальное, что относится к системе, – всего лишь технические решения, предназначенные для облегчения этого процесса, для того чтобы выполнить его точнее и проще. Начало этим работам, как в СССР, так и в США положило появление в 1960 году атомных часов, что позволило создать для целей навигации сеть точно синхронизированных передатчиков, передающих кодированные сигналы. Координаты приемника определялись по временным задержкам сигнала. В том случае, когда измеряется расстояние до одного спутника с известными координатами, местоположение определяемой точки должно быть на воображаемой сфере с центром, находящимся на этом спутнике, и радиусом R, равным измеряемому расстоянию S1 (рис. 9, а). Когда одновременно измеряется расстояние S2 до второго спутники, то область поиска сократится, так как местоположение определяемой точки будет находиться на линии пересечения двух сфер с радиусами S1 и S2, т. е. на окружности (рис. 9, б). В случае измерения расстояния S3 до третьего спутника возможное местоположение определяется двумя точками пересечения окружности со сферой радиуса S3 (рис. 9, в).
Рис. 9. Определение местоположения точки: Одну из этих двух точек можно не принимать во внимание, так как одна из точек располагается слишком далеко от поверхности Земли либо имеет неправдоподобно большую скорость движения. Например, когда точно известна высота определяемой точки (например, корабли всегда находятся на уровне моря), то можно исключить одно из измерений. Одну из сфер на рисунках можно заменить на сферу с центром в центре Земли и радиусом, равным ее радиусу плюс высота. Некоторые приемники могут быть переключены в режим определения двух горизонтальных координат. Для того чтобы определить истинное местоположение по этим двум точкам (рис. 9, в), можно измерить расстояние S4 до четвертого спутника. Можно обойтись и тремя спутниками, если логически исключить неправдоподобное решение. Различные методы наблюдений позволяют определять абсолютное и относительное положение объектов на земной поверхности. При определении абсолютного положения используется не менее трех спутников. Чтобы компенсировать разницу в точности определения времени по часам, установленным на борту спутников и на наземной станции, обычно требуется еще и четвертый спутник. Определение относительного положения пункта на земной поверхности требует одновременного наблюдения с четырех и более спутников с двух (или более) наземных станций. Для определения координат точек на земной поверхности в геоцентрической системе необходимо знать элементы орбит спутников в этой же системе, так как любые погрешности в их определении вызывают ошибки получаемых данных. Эти погрешности могут быть уменьшены путем осреднения наблюдаемых величин за несколько дней, недель или месяцев. Часть систематических погрешностей в расчетах элементов орбиты примерно в одинаковой степени вносит искажения при определении всех точек и, поэтому, при определении их взаимного положения компенсируется. Вследствие этого относительные положения точек на земной поверхности обычно определяются с большой точностью. В зависимости от числа одновременно работающих принимающих станций и одновременно наблюдаемых спутников можно получать определенные различия между принимаемым и передаваемым сигналами; это позволяет исключить влияние неизвестных факторов. В спутниковых методах определения местоположения измерение расстояний до спутников осуществляется по измерениям времени прохождения радиосигнала от космического аппарата до приемника. При этом передающее устройство размещено на спутнике, а приемник – на определяемой точке. Радиосигнал проходит измеряемое расстояние S от спутника (передатчика) до приемника за время х. Время излучения и время приема данного сигнала точно определяют синхронизированными часами, которые расположены на спутнике и на определяемой точке. При этом измеряемое расстояние определяют по формуле:
Так как скорость v радиоволны составляет около 300 000 км/с, то для обеспечения геодезической точности измерений необходимо измерять время с точностью 10-10 – 10-12 с. Главной трудностью при измерении времени распространения радиосигнала является точное выделение момента времени, в который сигнал передан со спутника. Для обеспечения высокой точности измерений синхронизируют опорные генераторы передатчика (спутника) и приемника. В светодальномерных и радиодальномерных измерениях используются импульсные и фазовые методы измерения расстояний, а также их сочетания. Данные методы используются в спутниковых дальномерных измерениях. При этом широко используются кодированные сигналы. |
|


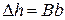 увеличивается. Из данных рис. 6 получаем
увеличивается. Из данных рис. 6 получаем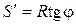 ;
; 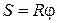 ;
; 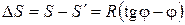 .
.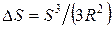 . (1)
. (1) . (2)
. (2)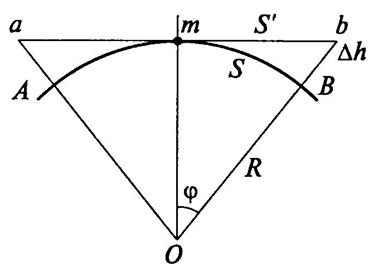
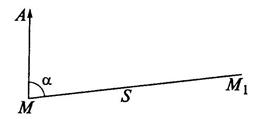
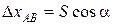 ;
;  . (3)
. (3)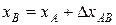 ;
; 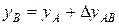 . (4)
. (4) ;
; 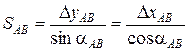 ; (5)
; (5) . (6)
. (6)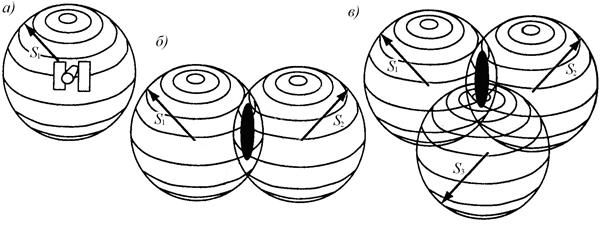
 . (7)
. (7)