|
|
Определение относительного положения пунктов по разностям фазЕсли фазовые измерения псевдодальностей до одного и того же спутника выполнены одновременно в двух пунктах, то они содержат очень близкие по величине погрешности орбиты и внешней среды. Разности таких измерений практически лишены указанных погрешностей. Поэтому, используя разности фаз, удаётся с высокой точностью определять положение одного пункта относительно другого. Рассмотрим возникающие при таком подходе фазовые уравнения. Первые разности фаз.Пусть в пунктах A и B выполнены фазовые измерения на один и тот же спутник s. Рассмотрим результаты измерений на обоих пунктах, относящиеся к одному и тому же положению спутника, то есть - к одному моменту спутникового времени. Благодаря наличию в излучаемом спутником сигнале меток времени это возможно. Составим для обоих измерений уравнения вида (13), при этом в одном уравнении вместо индекса i, обозначающего номер пункта, будем иметь A, а в другом - B. Образуя разность этих уравнений, получим уравнение разности фаз
Обозначая в полученном выражении для краткости каждую разность одним символом с двумя соответствующими нижними индексами, запишем
Пусть координаты одного из пунктов, например A, известны. Тогда неизвестными в уравнении (15) будут входящие в Вторые разности. Если в пунктах A и B выполнены измерения на два спутника (s и k), то, записывая первые разности фаз, получим два уравнения вида (15):
Вычитая из второго уравнения первое и вновь обозначая разности одним символом, но с двумя верхними индексами, и учитывая, что
Получили уравнение, в котором уменьшено число неизвестных и, в частности, исключены систематические ошибки смещений часов приёмников A и B. В каждую эпоху наблюдений двух спутников с двух пунктов формируется такое уравнение. Неизвестными в уравнении (16) являются три координаты x, y, z пункта B и число N. При числе наблюдаемых спутников ns и числе эпох nt можно составить (ns - 1)nt независимых разностей фаз. Значит, число таких уравнений будет равно (ns - 1)nt, а число неизвестных - 3 +(ns - 1). Теперь, чтобы число уравнений оказалось не меньше числа определяемых неизвестных, при наблюдении четырёх спутников число эпох должно быть не меньше чем 2, а при наблюдении двух спутников – не менее чем 4. Решая такую систему уравнений, вычисляют координаты xB, yB, zB пункта B и ns - 1 чисел N. Третьи разности. Выполнив в две эпохи t1 и t2 измерения, аналогичные тем, которые позволили составить уравнение (16), получим два таких уравнения:
Образуя их разность, освобождаемся от неоднозначностей N и получаем уравнение
где
и
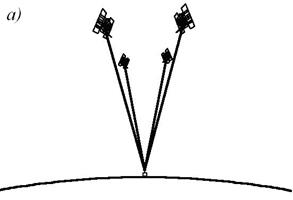
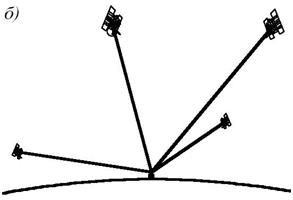
- Число неизвестных ещё уменьшено и теперь равно трем, - это координаты пункта B,а число уравнений равно (ns - 1)(nt - 1). Необходимое неравенство (ns - 1)(nt - 1) ³ 3 приводит к условию nt ³ (ns + 2)/(ns - 1), означающему, как и в предыдущем случае, необходимость выполнения при контакте с четырьмя спутниками не менее двух эпох измерений, а при контакте с двумя спутниками - не менее четырёх эпох. Основные источники ошибок При приеме сигналов от пяти или большего количества спутников определение положения аппаратуры потребителя может обеспечиваться со значительной избыточностью, что допускает обнаружение недопустимых сигналов и использование данных от спутников с лучшим расположением. Однако некоторые источники ошибок, возникающих при работе GPS, являются трудно устранимыми. Задержки распространения сигнала в ионосфере и тропосфере. Описанный выше алгоритм предполагает, что сигнал распространяется с непрерывной скоростью, которая равна скорости света. Однако в реальности скорость света является константой только в вакууме. Когда сигнал проходит через ионосферу (слой заряженных частиц на высоте 130 – 290 км) и тропосферу (от 8 до 13 км от поверхности Земли), его скорость распространения уменьшается, что приводит к ошибкам в измерении дальности. В современных GPS приёмниках используют различные алгоритмы (модели) для минимизации влияния этих задержек. Однако, используемые в настоящее время модели могут устранить только половину из возможной 70 нс задержки, что приводит к значительным (до 10 м) ошибкам в определении местоположения приемника. Ошибки спутниковых часов, неисправленные сегментом управления, могут приводить к ошибкам положения приемника порядка одного метра. Ошибки в эфемеридных данных обычно незначительны и тщательно отслеживаются со станций слежения, однако также могут приводить ошибкам в положении аппаратуры потребителя порядка 1 м. Многолучевая интерференция также вносит ошибки в определение местоположения с помощью GPS. Это происходит, когда сигнал отражается от объектов, расположенных на земной поверхности, что создаёт заметную интерференцию с сигналами приходящими непосредственно со спутников. Специальная техника обработки сигнала и продуманная конструкция антенн позволяет свести к минимуму этот источник ошибок. Однако при работе в городских условиях ошибки, вносимые многолучевой интерференцией, могут осложнить производство работ. Оценочное снижение точности в положении приемника из-за этого явления – порядка 0,5 м. До 1 мая 2000 года министерство обороны США использовало искусственное снижение точности спутникового сигнала для гражданских и неавторизированных пользователей – избирательный доступ (Selective Availability или S/A). Это приводило к тому, что точность полученных координат с помощью C/A-кода (30 метров) преднамеренно снижалась до 100 метров. Однако по решению президента США «Избирательный Доступ» был отключен. Кроме того, S/A можно исключить, применяя технику дифференциальной коррекции. Шум и систематические ошибки смещения, объединяясь, приводят к типичным ошибкам расстояния около пятнадцати метров для каждого из спутников. Геометрический фактор – геометрическое понижение точности GDOP (Geometric Dilution of Precision) Ошибки GPS изменяются в зависимости от взаимного расположения спутников, используемых в навигационном решении, и приемника. Объем фигуры, описанной единичными векторами от приемника до спутников, используемых в навигационном решении, обратно пропорционален параметру GDOP. Плохой GDOP (большое значение) – углы от приемника до множества используемых спутников одинаковы (рис. 17).
GDOP вычисляется из геометрических связей между положением приемника и положениями спутников, которые приемник использует для навигации, с использованием параметров из процесса навигационного решения. Ошибки дальностей до спутников умножаются на соответствующий коэффициент GDOP для оценки положения или ошибки времени. |
|

 . (14)
. (14)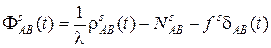 . (15)
. (15)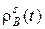 три координаты x, y, z пункта B, постоянное для спутника s и пунктов A и B целое число
три координаты x, y, z пункта B, постоянное для спутника s и пунктов A и B целое число 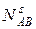 и новая для каждой новой эпохи измерений разность смещений часов
и новая для каждой новой эпохи измерений разность смещений часов 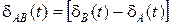 . Таким образом, число неизвестных равно 3 + ns + nt. При числе наблюдаемых спутников ns и числе эпох nt число уравнений разностей фаз будет равно nsnt. Чтобы число уравнений было не меньше числа неизвестных, должно выполняться неравенство nsnt ³ 3 + ns + nt, из которого следует, что число эпох измерений при наблюдении четырёх спутников должно быть не меньше, чем 3. А при использовании двух спутников - не меньше, чем 5.
. Таким образом, число неизвестных равно 3 + ns + nt. При числе наблюдаемых спутников ns и числе эпох nt число уравнений разностей фаз будет равно nsnt. Чтобы число уравнений было не меньше числа неизвестных, должно выполняться неравенство nsnt ³ 3 + ns + nt, из которого следует, что число эпох измерений при наблюдении четырёх спутников должно быть не меньше, чем 3. А при использовании двух спутников - не меньше, чем 5.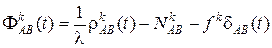 .
.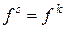 , запишем
, запишем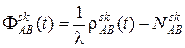 . (16)
. (16) ;
;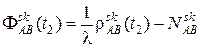 .
.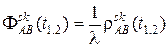 , (17)
, (17)

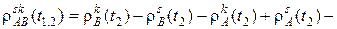
 .
.