|
|
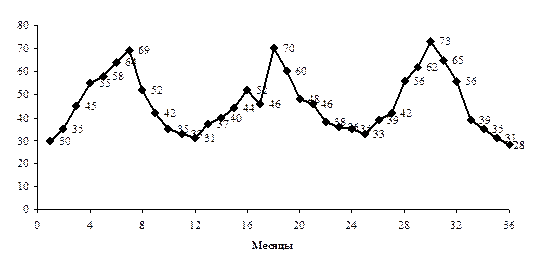
Оценка адекватности тренда и прогнозированиеДля найденного уравнения тренда необходимо провести оценку его надежности (адекватности), что осуществляется обычно с помощью критерия Фишера, сравнивая его расчетное значение Fр с теоретическим (табличным) значением FТ (Приложение 4). При этом расчетный критерий Фишера определяется по формуле (102):
где k – число параметров (членов) выбранного уравнения тренда. Для проверки правильности расчета сумм в формуле (102) можно использовать следующее равенство (103):
В нашем примере про ВО равенство (103) соблюдается (необходимые суммы рассчитаны в трех последних столбцах табл. 31): 89410,434 = 9652,171 + 79758,263. Сравнение расчетного и теоретического значений критерия Фишера ведется при заданном уровне значимости[32]с учетом степеней свободы: Проверим тренд на адекватность в нашем примере про ВО по формуле (102): FР = 79758,263*5/(9652,171*1) = 41,32 > FТ, значит, модель адекватна и ее можно использовать для прогнозирования (FТ = 6,61 находим по Приложению 4 в 1-ом столбце [ Как уже было отмечено ранее, в нашем примере про ВО России можно произвести выравнивание не только по прямой линии, но и по параболе, чего делать не будем, так как уже найденный линейный тренд адекватно описывает тенденцию[33]. При составлении прогнозов уровней социально-экономических явлений обычно оперируют не точечной, а интервальной оценкой, рассчитывая так называемые доверительные интервалы прогноза. Границы интервалов определяются по формуле (104):
где
Спрогнозируем ВО России на 2007 и 2008 годы с вероятностью 0,95 (значимостью 0,05), для чего найдем ошибку аппроксимации по формуле (105): Прогноз на 2007 и 2008 годы с вероятностью 0,95 по формуле (104): Y2007 = (257,671+53,371*4) Y2008 = (257,671+53,371*5) Как видно из полученных прогнозов, доверительный интервал достаточно широк (из-за достаточно большой величины ошибки аппроксимации). Более точный прогноз можно получить при выравнивании по параболе 2-го порядка[35]. Анализ сезонных колебаний В рядах динамики, уровни которых являются месячными или квартальными показателями, наряду со случайными колебаниями часто наблюдаются сезонные колебания, под которыми понимаются периодически повторяющиеся из года в год повышение и снижение уровней в отдельные месяцы или кварталы. Сезонным колебаниям подвержены внутригодовые уровни многих показателей. Например, расход электроэнергии в летние месяцы значительно меньше, чем в зимние; или рыночные цены на овощи в отдельные месяцы далеко не одинаковы. При графическом изображении таких рядов сезонные колебания проявляются в повышении и снижении уровней в определенные месяцы (кварталы). В качестве иллюстрации рядов с сезонными колебаниями могут служить данные, представленные в табл. 32 и их графическое изображение (рис. 15). Таблица 32. Динамика производства мороженого предприятием по месяцам, тонн
Рис. 15. Динамика производства мороженого предприятием по месяцам, тонн Вместо месячных показателей могут быть квартальные. Если колебания не случайны, то они сохраняются и в квартальных уровнях, как это показано в табл. 33 и на рис. 16, где месячные данные из табл. 32 преобразованы в квартальные. Таблица 33. Динамика производства мороженого предприятием по кварталам, тонн
Рис. 16. Динамика производства мороженого предприятием по кварталам, тонн Наблюдение за сезонными колебаниями позволяет устранить их там, где они нежелательны, а также решить ряд практических задач, например, определить потребности в сырье, рабочей силе в тех отраслях, где влияние сезонности велико. При изучении рядов динамики, содержащих «сезонную волну», ее выделяют из общей колеблемости уровней и измеряют. Существует 2 основных метода для решения этой задачи: расчет индексов сезонности и гармонический анализ. Индексы сезонности показывают, во сколько раз фактический уровень ряда в определенный момент или интервал времени t больше среднего уровня, либо уровня, вычисляемого по уравнению тренда (
где Yt – уровень ряда динамики за месяц (квартал) t;
Индексы сезонности желательно рассчитывать для рядов динамики, длиной в несколько лет, тогда формула индекса сезонности примет следующий вид:
где Например, по данным таблицы 32, представляющим ряд динамики за 3 года, индексы сезонности будем рассчитывать по формуле (107), для чего сначала рассчитаем При наличии тренда индексы сезонности определяются определяются аналогично по формулам (106) – (107) с учетом замены
Особое место при анализе сезонных колебаний занимает гармонический анализ сезонных колебаний, в котором осуществляется выравнивание ряда динамики с помощью ряда Фурье, уровни которого можно выразить как функцию времени следующим уравнением:
То есть сезонные колебания уровней динамического ряда можно представить в виде синусоидальных колебаний. Поскольку последние представляют собой гармонические колебания, то синусоиды, полученные при выравнивании по ряду Фурье, называют гармониками различных порядков (показатель k в этом уравнении определяет число гармоник). Обычно при выравнивании по ряду Фурье рассчитывают несколько гармоник (чаще не более 4) и затем уже определяют, с каким числом гармоник ряд Фурье наилучшим образом отражает изменения уровней ряда. При выравнивании по ряду Фурье периодические колебания уровней динамического ряда представлены в виде суммы нескольких синусоид (гармоник), наложенных друг на друга. Так, при k=1 ряд Фурье будет иметь вид
а при k=2, соответственно,
и так далее. Параметры уравнения теоретических уровней, определяемого рядом Фурье, находят, как и в других случаях, методом наименьших квадратов. Приведем без вывода формулы[36], используемые для исчисления параметров ряда Фурье:
Последовательные значения t обычно определяются от 0 с увеличением (приростом), равным Например, при n=10 временнЫе точки t можно записать следующим образом:
или (после сокращения): При n=12 значения t приведены в первой строке таблицы 34, а во второй и третьей строках определены значения sinkt и coskt для первой гармоники. Таблица 34. Значения sinkt и coskt для первой гармоники 12-ти уровнего ряда динамики
В таблице 35 приведены исходные данные (графы 1 и 2) и расчет показателей, необходимых для получения уравнений первой гармоники (k=1) по формуле (112). Таблица 35. Вспомогательные расчеты параметров ряда Фурье
Искомое уравнение первой гармоники имеет вид:
Рис. 17. Динамика производства мороженого предприятием, тонн Аналогично рассчитываются параметры уравнения с применением второй, третьей и т.д. гармоник[37], а затем выбирается наиболее адекватное уравнение, то есть с минимальной ошибкой аппроксимации. На основе подобранного уравнения по ряду Фурье можно прогнозировать (экстраполировать) развитие уровней ряда в будущем по формуле (104). Например, определим доверительные интервалы производства мороженого на январь 2007 года с вероятностью 0,95, для чего найдем ошибку аппроксимации по формуле (105): Методические указания По данным ФСГС сальдо внешней торговли (СВТ) России за период 2000-2006 гг. характеризуется рядом динамики, представленным в табл. 36. Таблица 36. Сальдо внешней торговли (СВТ) России за период 2000-2006 гг.
Проанализируем данный ряд динамики: выявим тенденцию и сделаем прогноз на 2007 и 2008 годы с вероятностью 0,95. Для большей наглядности представим данные табл. 36 на графике – рис. 18.
Рис. 18. Сальдо внешней торговли (СВТ) России за период 2000-2006 гг. Данные табл. 36 и рис. 18 наглядно иллюстрируют постепенное уменьшение и последующий рост СВТ России за период 2000-2006 гг.. Очевидно, что такую динамику не следует описывать линейной функцией тренда. Попробуем описать эту динамику с помощью тренда по параболе 2-го порядка по формуле (92). Параметры параболы (a0, a1, a2) определим методом МНК, для чего в формуле (99) вместо В соответствии с вышеизложенным найдем частные производные:
Сократив каждое уравнение на 2, раскрыв скобки и перенеся члены с y в правую сторону, а остальные – оставив в левой, получим систему нормальных уравнений:
Упростим систему (113), введя условную нумерацию t от середины ряда. Тогда ∑t = 0 и ∑t3 = 0, а система (113) упростится до следующего вида:
Решая систему (114) [38], находим параметры a0, a1, a2:
Определим по формулам (115) – (117) параметры уравнения параболы для нашего примера про СВТ России, для чего исходные данные и все расчеты необходимых сумм представим в табл. 37. Таблица 37. Вспомогательные расчеты для параболического тренда
Из табл. 37 получаем по формулам (115) – (117): a0 = 62,357, a1 = 15,061 и a2 = 4,382. Отсюда искомое уравнение тренда
Рис. 19. Эмпирические и трендовые уровни СВТ России Анализируя рис. 19, то есть сравнивая эмпирические и теоретические уровни, отмечаем, что они почти полностью совпадают, значит парабола 2-го порядка – вполне адекватная функция для отражения основной тенденции (тренда) СВТ России за 2000-2006 годы. Равенство (103) соблюдается (необходимые суммы рассчитаны в трех последних столбцах табл. 37): 8138,249 = 174,079 + 7964,23. Теперь проверим тренд на адекватность по формуле (102): FР = 7964,23*4/(174,079*2) = 91,5 > FТ, значит модель адекватна и ее можно использовать для прогнозирования (FТ = 6,94 находим по Приложению 4 в 2-ом столбце [ Спрогнозируем СВТ России на 2007 и 2008 годы с вероятностью 0,95, для чего найдем ошибку аппроксимации по формуле (105): Прогноз СВТ России на 2007 и 2008 годы с вероятностью 0,95 по формуле (104): Y2007 = (62,357+15,061*4+4,382*42) Y2008 = (62,357+15,061*5+4,382*52) Как видно из полученных прогнозов, доверительный интервал достаточно узок, значит получен достаточно точный прогноз СВТ России на 2006 и 2007 годы. Его надежная оценка имеет принципиальное значение для макроэкономического анализа и прогнозирования, поскольку его величина влияет на общую картину платежного баланса. Так, недооценка положительного сальдо означает недооценку отрицательного сальдо потоков капитала, и наоборот. В то же время потоки капитала увязаны с динамикой внутренних сбережений, что имеет принципиально важное значение для анализа инвестиционного потенциала и прогнозирования инвестиционной активности. 6.8. Контрольные задания Проанализировать ряд динамики, приведенный в таблице 38 (по данным ФСГС), сделать прогноз на 2007 год. Таблица 38. Варианты выполнения контрольного задания |
|
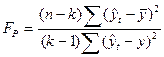 , (102)
, (102) . (103)
. (103)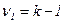 и
и  . При условии Fр > FТ считается, что выбранная математическая модель ряда динамики адекватно отражает обнаруженный в нем тренд.
. При условии Fр > FТ считается, что выбранная математическая модель ряда динамики адекватно отражает обнаруженный в нем тренд. = k – 1 = 2 – 1 = 1] и 5-й строке [
= k – 1 = 2 – 1 = 1] и 5-й строке [  = n – k = 5]).
= n – k = 5]). , (104)
, (104) – точечный прогноз, рассчитанный по модели тренда;
– точечный прогноз, рассчитанный по модели тренда;  – коэффициент доверия по распределению Стьюдента при уровне значимости
– коэффициент доверия по распределению Стьюдента при уровне значимости  и числе степеней свободы
и числе степеней свободы  =n–1 (Приложение 2)[34];
=n–1 (Приложение 2)[34];  – ошибка аппроксимации, определяемая по формуле (105):
– ошибка аппроксимации, определяемая по формуле (105): . (105)
. (105) =
= 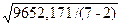 = 43,937 и найдем коэффициент доверия по распределению Стьюдента по Приложению 2:
= 43,937 и найдем коэффициент доверия по распределению Стьюдента по Приложению 2: 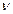 = 7 – 1= 6.
= 7 – 1= 6. 2,4469*43,937 или 363,6<Y2007<578,7 (млрд. долл.);
2,4469*43,937 или 363,6<Y2007<578,7 (млрд. долл.);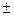 2,4469*43,937 или 417,0<Y2008<632,0 (млрд. долл.).
2,4469*43,937 или 417,0<Y2008<632,0 (млрд. долл.).


 , (106)
, (106) – средний уровень всего ряда динамики.
– средний уровень всего ряда динамики. , (107)
, (107) – средний уровень ряда динамики по одноименным месяцам t за T лет.
– средний уровень ряда динамики по одноименным месяцам t за T лет. (4-я строка таблицы 32), а затем, разделив полученные значение на T=3, получим средние уровни за каждый месяц
(4-я строка таблицы 32), а затем, разделив полученные значение на T=3, получим средние уровни за каждый месяц  (5-я строка таблицы 32). Средний уровень всего ряда определяем по формуле средней арифметической простой:
(5-я строка таблицы 32). Средний уровень всего ряда определяем по формуле средней арифметической простой:  . В 6-й строке таблицы 32 определены индексы сезонности для каждого месяца по формуле (107), то есть делением значений в 5-й строке на 46,111.
. В 6-й строке таблицы 32 определены индексы сезонности для каждого месяца по формуле (107), то есть делением значений в 5-й строке на 46,111. . (108)
. (108) . (109)
. (109) , (110)
, (110) (111)
(111)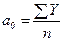 ;
;  ;
;  . (112)
. (112) , где n – число уровней эмпирического ряда.
, где n – число уровней эмпирического ряда.





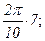

 ,
,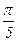 ;
;  ;
; 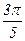 ;
; 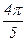 ;
;  ;
;  ;
;  ;
;  ;
;  .
.


 = 4,727 и определим коэффициент доверия по нормальному распределению (так как число уровней n>30) по Приложению 1: t = 1,96. Тогда прогноз на январь 2007 года с вероятностью 0,95 по формуле (104): Yянв07 = 31,71
= 4,727 и определим коэффициент доверия по нормальному распределению (так как число уровней n>30) по Приложению 1: t = 1,96. Тогда прогноз на январь 2007 года с вероятностью 0,95 по формуле (104): Yянв07 = 31,71 
 . Тогда
. Тогда  . Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значении a0, a1, a2 функция трех переменных S может достигнуть минимума. Как известно, для этого надо найти частные производные S по a0, a1, a2 и приравнять их к нулю и после элементарных преобразований решить систему трех уравнений с тремя неизвестными.
. Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значении a0, a1, a2 функция трех переменных S может достигнуть минимума. Как известно, для этого надо найти частные производные S по a0, a1, a2 и приравнять их к нулю и после элементарных преобразований решить систему трех уравнений с тремя неизвестными.
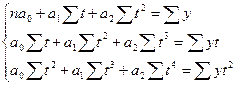 (113)
(113) (114)
(114) (115)
(115)  (116)
(116)  (117)
(117)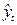




 = 6,597 и найдем коэффициент доверия по распределению Стьюдента по Приложению 2:
= 6,597 и найдем коэффициент доверия по распределению Стьюдента по Приложению 2: