|
|
УЧЕБНЫЕ МАТЕРИАЛЫ ПО РАЗДЕЛАМ КУРСАФИЗИКИ I. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ, МОЛЕКУЛЯНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ Пояснения к рабочей программе
Приступая к изучению физики, необходимо уяснить, что физика, наряду с другими естественными науками, изучает объективные свойства окружающего нас материального мира. Она исследует наиболее общие формы движения материи и их взаимные превращения. Движение есть форма существования материи. Физические понятия являются простейшими и в то же время основополагающими и всеобщими в естествознании (пространство, время, движение, масса, работа, энергия и др.). Изучать основы классической механики надо исходя из представлений современной физики, в которой основные понятия классической механики не утратили своего значения, а получили дальнейшее развитие, обобщение и критическую оценку с точки зрения их применения. Следует помнить, что механика – это наука о простейших формах движения материальных тел и происходящих при этом взаимодействиях между телами. Движение всегда существует в пространстве и во времени. Диалектический материализм учит, что пространство, поле и время являются основными формами существования материи. Предметом классической механики является движение макроскопических материальных тел, совершаемое со скоростями, малыми по сравнению со скоростью света в вакууме. Движение частиц со скоростями порядка скорости света рассматривается в теории относительности, а движение микрочастиц изучается в квантовой механике. В контрольную работу № 1 включены задачи, дающие возможность проверить знания студентов по ключевым вопросам классической механики и элементам специальной теории относительности. Решая задачи по кинематике, в которых необходимо использовать математический аппарат дифференциального и интегрального исчислений, студент должен научиться определять мгновенные скорость и ускорение по заданной зависимости координаты от времени, а так же решать обратные задачи. Задачи на динамику материальной точки и поступательное движение твердого тела охватывают такие вопросы, как закон движения центра масс механической системы, закон сохранения количества движения, работа силы и ее выражение через криволинейный интеграл, связь кинетической энергии механической системы с работой сил, приложенных к этой системе, закон сохранения механической энергии. Тщательного изучения и понимания требуют вопросы о поле как форме материи, осуществляющей взаимодействие между частицами вещества или телами, о потенциальной энергии механической системы. В задачах на кинематику и динамику вращательного движения твердого тела главное внимание уделялось изучению соотношений между линейными и угловыми характеристиками, понятий момента силы, момента инерции тела, законов сохранения количества движения, момента количества движения и механической энергии. В контрольную работу включены задачи по элементам специальной теории относительности, которые охватывают следующие вопросы: относительность одновременности, длин и промежутков времени, релятивистский закон сложения скоростей, зависимость релятивистской массы от скорости, соотношение между релятивистской массой и полной энергией. Решая эти задачи, студент должен усвоить, что законы классической механики имеют границы применимости и что они получаются как следствие теории относительности. Изучая физические основы молекулярной физики и термодинамики, студенты должны уяснить, что существуют два качественно различных и взаимодополняющих метода исследования физических свойств макроскопических систем – статистический (молекулярно-кинетический) и термодинамический. Молекулярно-кинетический метод исследования лежит в основе молекулярной физики, термодинамический – в основе термодинамики. Молекулярно-кинетическая теория позволяет с единой точки зрения рассмотреть различные явления во всех состояниях вещества, вскрыть их физическую сущность и теоретическим путем вывести многочисленные закономерности, открытые экспериментально и имеющие большое практическое значение. При изучении молекулярно-кинетической теории следует уяснить, что свойства огромной совокупности молекул отличны от свойств каждой отдельной молекулы и свойства макроскопической системы в конечном счете определяются свойствами частиц системы, особенностями их движения и средними значениями кинематических характеристик частиц, т. е. их скоростей, энергий т. д. В отличие от молекулярно-кинетической теории, термодинамика не изучает конкретно молекулярные взаимодействия, происходящие с отдельными атомами или молекулами, а рассматривает взаимопревращения и связь различных видов энергии, теплоты и работы. Термодинамика базируется на опытных законах (началах), которые позволяют описывать физические явления, связанные с превращением энергии макроскопическим путем. При изучении основ термодинамики студент должен четко усвоить такие понятия, как термодинамическая система, термодинамические параметры (параметры состояния), равновесное состояние, уравнение состояния, термодинамический процесс, внутренняя энергия, энтропия и т. д. Задачи контрольной работы дают возможность проверить знания студентов по основным вопросам молекулярной физики и термодинамики. В задачах на тему «Основы молекулярно-кинетической теории» внимание уделено таким вопросам программы, как уравнение Клайперона-Менделеева, уравнение молекулярно-кинетической теории, средние кинетические энергии поступательного и вращательного движения молекул, средняя длина свободного пробега и среднее число соударений, явления переноса. Задачи по теме «Основы термодинамики» охватывают такие важные соотношения и понятия, как первое начало термодинамики, внутренняя энергия, работа при различных изопроцессах и адиабатном процессе. Включены также задачи, которые позволяют проверить понимание второго начала термодинамики, понятие энтропия идеального газа, являющегося, в отличие от количества теплоты функцией состояния. Задачи в контрольной работе расположены приблизительно в том порядке, в каком соответствующие вопросы рассматриваются в рабочей программе. ОСНОВНЫЕ ФОРМУЛЫ МЕХАНИКА Мгновенная скорость: где Ускорение: тангенциальное: нормальное: полное: где R – радиус кривизны траектории, Угловая скорость: где Ускорение угловое: Связь между линейными и угловыми величинами: Импульс (количество движения) материальной точки: где m – масса материальной точки. Основное уравнение динамики материальной точки (II закон Ньютона):
Закон сохранения импульса для изолированной системы: Радиус-вектор центра масс: Скорости частиц после столкновения: Сила сухого трения: где f – коэффициент трения, Сила упругости: где k – коэффициент упругости (жесткость), Сила гравитационного взаимодействия: где m1 и m2 – массы частиц, g – гравитационная постоянная, r – расстояние между частицами. Работа силы: Мощность: Потенциальная энергия: упругодеформированного тела: гравитационного взаимодействия двух частиц: тела в однородном гравитационном поле: где g – ускорение свободного падения,h – расстояние от нулевого уровня. Потенциал гравитационного поля Земли: где M3 – масса Земли, R3 – радиус Земли, h – расстояние от поверхности Земли. Напряженность гравитационного поля Земли: Кинетическая энергия материальной точки: Закон сохранения механической энергии: Момент инерции материальной точки: момент инерции абсолютно твердого тела: где r – расстояние до оси вращения. Моменты инерции тел массой m относительно оси, проходящей через центр масс: тонкостенного цилиндра, кольца радиуса R, если ось вращения совпадает с осью цилиндра: сплошного цилиндра, диска радиуса R, если ось вращения совпадает с осью цилиндра: шара радиуса R: тонкого стержня длиной l, если ось вращения перпендикулярна стержню: Момент инерции тела массой m относительно произвольной оси (теорема Штейнера): где Jo – момент инерции относительно параллельной оси, проходящей через центр масс тела, d – расстояние между осями. Момент силы: где Момент импульса: Основное уравнение динамикивращательного движения: Закон сохранения момента импульса для изолированной системы: Работа при вращательном движении: Кинетическая энергия вращающегося тела: Релятивистское изменение длины: где l0 – длина покоящегося тела, с – скорость света в вакууме. Релятивистское замедление времени: гдеt0 –собственное время. Релятивистская масса: где m0 – масса покоя. Энергия покоя частицы: Полная энергия релятивистской частицы: Релятивистский импульс: Кинетическая энергия релятивистской частицы: Релятивистское соотношение между полной энергией и импульсом: Теорема сложения скоростей в релятивистской механике: где u и МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА Количество вещества: где N – число молекул, NA – постоянная Авогадро, m – масса вещества, m – молярная масса. Уравнение Клайперона-Менделеева: где P – давление газа, V – его объем, R – малярная газовая постоянная, T – абсолютная температура. Уравнение молекулярно-кинетической теории газа: где n – концентрация молекул, Средняя энергия молекулы: где i – число степеней свободы, k – постоянная Больцмана. Внутренняя энергия идеального газа: Скорости молекул: средняя квадратичная: средняя арифметическая: наиболее вероятная: Средняя длина свободного пробега молекулы: где d – эффективный диаметр молекулы. Среднее число столкновений молекулы в единицу времени:
Распределение молекул в потенциальном поле сил: где П – потенциальная энергия молекулы. Барометрическая формула: Уравнение диффузии: где D – коэффициент диффузии, r – плотность, dS – элементарная площадка, перпендикулярная к направлению вдоль которого происходит диффузия. Уравнение теплопроводности: где æ – теплопроводность. Сила внутреннего трения: где h – динамическая вязкость. Коэффициент диффузии: Вязкость (динамическая): Теплопроводность: æ где СV – удельная изохорная теплоемкость. Молярная теплоемкость идеального газа: изохорная: изобарная: Первое начало термодинамики: Работа расширения газа при процессе: изобарном: изотермическом: изохорном: адиабатном: где Уравнения Пуассона: Коэффициент полезного действия цикла Карно: где Q и T – количество теплоты, полученное от нагревателя, и его температура; Q0 и Т0 – количество теплоты, переданное холодильнику, и его температура. Изменение энтропии при переходе из состояния 1в состояние 2: ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1.Движение тела массой 1 кг задано уравнением s = 6t3 + 3t + 2. Найти зависимость скорости и ускорения от времени. Вычислить силу, действующую на тело в конце второй секунды. Решение. Мгновенную скорость находим как производную от пути по времени: Ответ: 2. Стержень длиной 1 м движется мимо наблюдателя со скоростью на 20% меньше скорости света. Какой покажется наблюдателю его длина? Решение. Зависимость длины тела от скорости в релятивистской механике выражается формулой: Ответ: l = 0,6 м. 3. Две частицы движутся навстречу друг другу со скоростями: 1) Решение. Согласно теореме о сложении скоростей тел, движущихся навстречу друг другу, в теории относительности:
Это подтверждает, что, во-первых, ни в какой инерциальной системе отсчета скорость процесса не может превзойти скорость света, и, во-вторых, скорость распространения света в вакууме абсолютна. Ответ: 4. На двух шнурах одинаковой длины, равной 0,8 м, подвешены два свинцовых шара массами 0,5 и 1 кг. Шары соприкасаются между собой. Шар меньшей массы отвели в сторону так, что шнур отклонился на угол a=60°, и отпустили. На какую высоту поднимутся оба шара после столкновения? Удар считать центральным и неупругим. Определить энергию, израсходованную на деформацию шаров при ударе. Решение. Так как удар шаров неупругий, то после удара шары будут двигаться с общей скоростью u. Закон сохранения количества движения при этом ударе имеет вид:
Здесь
Из уравнений (1) и (2) находим скорость шаров после удара:
Кинетическая энергия, которой обладают шары после удара, переходит в потенциальную:
где h – высота поднятия шаров после столкновения. Из формулы (4) находим
Ответ: h = 0,044 м, DEД = 1,3 Дж. 5.Молот массой 70 кг падает с высоты 5 м и ударяет по железному изделию, лежащему на наковальне. Масса наковальни вместе с изделием 1330 кг. Считая удар абсолютно неупругим, определить энергию, расходуемую на деформацию изделия. Систему молот–изделие–наковальня считать замкнутой. Решение. По условию задачи, система молот–изделие–наковальня считается замкнутой, а удар неупругий. На основании закона сохранения энергии можно считать, что энергия, затраченная на деформацию изделия, равна разности значений механической энергии системы до и после удара. Считаем, что во время удара изменяется только кинетическая энергия тел, т. е. незначительным перемещением тел по вертикали во время удара пренебрегаем. Тогда для энергии деформации изделия имеем:
где
Общую скорость всех тел системы после неупругого удара найдем, применив закон сохранения количества движения:
Подставив в формулу (1) выражения (2) и (3), получим: Ответ: 6. Тело массой 1 кг под действием постоянной силы движется прямолинейно. Зависимость пути, пройденного телом, от времени задана уравнением s = 2t2+4t+1. Определить работу силы за 10 сек от начала ее действия и зависимость кинетической энергии от времени. Решение. Работа, совершаемая силой, выражается через криволинейный интеграл:
Сила, действующая на тело, из II закона Ньютона равна:
Из выражения (2) определим ds:
Подставив (4) и (5) в уравнение (1), получим:
Подставляя (2) в (6), имеем: Ответ: А = 960 Дж, Т = m(8t2+16t+8). 7. Протон движется со скоростью 0,7с (с – скорость света). Найти количество движения и кинетическую энергию протона. Решение. Количество движения протона определяется по формуле:
Так как скорость протона сравнима со скоростью света, то необходимо учесть зависимость массы от скорости, воспользовавшись релятивистским выражением для массы:
где m – масса движущегося протона; m0 =1,67×10-27 кг – масса покоя протона; v – скорость движения протона; c = 3×108 м/с – скорость света в вакууме; v/c = b – скорость протона, выраженная в долях скорости света. Подставляя уравнение (2) в (1) получаем:
Ответ: p = 4,91×10-19 кг×м/с, Т = 0,6×10-10 Дж. 8. Тонкий стержень вращается с угловой скоростью 10 с-1 в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. В процессе вращения в той же плоскости стержень перемещается так, что ось вращения проходит через его конец. Найти угловую скорость после перемещения. Решение. Используем закон сохранения момента импульса:
Известно, что момент инерции стержня относительно оси, проходящей через центр масс и перпендикулярной стержню, равен:
По теореме Штейнера:
Подставляя, формулы (2) и (3) в (1), имеем: Ответ: w2 = 2,5 c-1. 9. Маховик массой 4 кг вращается с частотой 720 мин-1 вокруг горизонтальной оси, проходящей через его центр. Массу маховика можно считать равномерно распределенной по его ободу радиусом 40 см. Через 30 с под действием тормозящего момента маховик остановился. Найти тормозящий момент и число оборотов, которое сделает маховик до полной остановки. Решение. Для определения тормозящего момента М сил, действующих на тело, нужно применить основное уравнение динамики вращательного движения:
где J – момент инерции маховика относительно оси, проходящей через центр масс; Угол поворота (т. е. угловой путь
где Ответ: М = 1,61 Н×м, N = 180. 10. В сосуде объемом 2 м3 находится смесь 4 кг гелия и 2 кг водорода при температуре 27 °С. Определить давление и молярную массу смеси газов. Решение. Воспользуемся уравнением Клайперона-Менделеева, применив его к гелию и водороду:
где P1 – парциальное давление гелия; m1 – масса гелия;
Из уравнения (1) и (2) выразим P1 и P2 и подставим в уравнение (3). Имеем:
Молярную массу смеси газов найдем по формуле: Ответ: P = 2493 КПа, 11. Чему равны средние кинетические энергии поступательного и вращательного движения молекул, содержащихся в 2 кг водорода при температуре 400 К? Решение. Считаем водород идеальным газом. Молекула водорода двухатомная, связь между атомами считаем жесткой. Тогда число степеней свободы молекулы водорода равно 5, три из которых поступательные и две вращательные. В среднем на одну степень свободы приходится энергия Ответ: 12. Определить среднюю длину свободного пробега молекул и число соударений за 1 с, происходящих между всеми молекулами кислорода, находящегося в сосуде емкостью 2 л при температуре 27 0С и давлении 100 кПа. Решение. Средняя длина свободного пробега молекул кислорода вычисляется по формуле: Ответ: Z = 9×1028 с-1, 13. Определить коэффициенты диффузии и внутреннего трения азота, находящегося при температуре Т = 300 К и давлении 105 Па. Решение. Коэффициент диффузии определяется по формуле: Ответ: D = 4,7×105 м2/с и h = 5,23×10-5 кг/(м×с). 14. Кислород массой 160 г нагревают при постоянном давлении от 320 до 340 К. Определить количество теплоты, поглощенное газом, изменение внутренней энергии и работу расширения газа. |
|
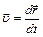 ,
, – радиус-вектор материальной точки, t – время.
– радиус-вектор материальной точки, t – время. ,
, ,
,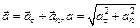 ,
, – единичный вектор нормали, направленный к центру кривизны траектории.
– единичный вектор нормали, направленный к центру кривизны траектории.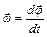 ,
,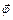 - угловое перемещение.
- угловое перемещение.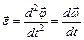 .
.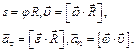
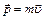 ,
,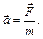
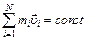 .
.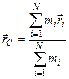 .
.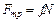 ,
,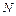 – сила нормального давления.
– сила нормального давления. ,
,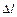 – деформация.
– деформация. ,
,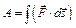 .
.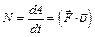 .
.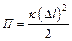 ,
,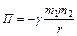 ,
, ,
, ,
,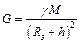 .
.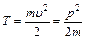 .
.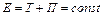 .
.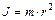 ,
, ,
,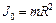 ,
,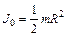 ,
,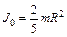 ,
,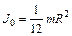 .
.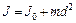 ,
,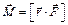 ,
,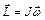 .
. .
.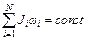 .
.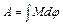 .
.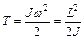 .
.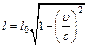 ,
,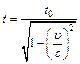 ,
,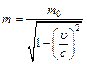 ,
, .
.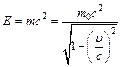 .
.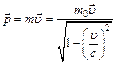 .
.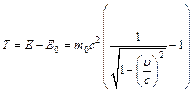 .
.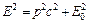 .
.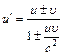 ,
,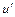 – скорости в двух инерциальных системах отсчета, движущихся относительно друг друга со скоростью
– скорости в двух инерциальных системах отсчета, движущихся относительно друг друга со скоростью  , совпадающей по направлению с u (знак «-») или противоположно ей направленной (знак «+»).
, совпадающей по направлению с u (знак «-») или противоположно ей направленной (знак «+»). ,
, ,
, ,
, – средняя кинетическая энергия поступательного движения молекулы, m0 – масса молекулы,
– средняя кинетическая энергия поступательного движения молекулы, m0 – масса молекулы, 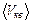 – средняя квадратичная скорость.
– средняя квадратичная скорость.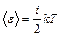 ,
, .
.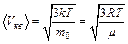 ,
,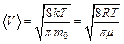 ,
, .
. ,
,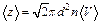 .
.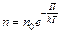 ,
,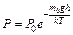 .
.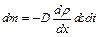 ,
,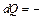 , æ
, æ 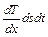 ,
,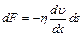 ,
,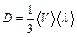 .
.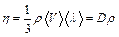 .
. ,
,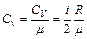 ,
,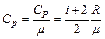 .
.
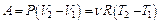 ,
,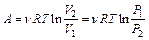 ,
,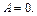
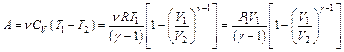 ,
,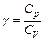 .
.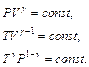
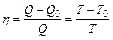 ,
,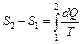 .
.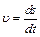 ,
, 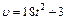 . Мгновенное ускорение определяется первой производной от скорости по времени или второй производной от пути по времени:
. Мгновенное ускорение определяется первой производной от скорости по времени или второй производной от пути по времени: 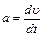 ,
, 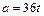 . Сила, действующая на тело, определяется по второму закону Ньютона:
. Сила, действующая на тело, определяется по второму закону Ньютона: 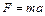 , где
, где  , согласно условию задачи, ускорение в конце второй секунды. Тогда
, согласно условию задачи, ускорение в конце второй секунды. Тогда 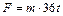 ,
, 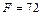 Н.
Н.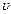 = с и u = 0,75с. Найти их относительную скорость в первом и втором случаях.
= с и u = 0,75с. Найти их относительную скорость в первом и втором случаях.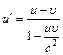 , где
, где 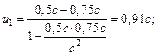
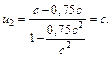
 = 0,91с;
= 0,91с; 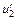 = с.
= с.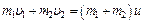 . (1)
. (1)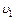 и
и 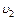 – скорости шаров до удара. Скорость большого шара до удара равна нулю (
– скорости шаров до удара. Скорость большого шара до удара равна нулю (  ему сообщается потенциальная энергия, которая затем переходит в кинетическую:
ему сообщается потенциальная энергия, которая затем переходит в кинетическую: 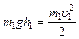 . Следовательно:
. Следовательно: 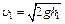 . Из геометрических построений следует:
. Из геометрических построений следует: 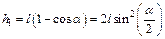 , поэтому:
, поэтому: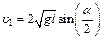 . (2)
. (2)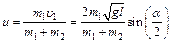 . (3)
. (3)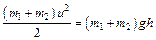 , (4)
, (4)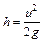 ,или с учетом (3)
,или с учетом (3)  и подставив числовые данные получим h = 0,044 м. При неупругом ударе шаров часть энергии расходуется на их деформацию. Энергия деформации определяется разностью кинетических энергий до и после удара:
и подставив числовые данные получим h = 0,044 м. При неупругом ударе шаров часть энергии расходуется на их деформацию. Энергия деформации определяется разностью кинетических энергий до и после удара: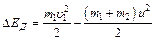 . Используя уравнения (2) и (3), получаем:
. Используя уравнения (2) и (3), получаем:  ,
, 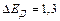 Дж.
Дж.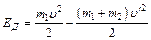 , (1)
, (1)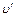 – общая скорость всех тел системы после неупругого удара. Скорость молота в конце падения с высоты h определяется без учета сопротивления воздуха и трения по формуле:
– общая скорость всех тел системы после неупругого удара. Скорость молота в конце падения с высоты h определяется без учета сопротивления воздуха и трения по формуле: . (2)
. (2)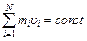 . Для рассматриваемой системы закон сохранения количества движения имеет вид
. Для рассматриваемой системы закон сохранения количества движения имеет вид  , откуда:
, откуда: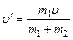 . (3)
. (3)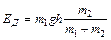 ,
, 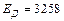 Дж.
Дж.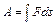 . (1)
. (1)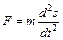 (мгновенное значение ускорения определяется первой производной от скорости по времени или второй производной от пути по времени). В соответствии с этим находим:
(мгновенное значение ускорения определяется первой производной от скорости по времени или второй производной от пути по времени). В соответствии с этим находим: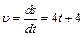 , (2),
, (2), 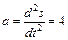 , (3)
, (3)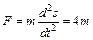 . (4)
. (4)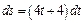 (5)
(5)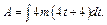 По этой формуле определим работу, совершаемую силой за 10 сек от начала ее действия:
По этой формуле определим работу, совершаемую силой за 10 сек от начала ее действия:  , А = 960 Дж. Кинетическая энергия определяется по формуле:
, А = 960 Дж. Кинетическая энергия определяется по формуле: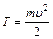 . (6)
. (6)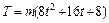 .
.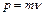 . (1)
. (1)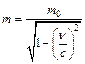 , (2)
, (2)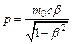 ,
, 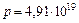 кг×м/с. В релятивистской механике кинетическая энергия частицы определяется как разность между полной энергией Е и энергией покоя Е0 этой частицы:
кг×м/с. В релятивистской механике кинетическая энергия частицы определяется как разность между полной энергией Е и энергией покоя Е0 этой частицы: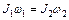 . (1)
. (1)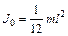 . (2)
. (2) . (3)
. (3)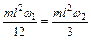 , откуда
, откуда 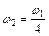 .
.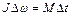 , (1)
, (1)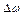 – изменение угловой скорости за промежуток времени
– изменение угловой скорости за промежуток времени 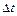 . По условию,
. По условию, 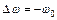 , где
, где 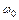 – начальная угловая скорость, так как конечная угловая скорость
– начальная угловая скорость, так как конечная угловая скорость 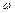 = 0. Выразим начальную угловую скорость через частоту вращения маховика; тогда
= 0. Выразим начальную угловую скорость через частоту вращения маховика; тогда 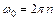 и
и 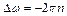 Момент инерции маховика
Момент инерции маховика 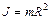 , где m – масса маховика; R – его радиус. Формула (1) принимает вид:
, где m – масса маховика; R – его радиус. Формула (1) принимает вид: 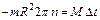 откуда М = -1,61 Н×м. Знак «-» говорит о том, что момент томозящий.
откуда М = -1,61 Н×м. Знак «-» говорит о том, что момент томозящий.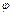 ) за время вращения маховика до остановки может быть определен по формуле для равнозамедленного вращения:
) за время вращения маховика до остановки может быть определен по формуле для равнозамедленного вращения: , (2)
, (2) – угловое ускорение. По условию,
– угловое ускорение. По условию, 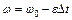 ,
, 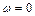 ,
, 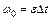 . Тогда выражение (2) можно записать так:
. Тогда выражение (2) можно записать так: 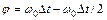 . Так как j = 2pN, w0 = 2pn, то число полных оборотов маховика:
. Так как j = 2pN, w0 = 2pn, то число полных оборотов маховика: 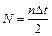 .
.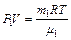 , (1)
, (1)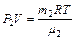 , (2)
, (2)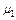 – его молярная масса; V – объем сосуда; Т – температура газа; R = 8,31 Дж/(моль×К) – молярная газовая постоянная; P2 - парциальное давление водорода; m2 – масса водорода;
– его молярная масса; V – объем сосуда; Т – температура газа; R = 8,31 Дж/(моль×К) – молярная газовая постоянная; P2 - парциальное давление водорода; m2 – масса водорода; 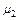 – его молярная масса. Под парциальным давлением P1 и P2 понимается то давление, которое производил бы газ, если бы он находился в сосуде один. По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси:
– его молярная масса. Под парциальным давлением P1 и P2 понимается то давление, которое производил бы газ, если бы он находился в сосуде один. По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси: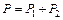 . (3)
. (3)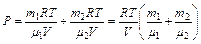 . (4)
. (4)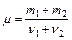 , где v1 и v2 – число молей гелия и водорода соответственно. Число молей газов определим по формулам:
, где v1 и v2 – число молей гелия и водорода соответственно. Число молей газов определим по формулам: 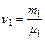 и
и 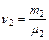 . Тогда:
. Тогда: 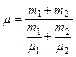 . Подставляя числовые значения получаем: P = 2493 КПа и
. Подставляя числовые значения получаем: P = 2493 КПа и 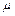 = 3×10-3 кг/моль.
= 3×10-3 кг/моль.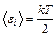 , где k – постоянная Больцмана; Т – термодинамическая температура. Для одной молекулы:
, где k – постоянная Больцмана; Т – термодинамическая температура. Для одной молекулы: 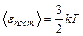 и
и 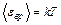 . Число молекул, содержащихся в массе газа:
. Число молекул, содержащихся в массе газа: 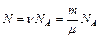 . Тогда средняя кинетическая энергия поступательного движения молекул двух килограмм водорода:
. Тогда средняя кинетическая энергия поступательного движения молекул двух килограмм водорода: 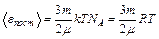 . Средняя кинетическая энергия вращательного движения этих же молекул:
. Средняя кинетическая энергия вращательного движения этих же молекул: 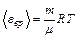 . Подставляя числовые значения имеем:
. Подставляя числовые значения имеем: 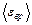 =2324 КДж.
=2324 КДж.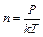 , где k – постоянная Больцмана. Таким образом, имеем:
, где k – постоянная Больцмана. Таким образом, имеем: 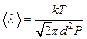 . Число соударений Z, происходящих между всеми молекулами за 1 с, равно:
. Число соударений Z, происходящих между всеми молекулами за 1 с, равно: 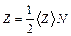 , где N – число молекул кислорода в сосуде объемом 2×10-3 м3; <Z> – среднее число соударений одной молекулы за 1 с. Число молекул в сосуде:
, где N – число молекул кислорода в сосуде объемом 2×10-3 м3; <Z> – среднее число соударений одной молекулы за 1 с. Число молекул в сосуде: 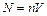 . Среднее число соударений молекулы за 1 с равно:
. Среднее число соударений молекулы за 1 с равно:  , где <V> – средняя арифметическая скорость молекулы. Тогда выражение для Z перепишется как:
, где <V> – средняя арифметическая скорость молекулы. Тогда выражение для Z перепишется как: 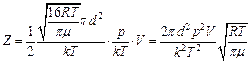 . Подставляя числовые значения, получим: Z = 9×1028 с-1,
. Подставляя числовые значения, получим: Z = 9×1028 с-1,  = 3,56×108 м.
= 3,56×108 м.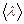 воспользуемся формулой из решения примера 12:
воспользуемся формулой из решения примера 12: 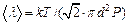 . Выражение для коэффициента диффузии примет вид:
. Выражение для коэффициента диффузии примет вид: 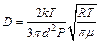 . Коэффициент внутреннего трения:
. Коэффициент внутреннего трения: 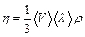 , где r – плотность газа при температуре 300 К и давлении 105 Па. Для нахождения r воспользуемся уравнением состояния идеального газа. Запишем его для двух состояний азота: при нормальных условиях Т0=273 К, P=1,01×105 Па и в условиях задачи:
, где r – плотность газа при температуре 300 К и давлении 105 Па. Для нахождения r воспользуемся уравнением состояния идеального газа. Запишем его для двух состояний азота: при нормальных условиях Т0=273 К, P=1,01×105 Па и в условиях задачи: 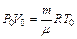 и
и 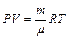 . Учитывая, что
. Учитывая, что 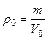 и
и  , имеем:
, имеем: 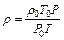 . Коэффициент внутреннего трения газа может быть выражен через коэффициент диффузии:
. Коэффициент внутреннего трения газа может быть выражен через коэффициент диффузии: 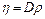 . Подставляя числовые значения, получим: D = 4,7×105 м2/с и h = 5,23×10-5 кг/(м×с).
. Подставляя числовые значения, получим: D = 4,7×105 м2/с и h = 5,23×10-5 кг/(м×с).