|
|
Пояснения к рабочей программе
Изучение электрических и магнитных явлений было впервые обощено в XIX в. Эти явления связаны с особой формой существования материи – электромагнитным полем. Электромагнитные взаимодействия не только объясняют все электромагнитные явления, но и обеспечивают силы, обусловливающие существование вещества на атомном и молекулярном уровнях как целого. Важность теории электромагнитного поля связана с тем, что она включает всю оптику, так как свет представляет собой электромагнитное излучение. Основой теории электромагнитного поля является теория Максвелла. Уравнения Максвелла установили тесную связь между электрическими и магнитными явлениями, которые раньше рассматривались как независимые. Максвелл сформулировал такое важнейшее понятие физики, как электромагнитное поле. Изучение основ электродинамики начинается с электрического поля в вакууме. Эта тема является фундаментом раздела, включающего электростатику и постоянный ток. Особое внимание при изучении этого раздела следует обратить на закон сохранения электрического заряда, инвариантность его в теории относительности, на силовую и энергетическую характеристики поля (напряженность, потенциал) и связь между ними. Студент должен уметь применять теорему Остроградского-Гаусса для вычисления напряженности электрических полей и уяснить такие понятия, как поток и циркуляция вектора напряженности поля. При изучении электрического поля в диэлектриках следует представлять механизм поляризации полярных и неполярных диэлектриков и преимущество вектора электрического смещения перед вектором напряженности для описания электрического поля в неоднородных диэлектриках. При изучении вопроса об энергии заряженных проводников и конденсаторов студент должен обратить внимание, что в рамках электростатики нельзя однозначно решить вопрос о локализации этой энергии. С равным правом можно считать, что энергией обладают как заряженные проводники, так и создаваемое ими электрическое поле. Изучение темы «Постоянный электрический ток» следует начать с классической электронной теории проводимости металлов, на ее основе рассмотреть законы Ома и Джоуля-Ленца. Четко разграничить такие понятия, как разность потенциалов, электродвижущая сила и электрическое напряжение. Изучая раздел «Магнитное поле», студент должен уделить особое внимание закону Ампера, знать и уметь применять закон Био-Савара-Лапласа для расчета магнитной индукции или напряженности магнитного поля прямолинейного и кругового токов, а также закон полного тока (циркуляция вектора магнитной индукции) для расчета магнитного поля тороида и длинного соленоида. При изучении вопроса, связанного с действием магнитного поля на движущиеся заряды, нужно уметь применять силу Лоренца для определения направления движения заряженных частиц в магнитном поле, представлять себе принцип действия циклических ускорителей заряженных частиц, а также определять работу перемещения проводника и контура с током в магнитном поле. При изучении явления электромагнитной индукции необходимо усвоить, что механизм возникновения ЭДС индукции имеет электронный характер. Изучив основной закон электромагнитной индукции Фарадея-Максвелла, студент на его основе должен уметь вывести и применять для расчетов формулы электродвижущей силы индукции, энергии магнитного поля. Изучение магнитных свойств вещества носит, в основном, описательный характер. Студент при этом должен уяснить, что исходя из выражения циркуляции вектора магнитной индукции, магнитное поле, в отличие от электрического, является вихревым. Студенту следует ясно представлять себе физический смысл уравнений Максвелла (в интегральной форме), знать, что переменные электрическое и магнитное поля взаимосвязаны, они поддерживают друг друга и могут существовать независимо. Под энергией электромагнитного поля следует подразумевать сумму энергий электрического и магнитного полей. Контрольная работа № 2 представлена набором таких задач, которые помогут студенту проверить свои знания по разделам «Электростатика», «Постоянный ток», «Электромагнетизм». Она включает в себя задачи на определение напряженности и разности потенциалов электрического поля, расчет простейших электрических полей с помощью принципа суперпозиции, определение электроемкости и энергии поля конденсаторов, применение законов Ома и Джоуля-Ленца. Включены задачи на применение закона Био-Савара-Лапласа для расчета магнитной индукции (или напряженности) магнитного поля, создаваемого проводниками с током различной конфигурации, применение принципа суперпозиции при определении индукции или напряженности простейших полей, определение траектории движения заряженной частицы, ее удельного заряда и силы, действующей на движущуюся частицу в магнитном поле, вычисление работы, совершаемой силами как при движении прямолинейного проводника с током, так и при вращении контура с током различной конфигурации в магнитном поле, нахождение намагниченности, энергии и объемной плотности энергии магнитного поля соленоида и тороида. ОСНОВНЫЕ ФОРМУЛЫ ЭЛЕКТРИЧЕСТВО Закон Кулона: где q1 и q2 – величины точечных зарядов, Напряженность электрического поля: Напряженность поля: точечного заряда: бесконечно длинной заряженной нити: равномерно заряженной бесконечной плоскости: между двумя разноименно заряженными, бесконечными плоскостями:
где Работа по перемещению заряда в электростатическом поле: где Потенциал поля точечного заряда: Связь между потенциалом и напряженностью: Сила притяжения между двумя разноименно заряженными обкладками конденсатора: где S – площадь пластин. Электроемкость уединенного проводника: плоского конденсатора: слоистого конденсатора: где d – расстояние между пластинами конденсатора, di – толщина i-го слоя диэлектрика, Электроемкость батареи конденсаторов, соединенных: параллельно: последовательно: Энергия поля: заряженного проводника: заряженного конденсатора: где V – объем конденсатора. Объемная плотность энергии электрического поля: Сила тока: Закон Ома для участка цепи в дифференциальной форме: в интегральной: где Закон Джоуля-Ленца в дифференциальной форме: в интегральной форме: Сопротивление однородного проводника: где Зависимость удельного сопротивления от температуры: где МАГНЕТИЗМ Сила Лоренца: где Сила Ампера: где I – сила тока в проводнике, dl – элемент длины проводника. Магнитный момент контура с током: где S – площадь контура. Механический момент, действующий на контур с током в магнитном поле: Закон Био-Савара-Лапласа: где Магнитная индукция: в центре кругового тока: поля бесконечного длинного прямого тока: поля, созданного отрезком проводника с током:
поля бесконечно длинного соленоида: где R – радиус кругового тока, r – кратчайшее расстояние до оси проводника, n – число витков на единицу соленоида, a1 и a2 – углы между отрезком проводника и линией, соединяющей концы отрезка с точкой поля. Сила взаимодействия двух прямолинейных бесконечно длинных параллельных токов на единицу их длины: где r – расстояние между проводниками с токами I1и I2. Работа по перемещению контура с током в магнитном поле: где Ф – магнитный поток через поверхность контура. Магнитный поток однородного магнитного поля через площадку S:
где a – угол между вектором Закон электромагнитной индукции: где N – число витков контура. Потокосцепление контура с током: где L – индуктивность контура. Электродвижущая сила самоиндукции: Индуктивность соленоида: где V – объем соленоида, n – число витков на единицу длины соленоида. Мгновенное значение сила тока в цепи, обладающей сопротивлением R и индуктивностью L: Энергия магнитного поля: Объемная плотность энергии магнитного поля:
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1. В углах при основании равнобедренного треугольника с боковой стороной 8 см расположены заряды Q1 и Q2. Определить силу, действующую на заряд Q2 равный 1нКл, помещенный в третью вершину треугольника, угол при которой 120°. Рассмотреть случаи: а) Q1= Q2 = 2 нКл; б) ½Q1½=½-Q2 ½= 2 нКл. Решение. В соответствии с принципом суперпозиции поле каждого из зарядов Q1 и Q2 действует на заряд Q3 независимо. Это значит, что на заряд Q3 действуют силы (рис. 1, а): В случае разноименных зарядов Q1 и Q2 из рис.1,б видно, что угол b = 60° и, следовательно, F2=4,8×10-6 Н.
2. Два равных отрицательных заряда по 9 нКл находятся в воде на расстоянии l=8 см друг от друга. Определить напряженность и потенциал поля в точке, расположенной на расстоянии h=5 см от линии, соединяющей заряды. Решение. Напряженность поля, создаваемого в точке А (рис.2) зарядами Q1 и Q2 по принципу суперпозиции полей, равна векторной сумме напряженностей, создаваемых каждым из зарядов:
Напряженность поля точечного заряда Q: Ответ: Е = 480 В/м; 3. Заряд 1 нКл переносится в воздухе из точки, находящейся на расстоянии 1 м от бесконечно длиной равномерно заряженной нити, в точку на расстоянии 10 см от нее. Определить работу, совершаемую против сил поля, если линейная плотность заряда нити 1 мкКл/м. Какая работа совершается на последних 10 см пути? Решение. Работа внешней силы по перемещению заряда Q из точки поля с потенциалом Бесконечная равномерно заряженная нить с линейной плотностью заряда t создает аксиально-симметричное поле напряженностью Подставляя в формулу (1) найденное выражение для разности потенциалов из (2), определим работу, совершаемую внешними силами по перемещению заряда из точки, находящейся на расстоянии 1 м, до точки, расположенной на расстоянии 0,1 м от нити: Ответ: А1 = 4,1×10-5 Дж; А2 = 1,25×10-5Дж. 4. К одной из обкладок плоского конденсатора прилегает стеклянная плоскопараллельная пластинка (e=7) толщиной 9 мм. После того как конденсатор отключили от источника напряжения 220 В и вынули стеклянную пластинку, между обкладками установилась разность потенциалов 976 В. Определить зазор между обкладками и отношение конечной и начальной энергии конденсатора. Решение. После отключения конденсатора и удаления стеклянной пластинки заряд на его обкладках остается неизменным, т.е. выполняется равенство: где С1 и С2 – электроемкости конденсатора в начальном и конечном случае. По условию конденсатор вначале является слоистым и его электроемкость определяется по формуле: где S – площадь обкладок; d0 – зазор между ними, d1 – толщина стеклянной пластинки; ε1 и ε2 – диэлектрические проницаемости стекла и воздуха соответственно. После удаления стеклянной пластинки электроемкость конденсатора: Подставляя (2) и (3) в (1), получим:
Ответ: d0 = 10-2 м; W2/W1 = 4,44. 5. Батарею из двух конденсаторов емкостью 400 и 500 пФ соединили последовательно и включили в сеть с напряжением 220 В. Потом батарею отключили от сети, конденсаторы разъединили и соединили параллельно обкладками, имеющими одноименные заряды. Каким будет напряжение на зажимах полученной батареи? Решение. У последовательно соединенных конденсаторов заряды на обкладках равны по модулю Q1 = Q2 = Q и заряд батареи равен заряду одного конденсатора. Емкость батареи последовательно соединенных конденсаторов определяется по формуле: При отключении конденсаторов их заряд сохраняется. У параллельно соединенных конденсаторов заряд батареи равен сумме зарядов конденсаторов Q' = Q1 + Q2, а емкость сумме емкостей: Подставляя (1) в (2), получаем: Ответ: 6. Заряд конденсатора 1 мкКл, площадь пластин 100 см2, зазор между пластинками заполнен слюдой. Определить объемную плотность энергии поля конденсатора и силу притяжения пластин. Решение. Сила притяжения между двумя разноименно заряженными обкладками конденсатора: где Е – напряженность поля конденсатора; S – площадь обкладок конденсатора; ε – диэлектрическая проницаемость слюды; ε0 – электрическая постоянная. Напряженность однородного поля плоского конденсатора: где Подставляя (2) в (3), получаем: Ответ: 7. В медном проводнике сечением 6 мм и длиной 5 м течет ток. За 1 мин в проводнике выделяется 18 Дж теплоты. Определить напряженность поля, плотность и силу электрического тока в проводнике. Решение. Для решения задачи используем законы Ома и Джоуля-Ленца. Закон Ома в дифференциальной форме имеет вид: где j – плотность тока; Е – напряженность поля; γ – удельная проводимость. Закон Джоуля-Ленца: здесь I – сила тока, t – время. Ответ: 8. Внутреннее сопротивление аккумулятора 2 Ом. При замыкании его одним резистором сила тока равна 4 А, при замыкании другим – 2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить электродвижущую силу аккумулятора и внешние сопротивления. Решение. Закон Ома для замкнутой (полной) цепи имеет вид:
где r – внутреннее сопротивление источника тока; ξ – э.д.с. аккумулятора; R1 и R2 – внешние сопротивления цепей. Уравнения (1) представим в виде:
Из равенства (2) следует, что:
Мощность, выделяемая во внешней цепи в первом и втором случаях, cоответственно равна:
Решая совместно уравнения (3) и (4), получаем:
Подставляя (5) в (2), получаем: Ответ: 9. Электродвижущая сила батареи равна 20 В. Коэффициент полезного действия батареи составляет 0,8 при силе тока 4 А. Чему равно внутреннее сопротивление батареи? Решение. Коэффициент полезного действия источника тока η равен отношению падения напряжения во внешней цепи к его электродвижущей силе: Ответ: 10. По двум бесконечно длинным прямолинейным проводникам, находящимся на расстоянии 50 см друг от друга, в одном направлении текут токи Решение. В соответствии с принципом суперпозиции индукция результирующего магнитного поля в точке А равна: Ответ: 11. Электрон, пройдя ускоряющую разность потенциалов 88 кВ, влетает в однородное магнитное поле перпендикулярно его линиям индукции. Индукция поля равна 0,01 Тл. Определить радиус траектории электрона. Решение. В магнитном поле на электрон, движущийся со скоростью Ответ:
Решение. Поле внутри соленоида можно считать однородным. В этом случае напряженность поля: Ответ: В =1,7 Тл, Тл. 13. На соленоид (см. условие и решение задачи 12) надето изолированное кольцо того же диаметра. Определить электродвижущую силу индукции в кольце и электродвижущую силу самоиндукции в соленоиде, если за 0,01 с ток в его обмотке равномерно снижается до нуля. Решение. По условию за время ∆t = 0,01 с сила тока в обмотке соленоида равномерно уменьшается от 0,1 А до нуля, поэтому магнитный поток, пронизывающий площадь кольца Ответ: 14. Виток радиусом 5 см с током 1 А помещен в однородное магнитное поле напряженностью 5000 А/м так, что нормаль к витку составляет угол 60° с направлением поля. Какую работу совершат силы поля при повороте витка в устойчивое положение? Решение. Работа А при повороте витка с током Ответ:
КОНТРОЛЬНАЯ РАБОТА № 2
201. В вершинах квадрата со стороной 0,1 м расположены равные одноименные заряды. Потенциал создаваемого ими поля в центре квадрата равен 500 В. Определить заряд. 202. В вершинах квадрата со стороной 0,5 м расположены заряды одинаковой величины. В случае, когда два соседних заряда положительные, а два других – отрицательные, напряженность поля в центре квадрата равна 144 В/м. Определить величину зарядов. 203. В вершинах квадрата со стороной 0,1 м помещены заряды по 0,1 нКл. Определить напряженность и потенциал поля в центре квадрата, если один из зарядов отличается по знаку от остальных. 204. Пространство между двумя параллельными бесконечными плоскостями с поверхностной плотностью зарядов +5∙10-8 и -9∙10-8 Кл/м2 заполнено стеклом. Определить напряженность поля: а) между плоскостями; б) вне плоскостей. 205. На расстоянии 8 см друг от друга в воздухе находятся два заряда по 1 нКл. Определить напряженность и потенциал поля в точке, находящейся на расстоянии 5 см от зарядов. 206. Две параллельные плоскости одноименно заряжены и имеют поверхностную плотность зарядов 2 и 4 нКл/м2. Определить напряженность поля: а) между плоскостями; б) вне плоскостей. 207. Если в центр квадрата, в вершинах которого находятся заряды по +2 нКл, поместить отрицательный заряд, то результирующая сила, действующая на каждый заряд, будет равна нулю. Вычислить числовое значение отрицательного заряда. 208. Заряды по 1 нКл помещены в вершинах равностороннего треугольника со стороной 0,2 м. Равнодействующая сил, действующих на четвертый заряд, помещенный на середине одной из сторон треугольника, равна 0,6 мкН. Определить этот заряд, напряженность и потенциал поля в точке его расположения. 209. Два шарика массой по 0,2 г подвешены в общей точке на нитях длиной 0,5 м. Шарикам сообщили заряд и нити разошлись на угол 90°. Определить напряженность и потенциал поля в точке подвеса шарика. 210. Два одинаковых заряда находятся в воздухе на расстоянии 0,1 м друг от друга. Напряженность поля в точке, удаленной на расстоянии 0,06 м от одного и 0,08 м от другого заряда, равна 10 кВ/м. Определить потенциал поля в этой точке и значение зарядов. 211. Пылинка массой 8∙10-15 кг удерживается в равновесии между горизонтально расположенными обкладками плоского конденсатора. Разность потенциалов между обкладками 490 В, а зазор между ними 1 см. Определить, во сколько раз заряд пылинки больше элементарного заряда. 212. В поле бесконечной равномерно заряженной плоскости с поверхностной плотностью заряда 10 мкКл/м2 перемещается заряд из точки, находящейся на расстоянии 0,1 м от плоскости, в точку на расстоянии 0,5 м от нее. Определить заряд, если при этом совершается работа 1 мДж. 213. Какую работу нужно совершить, чтобы заряды 1 и 2 нКл, находившиеся на расстоянии 0,5 м, сблизились до 0,1 м? 214. Поверхностная плотность заряда бесконечной равномерно заряженной плоскости равна 30 нКл/м2. Определить поток вектора напряженности через поверхность сферы диаметром 15 см, рассекаемой этой плоскостью пополам. |
|
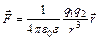 ,
, – электрическая постоянная,
– электрическая постоянная,  – диэлектрическая проницаемость среды,
– диэлектрическая проницаемость среды,  – расстояние между зарядами.
– расстояние между зарядами. .
. ,
, ,
, ,
,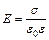 ,
, – линейная плотность заряда,
– линейная плотность заряда,  – поверхностная плотность заряда,
– поверхностная плотность заряда, 
 и
и  – потенциалы начальной и конечной точек.
– потенциалы начальной и конечной точек.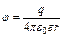 .
. .
. ,
,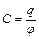 ,
, ,
,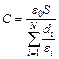 ,
,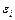 его диэлектрическая проницаемость.
его диэлектрическая проницаемость. ,
, .
.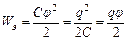 ,
,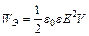 ,
, .
. .
.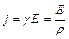 ,
,
 – удельная проводимость, r – удельное сопротивление,
– удельная проводимость, r – удельное сопротивление,  – напряжение на концах цепи,
– напряжение на концах цепи,  – сопротивление цепи,
– сопротивление цепи,  – плотность тока.
– плотность тока. ,
,

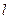 – длина проводника,
– длина проводника,  – площадь его поперечного сечения.
– площадь его поперечного сечения.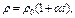
 – температурный коэффициент сопротивления,
– температурный коэффициент сопротивления,  – температура по шкале Цельсия.
– температура по шкале Цельсия. ,
,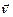 – скорость заряда,
– скорость заряда, 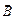 – индукция магнитного поля.
– индукция магнитного поля. ,
,
 .
. ,
, – магнитная постоянная,
– магнитная постоянная, 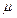 – магнитная проницаемость среды.
– магнитная проницаемость среды.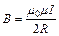 ,
, ,
,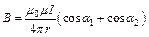 ,
, ,
, ,
, ,
, ,
, ,
,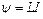 ,
, .
. .
.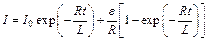 .
. .
. .
.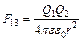 ,
,  . Так как
. Так как  , то
, то  . Векторная сумма
. Векторная сумма  является искомой величиной. Модуль силы определяется по теореме косинусов
является искомой величиной. Модуль силы определяется по теореме косинусов  В случае одноименных зарядов Q1 и Q2 из рис.1, а видно, что угол b = 120°, поэтому F1 = F13 = F23:
В случае одноименных зарядов Q1 и Q2 из рис.1, а видно, что угол b = 120°, поэтому F1 = F13 = F23: 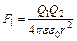 . F1=2,8×10-6 Н.
. F1=2,8×10-6 Н. ,
, Ответ: F1=2,8×10-6 Н, F2= 4,8×10-6 Н.
Ответ: F1=2,8×10-6 Н, F2= 4,8×10-6 Н. . (1)
. (1)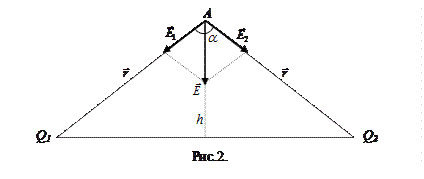 По теореме косинусов:
По теореме косинусов: 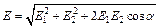 . (2)
. (2)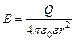 , где
, где  и
и  направлены к зарядам. По условию заряды Q1 = Q2 расположены на одинаковом расстоянии от точки А, поэтому Е1 = Е2. Следовательно, формула (2) принимает вид Е = 2Е1×cos
направлены к зарядам. По условию заряды Q1 = Q2 расположены на одинаковом расстоянии от точки А, поэтому Е1 = Е2. Следовательно, формула (2) принимает вид Е = 2Е1×cos  , где cos
, где cos  . Тогда напряженность в точке А:
. Тогда напряженность в точке А:  , E = 480 В/м. Потенциал
, E = 480 В/м. Потенциал 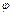 , создаваемый системой точечных зарядов в данной точке поля, равен алгебраической сумме потенциалов полей, создаваемых этими зарядами:
, создаваемый системой точечных зарядов в данной точке поля, равен алгебраической сумме потенциалов полей, создаваемых этими зарядами: 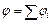 . Потенциал
. Потенциал  результирующего поля в точке А равен:
результирующего поля в точке А равен:  . Потенциал поля, создаваемого точечным зарядом,
. Потенциал поля, создаваемого точечным зарядом,  . Следовательно,
. Следовательно,  в точку с потенциалом
в точку с потенциалом  равна:
равна:  . (1)
. (1)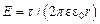 . Напряженность и потенциал этого поля связаны соотношением
. Напряженность и потенциал этого поля связаны соотношением  откуда
откуда 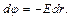 Разность потенциалов точек поля на расстоянии
Разность потенциалов точек поля на расстоянии  от нити:
от нити:  (2)
(2) , A1 = 4,1×10-5 Дж. Работа по перемещению заряда на последних 10 см пути равна:
, A1 = 4,1×10-5 Дж. Работа по перемещению заряда на последних 10 см пути равна:  , A2 = 1,25×10-5 Дж.
, A2 = 1,25×10-5 Дж. . (1)
. (1) , (2)
, (2) . (3)
. (3)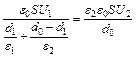 , откуда
, откуда  ,
,  м. Начальная и конечная энергии конденсатора:
м. Начальная и конечная энергии конденсатора:  ,
,  . Тогда отношение этих энергий:
. Тогда отношение этих энергий: 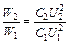 . Учитывая (1), получим:
. Учитывая (1), получим:  .
. , а их заряд:
, а их заряд:  . (1)
. (1)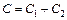 . Напряжение на зажимах батареи из двух параллельно соединенных конденсаторов:
. Напряжение на зажимах батареи из двух параллельно соединенных конденсаторов: 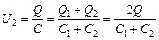 . (2)
. (2)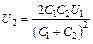 ,
,  В.
В.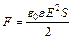 , (1)
, (1) , (2)
, (2) – поверхностная плотность заряда. Подставляя (2) в (1), получаем:
– поверхностная плотность заряда. Подставляя (2) в (1), получаем: 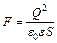 ,
,  Н. Объемная плотность энергии электрического поля:
Н. Объемная плотность энергии электрического поля: 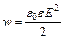 . (3)
. (3) ,
,  Дж/м3.
Дж/м3. , (1)
, (1)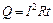 , (2)
, (2) – сопротивление проводника, где r, l, S – удельное сопротивление, длина и площадь поперечного сечения проводника соответственно. Силу тока находим из (2):
– сопротивление проводника, где r, l, S – удельное сопротивление, длина и площадь поперечного сечения проводника соответственно. Силу тока находим из (2): 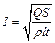 ,
,  А. По определению, плотность тока равна:
А. По определению, плотность тока равна:  ,
,  А/м2. Напряженность поля в проводнике определим из (1), учитывая, что
А/м2. Напряженность поля в проводнике определим из (1), учитывая, что  .
.  ,
, 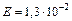 В/м.
В/м. ,
,  , (1)
, (1)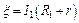 ,
,  . (2)
. (2) . (3)
. (3)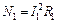 и
и  . Из условия равенства мощностей следует, что:
. Из условия равенства мощностей следует, что: . (4)
. (4) и
и  . (5)
. (5) ,
,  В,
В,  Ом,
Ом,  Ом.
Ом.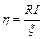 , откуда
, откуда  . Используя выражение закона Ома для замкнутой цепи
. Используя выражение закона Ома для замкнутой цепи  , получаем
, получаем  . Тогда
. Тогда  и
и 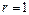 Ом.
Ом. и
и  силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током
силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током 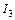 силой 5 А. Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника.
силой 5 А. Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника. , где
, где  и
и  – индукции полей, создаваемых соответственно токами
– индукции полей, создаваемых соответственно токами  – индукция поля, создаваемая кольцевым током. Векторы
– индукция поля, создаваемая кольцевым током. Векторы  равна по модулю:
равна по модулю:  . Индукция поля, создаваемого бесконечно длинным проводником с током:
. Индукция поля, создаваемого бесконечно длинным проводником с током: 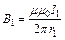 и
и  . Тогда
. Тогда 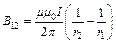 . Индукция поля, создаваемого кольцевым проводником с током:
. Индукция поля, создаваемого кольцевым проводником с током:  , где r3 – радиус кольца. Векторы
, где r3 – радиус кольца. Векторы  и
и 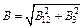 или
или  ,
,  мкТл. Напряженность магнитного поля:
мкТл. Напряженность магнитного поля:  и
и  А/м.
А/м. перпендикулярно
перпендикулярно  , которая обусловливает центростремительное ускорение электрона при его движении по окружности:
, которая обусловливает центростремительное ускорение электрона при его движении по окружности: 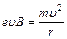 , где m – масса электрона; е – его заряд; r – радиус траектории его движения. Пройдя ускоряющую разность потенциалов U, электрон приобретает кинетическую энергию, равную работе А сил электрического поля:
, где m – масса электрона; е – его заряд; r – радиус траектории его движения. Пройдя ускоряющую разность потенциалов U, электрон приобретает кинетическую энергию, равную работе А сил электрического поля:  . Отсюда находим скорость электрона:
. Отсюда находим скорость электрона:  . Зная ее, найдем радиус траектории:
. Зная ее, найдем радиус траектории:  и
и  м.
м. 12. Соленоид длиной 20 см и диаметром 4 см имеет плотную трехслойную обмотку из провода диаметром 0,1 мм. По обмотке соленоида течет ток 0,1 А. Зависимость B = f(H) для материала сердечника приведена на рис. 3. Определить напряженность и индукцию поля в соленоиде, магнитную проницаемость сердечника, индуктивность соленоида, энергию и объемную плотность энергии поля соленоида.
12. Соленоид длиной 20 см и диаметром 4 см имеет плотную трехслойную обмотку из провода диаметром 0,1 мм. По обмотке соленоида течет ток 0,1 А. Зависимость B = f(H) для материала сердечника приведена на рис. 3. Определить напряженность и индукцию поля в соленоиде, магнитную проницаемость сердечника, индуктивность соленоида, энергию и объемную плотность энергии поля соленоида.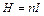 , где
, где  – сила тока в обмотке;
– сила тока в обмотке;  число витков, приходящихся на единицу длины соленоида. Тогда:
число витков, приходящихся на единицу длины соленоида. Тогда:  и
и  300А/м. По графику В = f(H) находим, что напряженности 3000 А/м соответствует индукция 1,7 Тл. Используя связь между индукцией и напряженностью:
300А/м. По графику В = f(H) находим, что напряженности 3000 А/м соответствует индукция 1,7 Тл. Используя связь между индукцией и напряженностью:  , определим магнитную проницаемость:
, определим магнитную проницаемость: 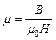 и
и  . Индуктивность соленоида:
. Индуктивность соленоида:  , где l – длина,
, где l – длина,  – площадь поперечного сечения соленоида. Получаем:
– площадь поперечного сечения соленоида. Получаем:  . Объемная плотность энергии магнитного поля:
. Объемная плотность энергии магнитного поля:  и
и 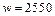 Дж/м3. Энергия магнитного поля соленоида:
Дж/м3. Энергия магнитного поля соленоида:  и
и 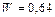 Дж.
Дж. до
до  . Электродвижущая сила индукции, возникающая в кольце:
. Электродвижущая сила индукции, возникающая в кольце:  и
и  B. Электродвижущая сила самоиндукции ξS , возникающая в соленоиде при выключении тока в нем:
B. Электродвижущая сила самоиндукции ξS , возникающая в соленоиде при выключении тока в нем: 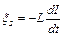 . Так как при выключении сила тока уменьшается до нуля равномерно, то:
. Так как при выключении сила тока уменьшается до нуля равномерно, то:  . Тогда:
. Тогда:  и
и  В.
В.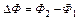 – изменение магнитного потока сквозь площадь витка
– изменение магнитного потока сквозь площадь витка  ;
; 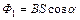 – магнитный поток, пронизывающий виток в начальном положении, где α – угол между векторами
– магнитный поток, пронизывающий виток в начальном положении, где α – угол между векторами  и
и  . Следовательно,
. Следовательно,  . Таким образом,
. Таким образом,  . Учитывая, что
. Учитывая, что  . Окончательно имеем:
. Окончательно имеем:  и
и  Дж.
Дж.