|
|
Адсорбция на поверхности твердых тел.Твердые тела обладают способностью адсорбировать из окружающей среды на своей поверхности молекулы, атомы или ионы. Процессы адсорбции на твердой поверхности аналогичны процессам адсорбции на жидкой поверхности, т.е. на поверхности твердого адсорбента адсорбируются твердые вещества, понижающие поверхностное натяжение его относительно окружающей среды. Очевидно, что при прочих равных условиях для данных адсорбента и адсорбата, адсорбция будет тем больше, чем больше поверхность адсорбента. Поэтому хорошими адсорбентами могут быть материалы, обладающие сильно развитой поверхностью, имеющие сильно пористую, губчатую структуру, или материалы, находящиеся в состоянии тонкого измельчения. Из применяемых в практике адсорбентов первое место принадлежит различным видам специально изготовленных адсорбционных углей (древесный, кровяной, костный и др.). Они могут обладать исключительно развитой поверхностью пор. Так, 1 г активированного угля обладает внутренней поверхностью пор, достигающей 400-900 м2. Кроме активных (активированных) углей в качестве адсорбентов применяются такие вещества как селикогель, кремнезем, каолин и др. Явление капиллярной конденсации Твердый адсорбент может содержать поры в виде узких каналов диаметром порядка 10-7 см, т.е. капилляры. В таких капиллярах кроме обычной адсорбции, может происходить капиллярная конденсация паров. Если жидкость хорошо смачивает стенки капилляра, то мениск ее всегда бывает выгнутым. В этих условиях давление насыщенного пара будет более низким, чем над плоской поверхностью, насыщение паров и их конденсация будет происходить раньше чем достигается состояние насыщения (точка росы) для большой плоской поверхности. Пары будут конденсироваться в жидкость в капиллярах. Такое явление получило название капиллярной конденсации. Многие родные и искусственные материалы (почвы, рыхлые известняки, уголь и др.) обладают сильно развитой системой капилляр и пор. В них способны конденсироваться пары воды или других жидкостей, не являющихся насыщенными к обычной плоской поверхности. Адсорбция из растворов Изотермы адсорбции растворенных веществ из растворов аналогичны изотермам адсорбции газов (изотерма Ленгмюра), но адсорбция из растворов, являющихся многокомпонентными системами, осложняется одновременной адсорбцией растворенного вещества и растворителя. (уравнение адсорбции Гиббса ds=-SdmiГi) Рассмотрим адсорбцию вещества из бинарных растворов (растворитель – В, растворенное вещество – А).
Для состояния адсорбционного равновесия можно записать такое уравнение: А+(В)«(А)+В, где А и (А) – молекулы растворенного вещества в объеме раствора и на адсорбенте; В и (В) – молекулы растворителя в объеме раствора и на адсорбенте. Как для всякой химической реакции константа равновесия (К) определяется выражением:
Если концентрацию А и В выразить в мольных долях, то есть общее число молей в растворе N=A+B, и общее число молей на адсорбенте (N)=(A)+(B), тогда А/N+В/N=1 или NA+NB=1, и (NA)+(NB)=1. Соответственно константа адсорбционного равновесия равна
Выражая NВ=1-NA и (NВ)=1-(NA), получим
Это выражение (1) представляет собой уравнение изотермы адсорбции из бинарного раствора. Проанализируем его: 1) если Na®0, т.е. концентрация растворенного вещества мала, то (NA)@кNA, т.е. это уравнение Генри. 2) Если Na®1, т.е. раствор состоит почти из растворенного вещества (NA®0 – растворителя почти нет), то (NA) ®1, т.е. в адсорбционном слое почти одно вещество А. 3) Если вещество А сильно адсорбируется на адсорбенте, то К>>1 и 4) Если вещество А слабо адсорбируется на адсорбенте, то К<<1 и Это выражение показывает, что мольная доля вещества А на поверхности адсорбции мала при любых Na и начинает быстро возрастать лишь при NA®1. На рассмотренном примере, адсорбция растворенного вещества А выражается величиной (NA), а график изотермы адсорбции вещества А на поверхности адсорбента (NA)=f(NA) будет выглядеть так: 1 – так выглядит зависимость (NA)=f(NA), если вещество А сильно адсорбируется на поверхности адсорбента; 2 - при слабой адсорбции вещества А на поверхности адсорбента; 3 – при средней адсорбции вещества А на поверхности адсорбента, т.е. когда адсорбция растворенного вещества А и растворителя В примерно одинаковы (следует иметь в виду, что на поверхности адсорбента при любом значении Na в растворе “свободные места” заняты молекулами растворителя на веществе А, но в различных соотношениях). В практике химиков-энергетиков явление адсорбции встречаются в химанализе (газовая, жидкостная, ионообменная хромотография), а главным образом в процессах ионного обмена, при коагуляции и обезмасливание конденсата и паров.
Анализ уравнения Ленгмюра
При адсорбции действуют в основном дисперсионные силы, которые вызываются согласованным движением электронов в сближающихся молекулах. Из-за этого даже молекулы с симметричным распределением электронной плотности испытывают колеблющиеся по направлению движения отклонения от этой плотности. При сближении молекул эти колебания теряют независимость, что и вызывает притяжение. Часто имеют значение электростатические силы: ориентационные силы при адсорбции полярных молекул на поверхностях с постоянными электростатическими зарядами и индукционные, обусловленные появлением в адсорбирующихся молекулах дипольных моментов, наведенных зарядами поверхности, или появлением дипольных моментов в адсорбенте, наведенных адсорбирующимися диполями. Перечисленные силы являются силами притяжения. При сближении молекул адсорбата и адсорбента они уравновешиваются силами отталкивания, которые быстро растут на коротких расстояниях. Адсорбирующаяся молекула взаимодействует со многими центрами на поверхности адсорбента. На практике при расчетах учитывается взаимодействие с 100–200 ближайшими атомами адсорбента. Во многих случаях энергия индукционного и ориентационного взаимодействия много больше энергии дисперсионного взаимодействия, поэтому часто принимается, что последняя определяет энергию межмолекулярного притяжения. При адсорбции часто происходит образование водородной связи, например, в случае молекул воды, спиртов, эфиров, аминов на адсорбентах, поверхность которых покрыта гидроксильными группами (силикагель ). Теория мономолекулярной адсорбции предложена Ленгмюром в 1915 году. При выводе уравнения учитывались следующие положения. 1. Адсорбция локализована и вызвана силами, близкими к химическим. 2. Адсорбция происходит на активных центрах на поверхности адсорбента (пики). Активные центры занимают незначительную часть поверхности. 3. Каждый активный центр адсорбирует только одну молекулу адсорбата, и на поверхности образуется его молекулярный слой. 4. Адсорбированные молекулы удерживаются активными центрами в течение определенного времени, которое зависит от температуры. 5. Силами взаимодействия между адсорбированными молекулами можно пренебречь. Для вывода уравнения представим локализованную адсорбцию газа как квазихимическую реакцию между молекулами газа и активным центром адсорбента с образованием адсорбционного комплекса:
молекула газа + активный центр адсорбента ® адсорбционный комплекс.
В этом случае где Поскольку каждый активный центр может занять одна молекула, то
где :
и подставим в (2.4):
Решив его относительно
Это уравнение адсорбции Ленгмюра. Его иногда записывают в виде
Поскольку a пропорционально где Уравнение Ленгмюра пригодно для описания адсорбции газов и растворенных веществ. Чтобы получить выражение, пригодное для графического решения, делят давление р на обе части уравнения:
Это уравнение прямой в координатах р/a – р (рис. 2.2). Оно хорошо описывает адсорбцию, обусловленную силами, близкими по своей природе к химическим.
Рис. 2.2. Графическое решение уравнения Ленгмюра В некоторых случаях наблюдается ступенчатая адсорбция, когда изотерма состоит из ряда ступеней. По теории Ленгмюра это обусловлено тем, что на поверхности адсорбента существуют группы активных центров с резко различной активностью.
|
|
 .
. .
. . (1)
. (1) - это уравнение подобно уравнению Ленгмюра.
- это уравнение подобно уравнению Ленгмюра.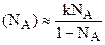
 , (2.4)
, (2.4) – поверхностная концентрация адсорбата,
– поверхностная концентрация адсорбата, 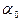 – концентрация свободных активных центров на поверхности адсорбента, P – давление газа, k – константа, не зависящая от концентрации, или давления и постоянная при данной температуре.
– концентрация свободных активных центров на поверхности адсорбента, P – давление газа, k – константа, не зависящая от концентрации, или давления и постоянная при данной температуре. , (2.5)
, (2.5) – поверхностная концентрация адсорбата при заполнении всех активных центров. Уравнение (2.5) запишем в виде
– поверхностная концентрация адсорбата при заполнении всех активных центров. Уравнение (2.5) запишем в виде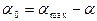 (2.6)
(2.6)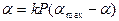 . (2.7)
. (2.7) . (2.8)
. (2.8)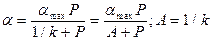 .
.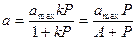 , (2.9)
, (2.9) 
 – количество адсорбата в молях, адсорбированное 1 граммом адсорбента при полном заполнении активных центров.
– количество адсорбата в молях, адсорбированное 1 граммом адсорбента при полном заполнении активных центров. . (2.10)
. (2.10)