|
|
Пример расчета плоской фермыПлоская ферма, изображенная на рисунке 4.2, находится в равновесии под действием сил F1, F2, F3. Определить реакции внешних связей и внутренние силы, действующие со стороны стержней на узлы плоской фермы. Дано: F1 = 2 кН, F2 = 6 кН, F3 = 10 кН. Решение.
 1 Определяем реакции внешних связей. 1 Определяем реакции внешних связей.
Реакция цилиндрического шарнира (точка А) включает составляющие RAx и RAy (рисунок 4.3). В точке В конструкция взаимодействует с гладкой поверхностью, реакция которой RВ перпендикулярна поверхности.
Рассматривая геометрию фермы, находим:
Замечание.При составлении уравнения моментов использована теорема Вариньона о моменте равнодействующей системы сходящихся сил (см. п. 1.1.4). Решаем полученную систему уравнений. Из уравнения (4.1) получаем
Уравнение (4.3) дает:
Из уравнения (4.2) находим:
Выполним проверку. Для этого составим уравнение моментов относительно точки С, через которую не проходят линия действия искомых реакций:
Из схемы фермы находим: Подставляем в уравнение (4.4) численные значения реакций, полученные в результате решения системы уравнений (4.1)–(4.3):
Замечание. При правильных расчетах полученное значение не должно превышать 0,5 % от наибольшего (по модулю) слагаемого уравнения. 2 Рассчитаем внутренние силы, действующие на узлы фермы, способом вырезания узлов. Обозначим узлы буквами, как это показано на рисунке 4.3. На каждый из них действуют силы реакций стержней фермы, которые пока неизвестны. Поэтому число неизвестных сил, действующих на каждый узел, в данный момент равно числу стержней, сходящихся в нем. Таким образом, наименьшее число неизвестных сил (по две) действуют на узлы В и D.
Так как
Из них получаем:
Решая их, находим:
Отсюда
Уравнение (4.4) используем с целью проверки. Для этого подставим в него численные значения величин и проверим выполнение равенства:
Подставляем найденные численные значения:
Равенство нулю последних выражений подтверждает правильность расчетов по определению внутренних сил, действующих на узлы фермы.
Рассечение фермы выполним по стержням 2-4 (рисунок 4.10).
Решаем полученную систему уравнений:
Численные значения реакций стержней, полученные при использовании методов вырезания узлов и сечений, совпали. Это подтверждает правильность полученных результатов.
4.3 Условие задания С-4 Расчет сил, действующих на плоскую ферму 1 Определить реакции внешних связей, наложенных на ферму (рисунок 4.12). Выполнить проверку. Для этого составить уравнение моментов относительно точки, через которую не проходят линии действия искомых реакций. 2 Рассчитать все внутренние силы фермы способом вырезания узлов. 3 Выполнить рассечение фермы на две части и рассчитать внутренние силы в стержнях, попавших в сечение. 12 |
|


 На ферму действует система несходящихся сил, расположенных в одной плоскости. Составляем три уравнения равновесия:
На ферму действует система несходящихся сил, расположенных в одной плоскости. Составляем три уравнения равновесия: ;
;  ; (4.1)
; (4.1) ;
;  ; (4.2)
; (4.2)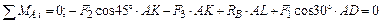 . (4.3)
. (4.3) ,
,  ,
, 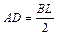 .
.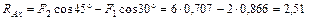 кН.
кН. кН.
кН.

 . (4.4)
. (4.4) ,
,  .
.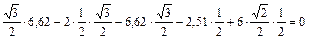 (верно).
(верно).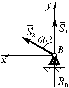 Расчет начнем с узла В (рисунок 4.4).
Расчет начнем с узла В (рисунок 4.4). ;
; .
. , то находим, что
, то находим, что  .
. 

 Теперь определим по две неизвестные силы в узлах L и D. Вырезаем узел L (рисунок 4.5). Его уравнения равновесия имеют вид:
Теперь определим по две неизвестные силы в узлах L и D. Вырезаем узел L (рисунок 4.5). Его уравнения равновесия имеют вид: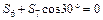 ;
; .
. Решая их, находим:
Решая их, находим: кН;
кН; кН.
кН.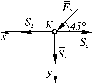 Теперь рассмотрим равновесие узла К (рисунок 4.6). Его уравнения равновесия:
Теперь рассмотрим равновесие узла К (рисунок 4.6). Его уравнения равновесия: ;
; .
.
 кН;
кН; кН.
кН. Рассмотрим равновесие узла D (рисунок 4.7). Запишем уравнения равновесия:
Рассмотрим равновесие узла D (рисунок 4.7). Запишем уравнения равновесия: ;
; .
.
 кН;
кН; кН.
кН. Для определения реакции стержня 3, рассмотрим равновесие узла А (рисунок 4.8):
Для определения реакции стержня 3, рассмотрим равновесие узла А (рисунок 4.8): ;
; . (4.5)
. (4.5)
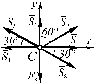
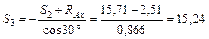 кН.
кН. (верно).
(верно). Остался нерассмотренным узел С (рисунок 4.9). Его также используем для проверки. Запишем уравнения равновесия этого узла:
Остался нерассмотренным узел С (рисунок 4.9). Его также используем для проверки. Запишем уравнения равновесия этого узла: .
. .
. (верно);
(верно); (верно).
(верно). 3 Рассчитаем внутренние силы, действующие на узлы фермы, методом сечений.
3 Рассчитаем внутренние силы, действующие на узлы фермы, методом сечений. Рассмотрим равновесие части фермы, расположенной левее сечения. При расстановке сил учитываем активные силы и силы взаимодействия частей конструкции: S2, S3, S4 (рисунок 4.11). Таким образом, на отсеченную часть действует система несходящихся сил, расположенных в одной плоскости. Запишем три уравнения равновесия:
Рассмотрим равновесие части фермы, расположенной левее сечения. При расстановке сил учитываем активные силы и силы взаимодействия частей конструкции: S2, S3, S4 (рисунок 4.11). Таким образом, на отсеченную часть действует система несходящихся сил, расположенных в одной плоскости. Запишем три уравнения равновесия:
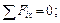




 .
.


