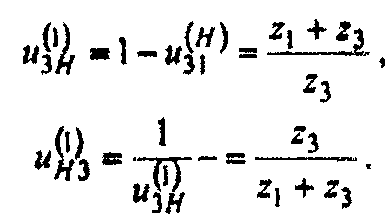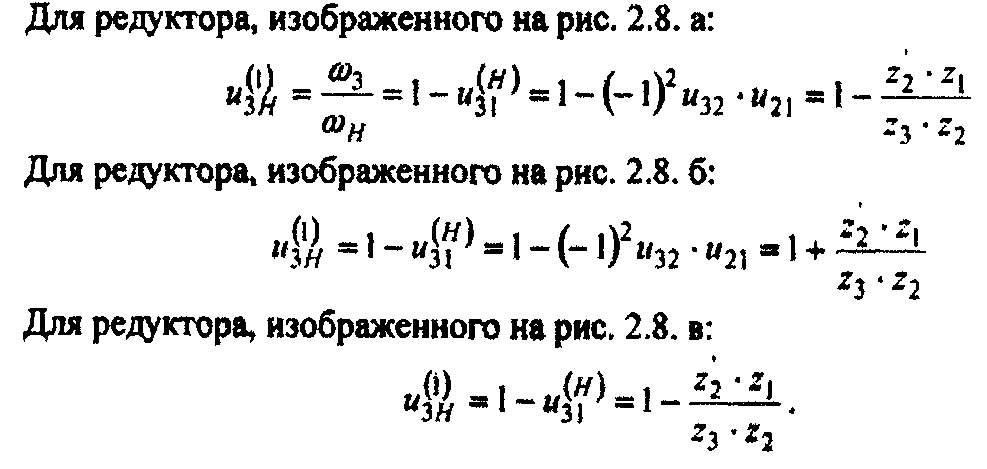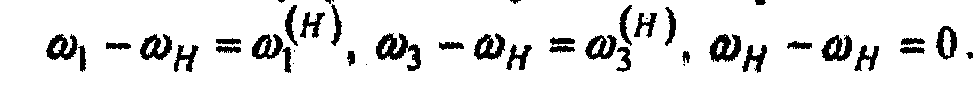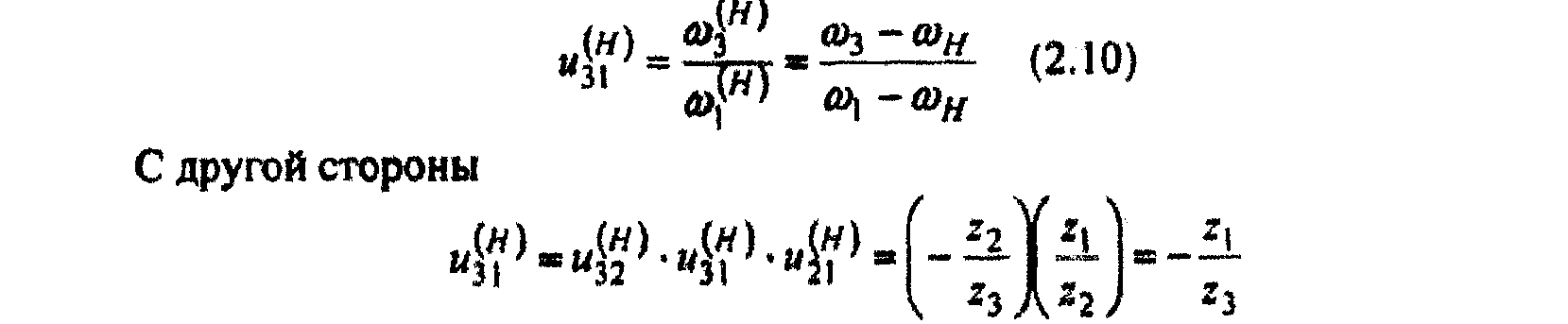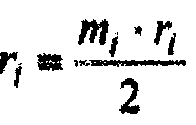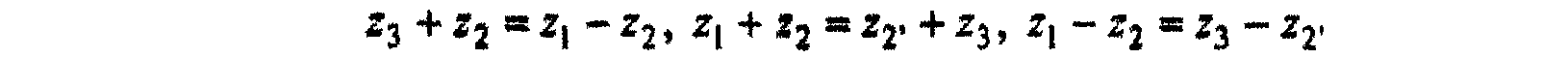|
|
Зубчатые передачи с подвижными осями.В некоторых многоступенчатых зубчатых передачах оси отдельных колес являются подвижными. Такие зубчатые механизмы с одной степенью свободы называются планетарными механизмами, а с двумя и более степенями свободы - дифференциальными механизмами или просто дифференциалами. В этих механизмах колеса с подвижными осями вращения называются планетарными колесами или сателлитами, а звено, на котором располагаются оси сателлитов - водилом. На схемах водило принято обозначать буквой H. Зубчатые колеса с неподвижными осями вращения называются солнечными или центральными, неподвижное колесо - опорным. На рис. 2.6, показан простой планетарный механизм (редуктор Джемса), в котором колесо 1 является опорным, кололо 2 - сателлитом, колесо 3 - центральным, а звено H - водилом. В рассматриваемом механизме три подвижных эвена (водило Н, колесо 2 и колесо 3) и неподвижное звено (колесо 1 жестко связано со стойкой 0). Эти звенья образуют три вращательные кинематические пары V класса (звенья 0-H, 2-Н, 3-1) и две пары IV класса (звенья 1-2 и 2-3). По структурной формуле находим число степеней свободы планетарного механизма:
Для определения передаточного отношения планетарных механизмов применяется известный метод обращения движения (метод инверсии). Сообщим механизму в целом, т.е. всем его звеньям (в том числе и стойке), вращение со скоростью ωН в обратном направлении, при этом относительное движение звеньев не изменится. В обращенном движении водило Н, вращая с собственной скоростью, ωН и вместе со всем механизмом в обратном направлении с такой же скоростью, будет оставаться как бы (мысленно) неподвижным, и механизм из планетарного превращается в механизм, состоящий из двух последовательно соединенных пар зубчатых колес 3,2 и 2,1 с неподвижными осями вращения. Для обращенного механизма передаточного отношения от колеса к колесу 1, с одной стороны, можно определить так:
C другой стороны, вычитая из угловых скоростей колес угловую скорость ωН, получим угловые скорости колес обращенного механизма, т.е. при неподвижном водиле Н.
Определяя передаточное отношение обращенного механизма, получим
из (2.7) видно, что передаточное отношение и3Н есть передаточное отношение от колеса 3 к водилу H при неподвижном колесе 1. В дальнейшем, чтобы знать, при каком неподвижном звене определено то или иное передаточное отношение, будем у передаточного отношения в скобках ставить индекс того эвена, которое принято за неподвижное. Тогда уравнение (2.7) перепишем так:
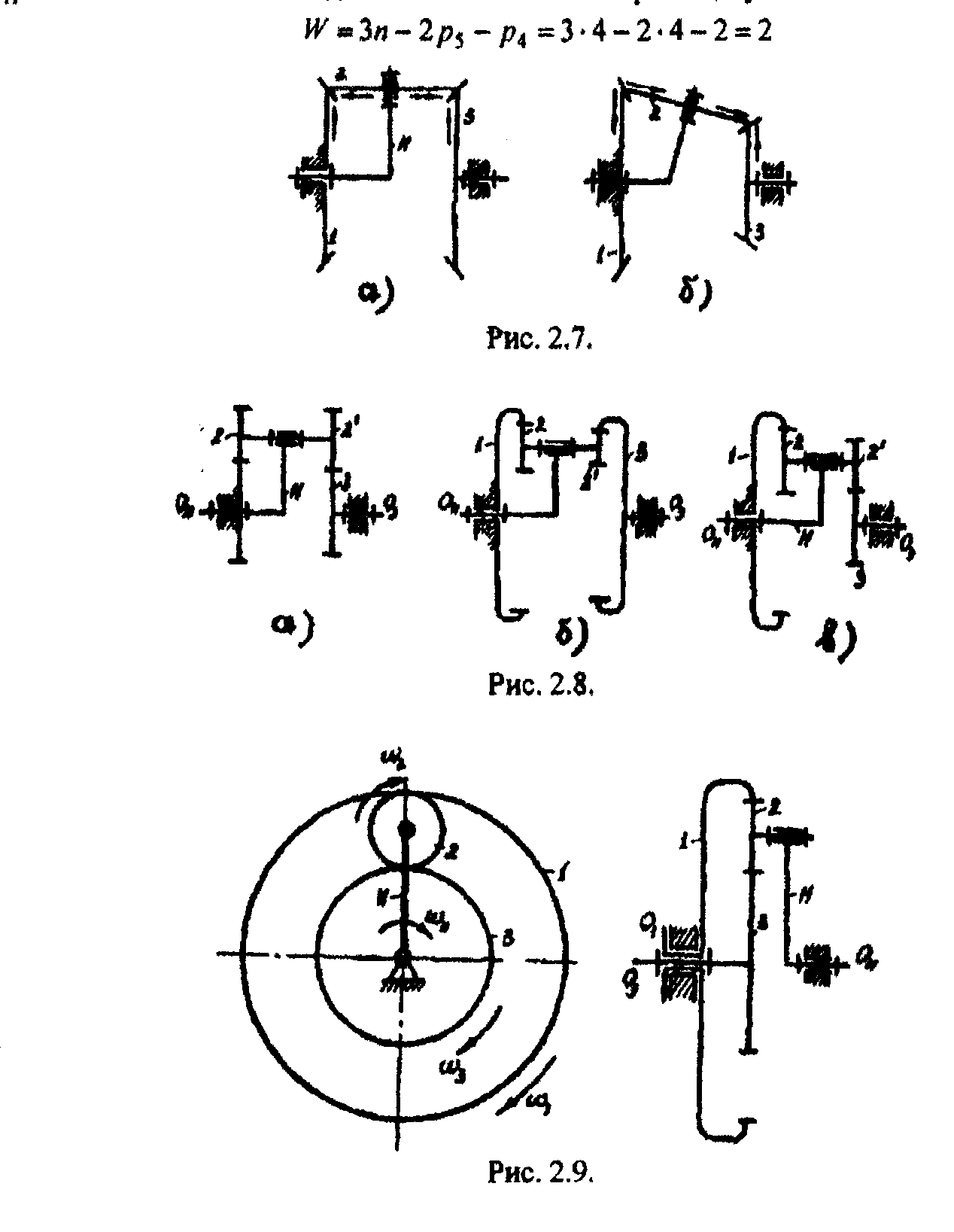
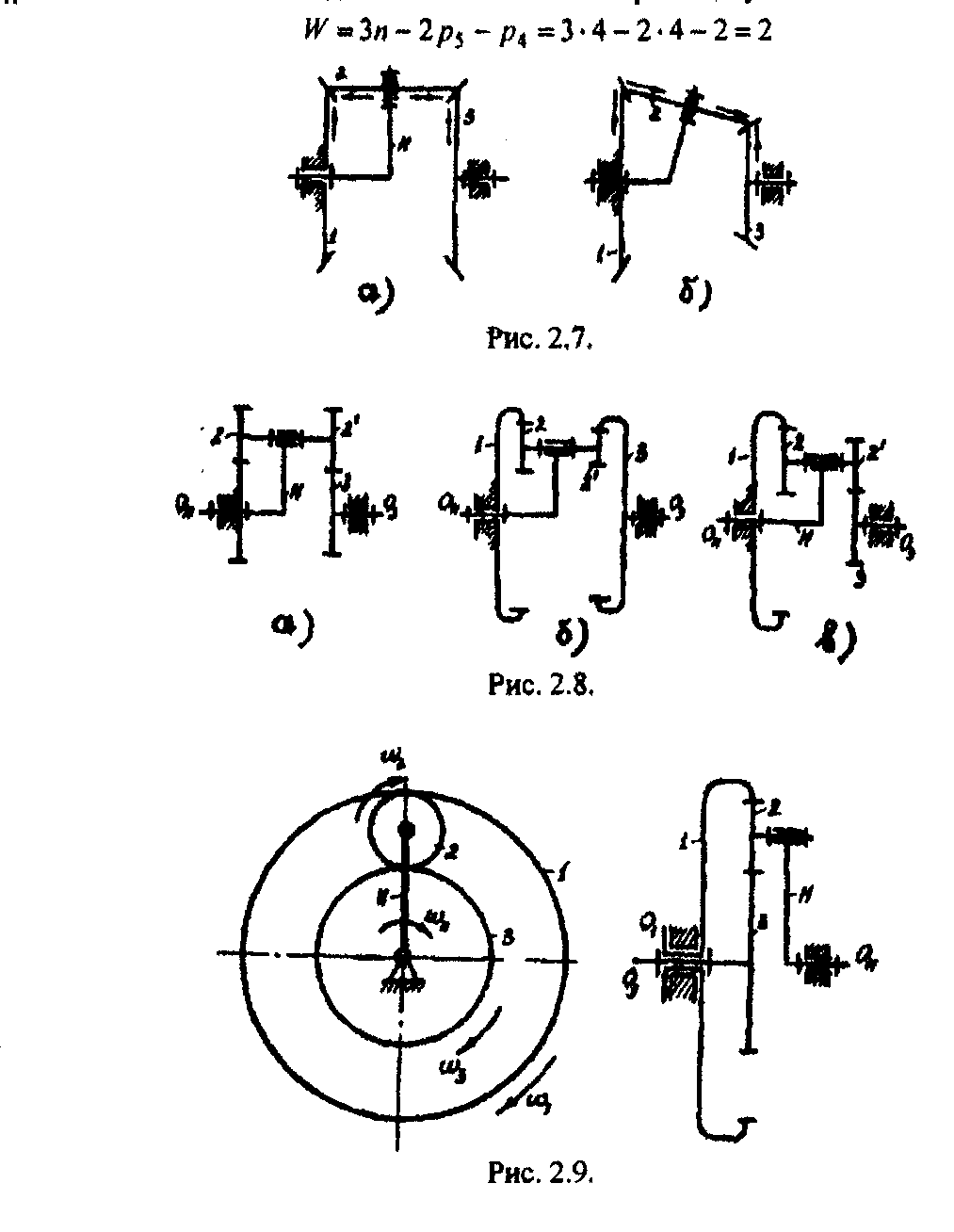
На рис. 2.7 а, б показаны схемы планетарных редукторов типа Джемса с коническими зубчатыми колесами. В соответствии с правилом (методом стрелок), указанным выше, передаточное отношение (2.5), (2.8) и (2.9).
На рис. 2,8 а, б, в показаны модификации планетарных редукторов Давида, соответственно с сателлитами, входящими в два внешних, внутренних зацепления и в смешанные зацепления. Передаточное отношение и3Н от вала O3 к валу Oh определяется по формуле (2.8).
Рассмотрим кинематику дифференциального механизма, изображенного на рис. 2.9. Колеса 1, 3 и водило H вращаются с угловыми скоростями ω1, ω3, ωН. Число степеней свободы W этого механизма равно двум
Число подвижных звеньев п = 4 (звенья 1,2, 3, Н), число кинематических пар V класса P5 = 4 (пары 1-0, 1,3 , 2-Н, Н-0), число кинематических пар IV класса P4 = 2 (пары 1-2,2-3). В этом механизме могут быть два «входа» и один выход или один вход и два «выхода»: в первом случае - зубчатый дифференциал предназначен для сложения движения входных звеньев; во втором случае - для дифференциации или разделения движения входного звена. Таким образом, определенность движения звеньев дифференциального механизма будет иметь место только в том случае, если задать движение двух звеньев. Вообще говоря, выбор этих двух звеньев может быть произвольным. Для определения угловых скоростей используем известный метод обращения движения. Пусть звенья механизма, входящие в кинематические пары со стойкой, вращаются с угловыми скоростями ω1, ω3 и ωн. Относительное движение звеньев не изменится, если всем звеньям механизма сообщить дополнительное вращение вокруг оси Oh с угловой скоростью - ωн, равной по величине, но противоположной по знаку угловой скорости ωн звена Н. Тогда звенья механизма будут иметь угловые скорости:
Следовательно, после сообщения звеньям механизма дополнительного вращения с угловой скоростью - ωн звено H будет как бы неподвижно и дифференциал превратится в обыкновенный зубчатый механизм с неподвижными осями вращения О3 и O2. Передаточное отношение такого механизма, с одной стороны, можно определить так:
Формула (2.10) (формула Виллиса) позволяет по заданным угловым скоростям двух звеньев определить угловую скорость третьего звена дифференциального механизма. В общем случае возможны три варианта: заданы угловые скорости звеньев 1 и 3, 1 и Н, 3 и Н. Рассмотренные примеры расчета передаточных отношений и угловых скоростей звеньев зубчатых редукторов предполагают заданными значения чисел зубьев всех колес. При необходимости расчета некоторых значений чисел зубьев следует использовать основное условие существования этих механизмов - условие соосности (коаксиальности). Передачи вращения, у которых оси входных и выходных валов совпадают, называются соосными передачами. Если ось вращения водила H геометрически совпадает (лежат на одной прямой) с осями вращения центральных (солнечных) колес, то такой механизм называется соосным. Математически это выражается равенством межцентровых расстояний сопряженных пар зубчатых колес. Для механизма, изображенного на рис. 2.6 и 2.9 (оси колес 1 и 3 являются соосными)
где r1, r2, r3, r4 - радиусы начальных окружностей колес 1, 2, 2', 3. Равенства (2.11), (2.12) и (2.13) называются условиями соосности. Выражая радиусы начальных окружностей через модули и числа зубьев z, получим
Когда модули зубчатых колес одинаковые (часто бывают), условия соосности, соответственно, примут вид
12 |
|
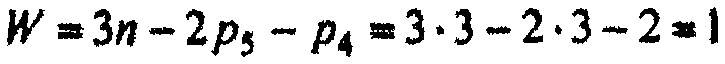
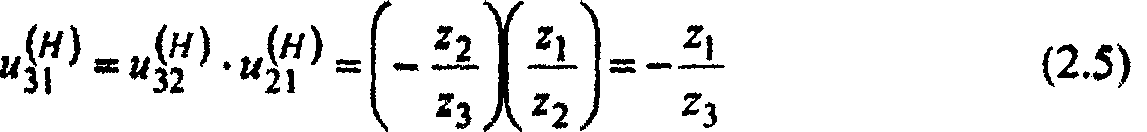
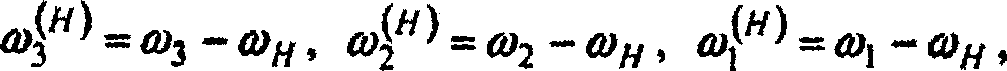
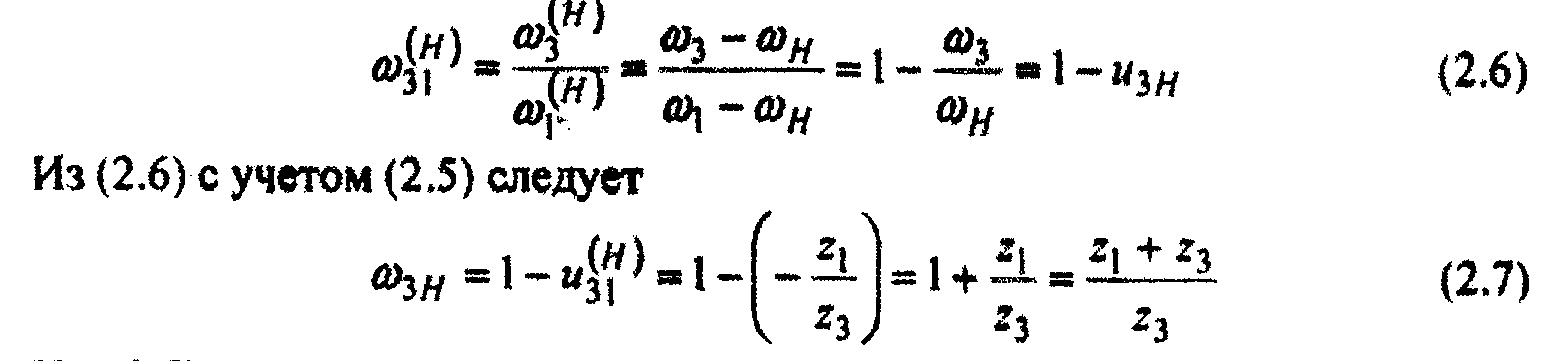
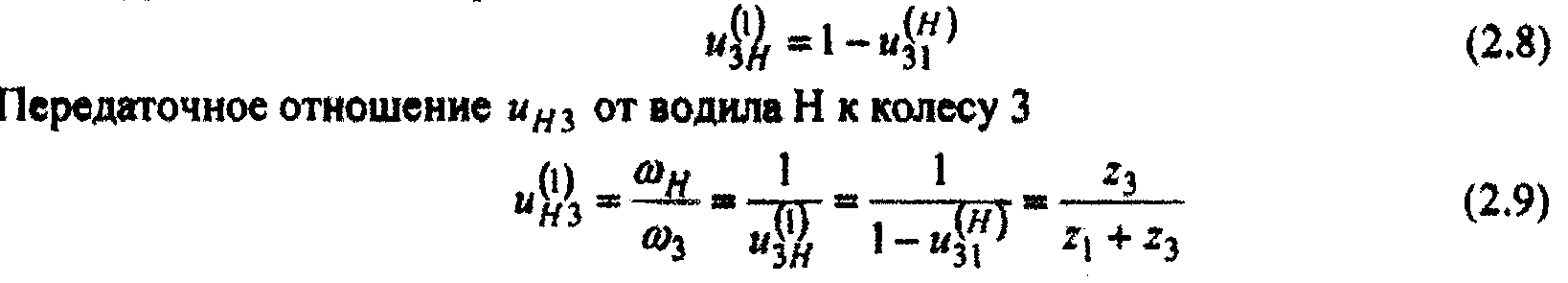
 имеет знак минус и передаточные отношения
имеет знак минус и передаточные отношения 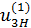 и
и  редукторов определяется по формуле
редукторов определяется по формуле