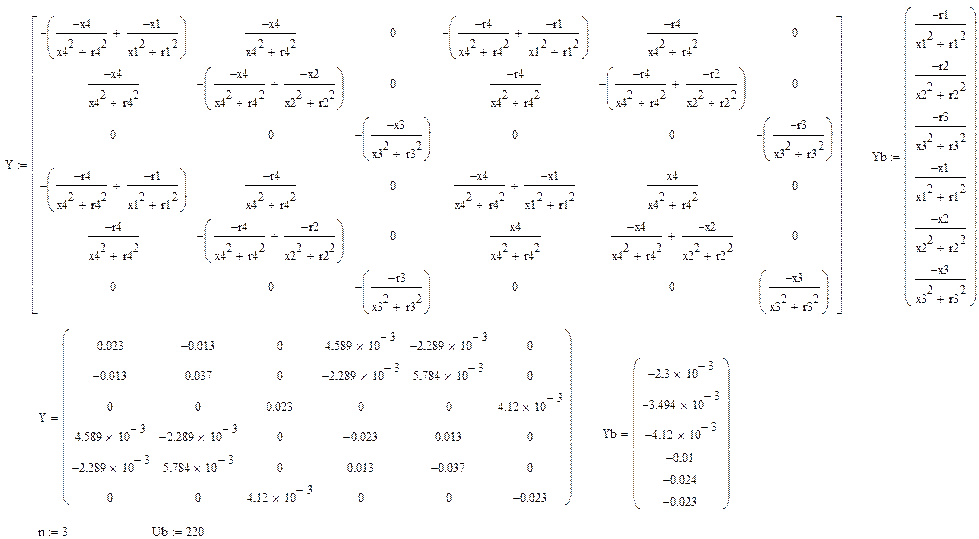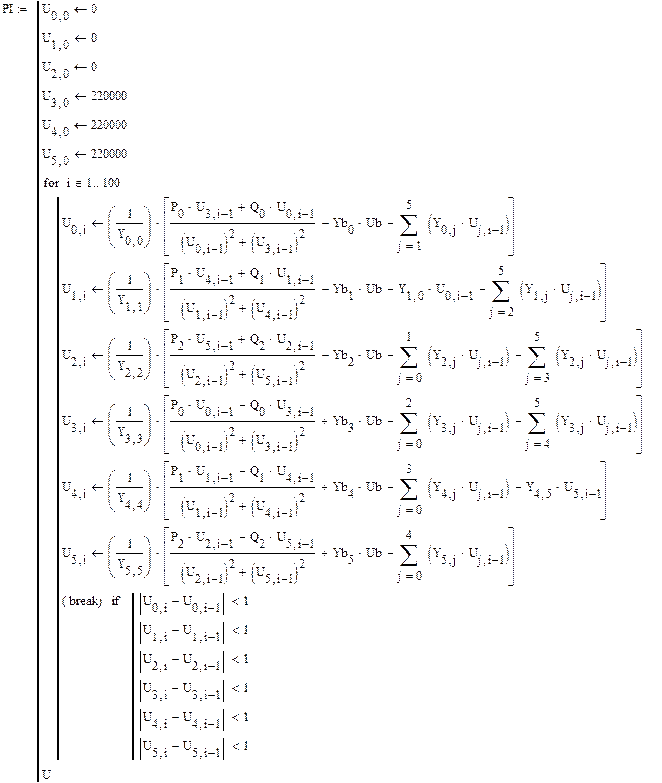|
|
Теоретическая часть курсовой работыВведение - Основной целью курсового проектирования является приобретения навыков расчета и проектирования электроэнергетических систем и сетей с применением ЭВМ. Курсовой проект состоит из пояснительной записки и программы расчета узловых напряжений на ЭВМ одним из методов, предложенных преподавателем согласно варианту. Пояснительная записка должна включать: титульный лист, содержание, задание на курсовое проектирование теоретическое описание метода с перечислением его достоинств и недостатков, схема замещения участка электрической сети, предложенного преподавателем согласно варианту, аналитический расчет в матричном виде, численный расчет в матричном виде (по результатам работы программы, составленной студентом), окончательный ответ (узловые напряжения в виде матрицы-столбца), распечатка программы для ЭВМ, список используемой литературы. Варианты заданий Темами курсового проекта могут быть тем: -Решение системы узловых уравнений методом простой итерации; - Решение системы узловых уравнений методом Гаусса; - Решение системы узловых уравнений методом Зейделя; - Решение системы узловых уравнений методом Ньютона. Для Э-323н: Номер варианта схемы соответствует номеру ФИО студента в списке группы на 01.02.2016, алгоритмическая основа для программы – для всех – метод Гаусса. Для Э-323сф: Номер варианта схемы соответствует номеру ФИО студента в списке группы на 01.02.2016, алгоритмическая основа для программы – для всех – метод простой итерации. Для Э-323с: Номер варианта схемы соответствует номеру ФИО студента в списке группы на 01.02.2016, алгоритмическая основа для программы – для всех – метод Зейделя. Если № ФИО студента в списке>30, № варианта=№ФИО‒30. Заданные параметры Активные и реактивные сопротивления r1….r6, x1….x6 и напряжение в базисном узле (Uб = 220 кВ) заданы в программе. Активные и реактивные мощности нагрузок в узлах запрашиваются программой P1…P3, Q1…Q3 Искомые параметры Мнимые и действительные части узловых напряжений U’1…U’3, U’’1…U’’3 Исходная схема
Варианты заданий
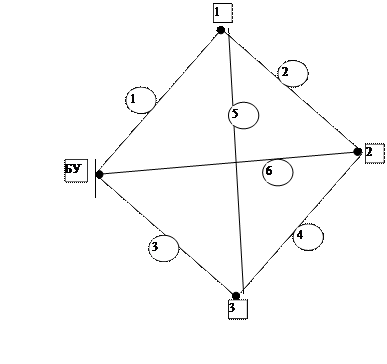
Задание 1. Нарисовать граф схемы по варианту 2. В соответствии с вариантом сделать аналитическую и численную записи системы нелинейных уравнений узловых напряжений в матричной форме, включая матрицу узловых проводимостей (размер 6×6), столбцы узловых напряжений, задающих узловых токов и взаимных проводимостей между базисным узлом и независимыми. При аналитической записи в матрице и столбце проводимостей расписать каждый элемент, например
3. Решить систему нелинейных уравнений узловых напряжений (методом в соответствии с вариантом) и определить мнимые и действительные части узловых напряжений, применяя индивидуально разработанную программу ЭВМ.
Пример решения варианта X методом простой итерации и методом Зейделя (при выполнении курсовой работы по дисциплине «Применение ЭВМ», срок сдачи до июня).
1.вычисление сопротивлений ветвей, задание активных и реактивных мощностей. В данном примере столбцы P и Q соответствуют активным и реактивным мощностям в каждом из трех узлов схемы варианта в МВт/МВАр, знак минус перед цифрой указывает, что задается нагрузка (а не источник мощности)
2.составление матриц узловых проводимостей Y и базисных проводимостей Yb Правила заполнения матрицы узловых проводимостей. Матрица узловых проводимостей для уравнений узловых напряжений, приведенных к системе действительных уравнений, это квадратная матрица с числом строк и столбцов 2 n, где n – число узлов без базисного (в данном примере 3 независимых узла и, соответственно, матрица узловых проводимостей будет иметь размер 6×6). Матрица Y состоит из четырех квадратных подматриц размером 3×3
где
Каждая строка, как и каждый столбец всех подматриц, соответствуют одному из узлов. На главной диагонали каждой подматрицы находятся собственные узловые проводимости равные сумме проводимостей ветвей, соединенных с данным узлом. Прочие, недиагональные элементы – взаимные узловые проводимости, равны взятой с обратным знаком проводимости ветви, соединяющей два узла, соответствующих номерам строки и столбца подматрицы, на пересечении которых находится данный элемент. Если какие-либо два узла не соединены непосредственно, позиция на пересечении соответствующих им строки и столбца подматрицы заполняется нулем. Активная проводимость ветви равна отношению ее активного сопротивления к сумме квадратов ее активного и реактивного сопротивлений, реактивная проводимость – отношение реактивного сопротивления к сумме квадратов ее активного и реактивного сопротивлений. Матрица взаимных проводимостей между базисным узлом и независимыми Yb – представляет собой столбец, содержащий в данном случае 6 элементов, где верхние три элемента взаимные активные проводимости между базисным узлом и независимыми, нижние три элемента – взаимные реактивные проводимости. Пример матриц Y и Yb для схемы на рисунке приведены ниже
3. Составление программы реализующей алгоритм метода Зейделя (Гаусса или простой итерации, в зависимости от варианта задания) для расчета узловых напряжений. Программа носит универсальный характер и применима для любого варианта схемы. Для приведенного ниже примера: PI – название программы (в алгоритмической основе - метод простой итерации), строки таблицы после знака равно соответствуют напряжением в узлах (первые три строки – мнимым частям узловых напряжений, следующие три строки – действительным частям узловых напряжений), столбцы – значениям узловых напряжений на каждом шаге итерационного процесса метода простой итерации, первый столбец соответствует начальным, произвольно заданным приближениям узловых напряжений (рекомендуется задавать начальные приближения мнимых частей узловых напряжений равными нулю, действительных частей – равными напряжению в базисном узле = 220 кВ), последний столбец соответствует решению т.е. значениям мнимых и действительных частей узловых напряжений на последнем шаге итерационного процесса, на котором достигнута его сходимость. Далее приведены программы реализующие алгоритмы методов Гаусса и Зейделя.
4. Утяжеление режима. Вычислить узловые напряжения, увеличивая нагрузку в одном из узлов (например, в первом) до тех пор, пока напряжение не выйдет за пределы нормально допустимых значений (±5% от номинального напряжения) (209-231 кВ для данной ступени напряжения). Построить в MS Excel соответствующие таблицу и график. Вернуться к исходным значениям нагрузок в узлах и аналогично произвести утяжеление режима увеличением нагрузки в узле 2. Вернуться к исходным значениям нагрузок в узлах и аналогично произвести утяжеление режима увеличением нагрузки в узле 3. Представить результат в виде, соответственно, трех таблиц и трех графиков.
Подробнее о составлении программ для курсовой Пр. ЭВМ и РГР по ЭМС смотри в файле MATHCAD для курсовой Теоретическая часть курсовой работы 1.Теоретическое описание метода расчета примененного в алгоритмической основе программы ЭВМ для решения системы нелинейных уравнений узловых напряжений (метод простой итерации, Гаусса или метод Зейделя – по варианту) (см. Итерационные методы решения (теория) и учебное пособие Примение ЭВМ в энергетике в эл. виде)
12 |
|
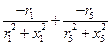

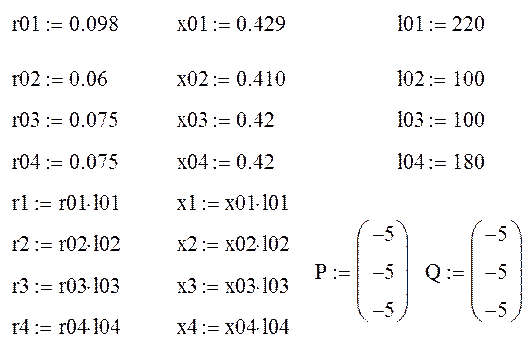
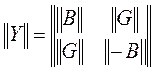 ,
,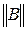 - подматрица реактивных проводимостей размером 3×3,
- подматрица реактивных проводимостей размером 3×3, - подматрица активных проводимостей размером 3×3.
- подматрица активных проводимостей размером 3×3.