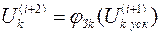|
|
Применение метода Гаусса для решения нелинейных уравнений узловых напряженийНелинейные уравнения узловых напряжений в форме балансов токов имеют особенность: они линейны слева и нелинейны справа, т.е. все элементы схемы замещения линейны, кроме источников тока. Т.к. нелинейность токов справа, то возможно применение метода Гаусса и метода обратной матрицы для решения этой задачи. 1) Применение метода Гаусса При решении нелинейной системы уравнений узловых напряжений в форме баланса токов метод Гаусса может использоваться на каждом шаге итерационного процесса, считая нелинейную систему линейной на данном шаге Алгоритм - зададим начальное приближение узловых напряжений и определим правые части нелинейной системы Правая часть системы нелинейных уравнений узловых напряжений в форме баланса токов при подстановке
Считая, что токи постоянны и определяются приближениями, в таком случае система нелинейных уравнений превращается в систему линейных алгебраических уравнений, которую можно рассчитать методом Гаусса.
Линейная система решается методом Гаусса
Решение методом Гаусса дает столбец новых приближений Решив линейную систему методом Гаусса, получаем новое приближение узловых напряжений и переходим к этапу два: определению кривых нелинейных частей системы узловых уравнений при подстановке новых приближений узловых напряжений.
Далее находятся вектора приближения узловых напряжений решением нелинейной системы методом Гаусса и так далее, до тех пор, пока итерационный процесс не сойдется. Таким образом, каждый шаг итерационного процесса методом Гаусса включает два этапа: 1) определение нелинейных правых частей системы уравнений при подстановке приближений узловых напряжений, найденных на предыдущей итерации 2) решение линейной системы методом Гаусса и определение следующих приближений: Каждый 1) 2)
Применение метода простой итерации и метода Зейделя для решения системы нелинейных уравнений Узловых напряжений
где
Линейный случай метода простой итерации
Нелинейный случай метода простой итерации
где Отличие заключается в том, что вместо постоянной величины
Применение метода Зейделя Метод Зейделя: линейный случай
Метод Зейделя: нелинейный случай
где При расчете на ЭВМ комплексные переменные заменяются действительными и по методу Зейделя вычисляются действительные и мнимые части узловых напряжений.
Ускоренный метод Зейделя Для ускорения сходимости метода Зейделя используется ускоряющий коэффициент
где Ускоряющий коэффициент находится в пределах от 0 до 1, если ускоряющий коэффициент равен единице, то это обычный метод Зейделя.
Список литературы 1.Основная литература 1. Идельчик В.И. Электрические системы и сети. М.: Альянс, 2009 2.Зарудский Г.К., Кутлер П.П. Особенности расчетов нормальных режимов электропередач сверхвысокого напряжения. – М.:ИПКгосслужбы, 2005. 3.Азаров В.С. Передача и распределение электроэнергии в примерах и решениях. М.: МГОУ, 2005. 4.Исмагилов Ф.Р., Максудов Д.В. Расчеты на ЭВМ установившихся режимов электроэнергетической системы. Уфа, Изд-во УГАТУ, 2008. 5.Исмагилов Ф.Р. Максудов Д.В. Оптимизация установившихся режимов электроэнергетической системы. Уфа, Изд-во УГАТУ, 2008.
2. Дополнительная литература 1. Хемди А. Таха. Глава 3. Симплекс-метод // Введение в исследование операций. М.: «Вильямс», 2007. — С. 95-141. 2. Томас Х. Кормен и др. Глава 29. Линейное программирование // Алгоритмы: построение и анализ— 2-е изд. — М.: «Вильямс», 2006. — С. 1296. 3. Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Высшая математика для экономистов / Под ред. Н. Ш. Кремера. — 3-е изд. — М.: ЮНИТИ-ДАНА, 2007. — 479 с. 4. Куликов, Ю. А. Переходные процессы в электрических системах: учеб. пособие / Ю. А. Куликов. - Изд. 2-е» испр. и доп. - Новосибирск: Изд-во НГТУ, 2006. - 284 с.
12 |
|
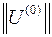 ;
;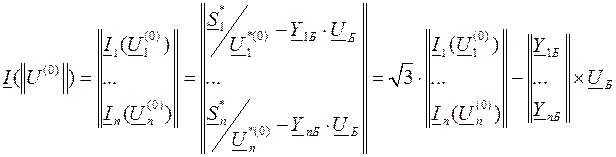
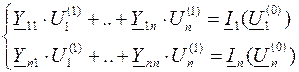
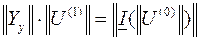
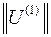 .
.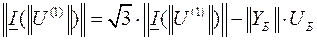
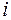 -ый итерационный шаг итерационного процесса с применением на каждом шаге метода Гаусса для решения линейной системы уравнений:
-ый итерационный шаг итерационного процесса с применением на каждом шаге метода Гаусса для решения линейной системы уравнений: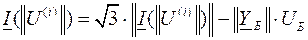
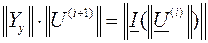
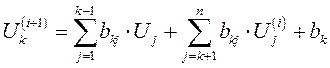
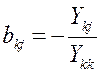 , при
, при 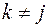
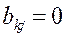 , при
, при 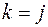
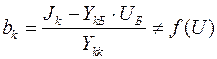
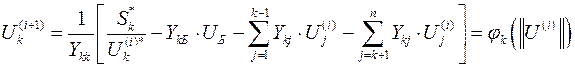
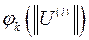 - нелинейная функция, описывающая итерационный процесс по методу простой итерации
- нелинейная функция, описывающая итерационный процесс по методу простой итерации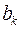 принимается нелинейная известная часть системы уравнений, зависящая от напряжений и изменяется от итерации к итерации.
принимается нелинейная известная часть системы уравнений, зависящая от напряжений и изменяется от итерации к итерации.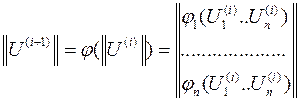
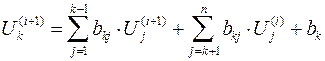
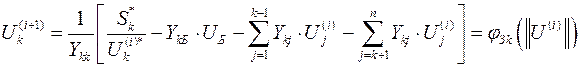
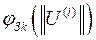 - нелинейная функция, описывающая итерационный процесс по методу Зейделя.
- нелинейная функция, описывающая итерационный процесс по методу Зейделя.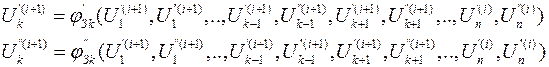
 ,
, 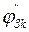 - составляющие
- составляющие ,
,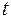 - ускоряющий коэффициент,
- ускоряющий коэффициент, 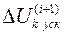 - поправка k-го узлового напряжения на (i+1) шаге.
- поправка k-го узлового напряжения на (i+1) шаге.