|
|
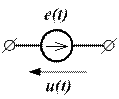
Электрические линейные цепи: элементы, схемы, законы, классификацияТеория электрических цепей исходит из приближённой замены реального электроэнергетического устройства идеализированной схемой замещения - электрической цепью. Электрической цепью называют совокупность элементов, образующих пути для протекания электрического тока, а также источников ЭДС или (и) тока. В теории электрических цепей предполагаются идеализированные источники электрической энергии: идеальные источники ЭДС и/или идеальные источники тока, а также идеализированные потребители (пассивные элементы): резистор (сопротивление), конденсатор, катушка индуктивности. Эти потребители представляют собой минимальный набор простейших элементов, с помощью комбинаций которых можно описывать все реальные элементы энергосистемы. Конденсатор может запасать энергию электрического поля, катушка индуктивности – энергию магнитного поля, а резистор только выделяет тепловую энергию при протекании тока в соответствие с законом Джоуля-Ленца (других простейших элементов нет). Электрическую установку можно представить как электрическую цепь в тех случаях, когда напряжение между её узлами равно разности между их потенциалами. В этом разделе все элементы предполагаем линейными – их параметры не зависят от величины приложенного напряжения (ток и напряжение связаны линейно – закон Ома). Свойства конденсатора и катушки индуктивности полностью описываются на языке токов и напряжений, возникающих на их зажимах; при этом игнорируется сложность полей внутри этих элементов. То, что происходит внутри, отделяется от того, что происходит снаружи. Что происходит внутри элементов можно описать только на языке уравнений Максвелла. Идеальный источник ЭДС (или напряжения) представляет собой активный элемент с двумя зажимами; его внутреннее сопротивление стремится к нулю, а напряжение не зависит от тока, проходящего через источник (рис.8.1).
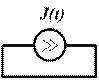
Рисунок 8.1. Идеальный источник ЭДС ЭДС источника создаётся за счёт действия сторонних сил. Напряжение на зажимах равно его ЭДС, т.е. Идеальный источник тока представляет собой активный элемент, ток через который не зависит от величины подключённой нагрузки (рис.8.2).
Рисунок 8.2. Идеальный источник тока С увеличением сопротивления нагрузки растёт напряжение на зажимах источника тока, поэтому источник тока не может работать с разомкнутой нагрузочной цепью. На рис.8.2 это отражено шунтированием нагрузочной цепи. Подключение источника тока к цепи производится дешунтированием ключа. Внутреннее сопротивление источника тока стремится к бесконечности. Сопротивление. Сопротивлением охарактеризуется любой проводник длиной
где
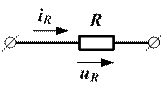
а) б) Рисунок 8.3. Идеальное активное сопротивление Линейная связь между током и напряжением определяется выражением
Выражение (8.1) носит название закона Ома, а произведение мгновенных значений напряжения и тока Катушка индуктивности. Катушка индуктивности (индуктивный элемент) (рис.8.4, а) запасает энергию магнитного поля
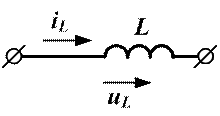
а) б) Рисунок 8.4. Идеальная катушка индуктивности Идеальная индуктивность не обладает ни активным сопротивлением, ни ёмкостью. Линейная связь между напряжением и производной тока в индуктивности определяется выражением
Конструктивно индуктивность часто выполняется из изолированного провода, намотанного в виде спирали (рис.8.4, а). Ток Интегрально его можно охарактеризовать потоком
для каждого витка через поверхность Конденсатор. Конденсатор (ёмкостной элемент) запасает энергию электрического поля
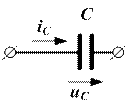
Наиболее часто конденсатор выполняется в виде двух металлических пластин, разделённых слоем диэлектрика (рис.8.5, а). Собственно ёмкость, для использования которой и предназначен этот элемент, представляет собой отношение двух равных по значению, но противоположных по знаку зарядов пластин, разнесённых в пространстве, к напряжению этого элемента
а) б) Рисунок 8.5. Идеальный конденсатор Единицей ёмкости является фарада - 1 Ф = 1 Кл/1 В. Ёмкостью обладает не только специально изготовленный конденсатор, но и пары проводов электропередач, система провод - земля и т.д. При составлении схемы замещения реальной цепи необходимо отражать подобные связи ёмкостными элементами, входящими в схему наравне с конденсаторами. Условное обозначение конденсатора показано на рис. 8.5, б. Идеальный конденсатор не обладает ни активным сопротивлением, ни индуктивностью. Линейная связь тока элемента с производной напряжения определяется выражением
Таким образом, любая электрическая цепь может быть реализована, используя перечисленные выше элементы: резистор, конденсатор, катушка индуктивности. Электрические цепи изображают в виде чертежа, называемого схемой электрической цепи. Такая схема составляется из условных обозначений элементов цепи (рис. 8.3 - 8.5) и показывает их соединение. Последовательность элементов, по которым протекает один и тот же ток, называется ветвью; точка соединения ветвей называется узлом; замкнутый путь, проходящий по нескольким элементам, называется контуром. Решить задачу анализа (расчёта) цепи это значит, при заданных значениях параметров элементов схемы и источников ЭДС и тока рассчитать неизвестные токи и напряжения ветвей. Решение задачи анализа заключается в составлении полной системы уравнений цепи и её решении. Для составления уравнений цепи пользуются правилами Кирхгофа. Первое правило Кирхгофа записывается для узла цепи: алгебраическая сумма токов в узле, равна нулю:
При составлении уравнений по первому правилу Кирхгофа необходимо задаться условно-положительными направлениями токов, обозначив их стрелками. Если стрелки токов направлены от узла, то записываются со знаком «+», направленные к узлу – со знаком «–» (хотя можно и наоборот). Второе правило Кирхгофа записывается для контура цепи: алгебраическая сумма напряжений на всех элементах любого замкнутого контура равна сумме ЭДС данного контура:
При записи уравнений по второму правилу Кирхгофа необходимо выбрать независимые контуры и их направление обхода. Независимым является такой контур, в котором имеется хотя бы одна ветвь, не входящая в другие контуры (для цепей без источников тока). Направление обхода всех контуров рекомендуется выбирать по часовой стрелке (хотя можно для каждого контура выбирать произвольно). Знаки напряжений устанавливаются следующим образом: если направление напряжений (направление стрелки напряжения элемента ветви определяется направлением тока в нём) и ЭДС совпадают с направлением обхода контура, то принимают знак «+» и наоборот. Система уравнений цепи должна быть полной, но не избыточной. Если число ветвей схемы равно В, а число узлов У, то число независимых уравнений, которые можно составить по первому правилу Кирхгофа, равно У – 1, по второму - В – У + 1 . Число уравнений, составленных по первому и второму правилам Кирхгофа, равно числу ветвей схемы В=У – 1 + В – У + 1, при этом необходимо также использовать соотношения (8.1) – (8.3). В общем случае решение задачи анализа сложной электрической цепи (т.е. задачи определения всех неизвестных токов и напряжений её элементов при известной схеме и параметрах - сопротивлениях, ёмкостях, индуктивностях, ЭДС и источников тока) оказывается достаточно сложным, поэтому часто используют различные преобразования схем. Значительно проще задача анализа решается, когда источники энергии являются постоянными или синусоидальными. Электрические цепи подразделяют на: цепи постоянных токов (если токи и напряжения всех элементов цепей не изменяются во времени) и цепи переменных токов (если токи и напряжения всех элементов цепей изменяются во времени) и, в частности, цепи синусоидальных токов (если эти токи и напряжения цепей изменяются во времени по синусоидальным законам). Электромагнитные процессы электрических цепей принято делить на установившиеся, когда токи и напряжения всех элементов цепи описываются периодическими функциями времени (как, например, в цепях постоянного и синусоидального токов), и переходные. Последними называются процессы перехода от одного установившегося состояния к другому. Установившиеся процессы принято называть режимами; так, говорят о режиме постоянного тока и режиме синусоидального тока. Далее рассмотрены только установившиеся режимы. 8.2. Цепи постоянного тока В схемах замещения цепей постоянных токов отсутствуют ёмкостные и индуктивные элементы. Из допущения о постоянстве тока из уравнения (8.2) для индуктивного элемента следует, что напряжение его будет равным нулю, т.е. сам индуктивный элемент в схеме замещения цепи на постоянном токе представляет собой идеальный проводник с нулевым сопротивлением - так называемую «закоротку». Из допущения о постоянстве напряжения для ёмкостного элемента из уравнения (8.3) следует, что его ток в этом случае будет равен нулю, а сам ёмкостной элемент представляет собой «разрыв» ветви цепи. Полученная резистивная цепь описывается уже не дифференциальными, а алгебраическими уравнениями. Для расчёта электрической цепи предварительно по по 1-му и 2-му правилам Кирхгофа составляется система уравнений с учётом указанных выше замечаний. Токи в цепи распределяются таким образом, что выделяемая во всех элементах цепи минимальна – принцип - минимума для электрической цепи. Пример 8.1. Составим систему уравнений по правилам Кирхгофа для электрической цепи постоянного тока, приведенную на рис.8.6. Число ветвей схемы равно шести, поэтому полная система уравнений схемы должна состоять из шести уравнений. Рекомендуется сопротивление и ЭДС одной ветви обозначать одним индексом. Произвольно выберем положительные направления токов. Заданная схема содержит 4 узла, поэтому по первому правилу Кирхгофа можно составить 3 независимых уравнения:
Рисунок.8.6. Электрическая схема к примеру 8.1 Три недостающих уравнения составим по второму правилу Кирхгофа для трёх независимых контуров (направление обхода по часовой стрелке):
Таким образом, система уравнений цепи состоит из 6 независимых уравнений. |
|
 .
.
 и сечением
и сечением  (рис. 8.3, а), причём если ток распределён по сечению проводника равномерно, то
(рис. 8.3, а), причём если ток распределён по сечению проводника равномерно, то ,
, - удельное электрическое сопротивление, характеризующее свойства материала проводника. Для цепей постоянного тока и переменного с частотой 50 Гц, пренебрегая поверхностным эффектом, величину сопротивления считают одинаковой. В схеме замещения электрической цепи резистивные элементы отражают не только собственно резисторы, но и сопротивления проводов линий электропередач, сопротивления проводников, из которых выполнены обмотки трансформаторов, электрических машин и т.п. Идеальное активное сопротивление (резистор) не обладает ни индуктивностью, ни ёмкостью (рис. 8.3, а).
- удельное электрическое сопротивление, характеризующее свойства материала проводника. Для цепей постоянного тока и переменного с частотой 50 Гц, пренебрегая поверхностным эффектом, величину сопротивления считают одинаковой. В схеме замещения электрической цепи резистивные элементы отражают не только собственно резисторы, но и сопротивления проводов линий электропередач, сопротивления проводников, из которых выполнены обмотки трансформаторов, электрических машин и т.п. Идеальное активное сопротивление (резистор) не обладает ни индуктивностью, ни ёмкостью (рис. 8.3, а).

 . (8.1)
. (8.1) , называемое мгновенной мощностью, для резистора
, называемое мгновенной мощностью, для резистора 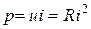 (закон Джоуля - Ленца). Мощность в данном случае определяет количество теплоты, выделяемое резистором в единицу времени. Резистор является диссипативным элементом, в нём растрачивается (диссипирует) электрическая энергия. Таким образом, резистор - это элемент, предназначенный для использования его электрического сопротивления. Единицей сопротивления является Ом - 1 Ом = 1 В/1 А (проводимости
(закон Джоуля - Ленца). Мощность в данном случае определяет количество теплоты, выделяемое резистором в единицу времени. Резистор является диссипативным элементом, в нём растрачивается (диссипирует) электрическая энергия. Таким образом, резистор - это элемент, предназначенный для использования его электрического сопротивления. Единицей сопротивления является Ом - 1 Ом = 1 В/1 А (проводимости  - сименс - 1 См= 1 А/1 В), мгновенной мощности - ватт - 1 Вт = 1 В · 1 А. Условное обозначение резистора показано на рис. 8.3,б.
- сименс - 1 См= 1 А/1 В), мгновенной мощности - ватт - 1 Вт = 1 В · 1 А. Условное обозначение резистора показано на рис. 8.3,б. , скорость изменения которой определяет её мгновенную мощность
, скорость изменения которой определяет её мгновенную мощность .
.
 . (8.2)
. (8.2) в этом случае создаёт магнитное поле, направление индукции
в этом случае создаёт магнитное поле, направление индукции  которого связано с направлением тока правилом правого винта.
которого связано с направлением тока правилом правого винта.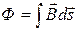
 катушки называется потокосцеплением
катушки называется потокосцеплением  . Индуктивность характеризует связь между этим потокосцеплением и вызывающим его током
. Индуктивность характеризует связь между этим потокосцеплением и вызывающим его током  . Единицей магнитной индукции является тесла - 1 Тл = 1 Вб · 1 м2, индуктивности - генри - 1 Гн = 1 Тл/1 А. Таким образом, индуктивная катушка - это элемент цепи, предназначенный для использования его индуктивности. Индуктивностью помимо специально изготовляемых катушек обладают и другие элементы реальных электрических цепей, в частности провода линий электропередач, что необходимо отражать в схемах замещения соответствующих цепей. Условное обозначение индуктивности показано на рис. 8.4,б.
. Единицей магнитной индукции является тесла - 1 Тл = 1 Вб · 1 м2, индуктивности - генри - 1 Гн = 1 Тл/1 А. Таким образом, индуктивная катушка - это элемент цепи, предназначенный для использования его индуктивности. Индуктивностью помимо специально изготовляемых катушек обладают и другие элементы реальных электрических цепей, в частности провода линий электропередач, что необходимо отражать в схемах замещения соответствующих цепей. Условное обозначение индуктивности показано на рис. 8.4,б. , скорость изменения этой энергии во времени его характеризует мгновенную мощность
, скорость изменения этой энергии во времени его характеризует мгновенную мощность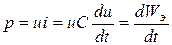 .
.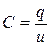

 . (8.3)
. (8.3)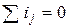 . (8.4)
. (8.4) . (8.5)
. (8.5) (для узла I)
(для узла I)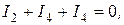 (для узла II)
(для узла II) (для узла IV)
(для узла IV)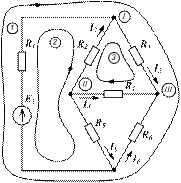
 (для контура 1)
(для контура 1) (для контура 2)
(для контура 2) (для контура 3)
(для контура 3)