|
|
Определение положения нейтральной оси.СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
М Е Т О Д И Ч Е С К И Е У К А З А Н И Я
к выполнению контрольных работ по сопротивлению материалов для студентов заочной формы обучения строительных специальностей. Часть2. Сложное сопротивление. Кривой брус. Устойчивость. Удар.
Брянск 2011
доцент, к.т.н. В.М. Захаров
Рецензент: доцент, к.т.н., зав. кафедрой СК БГИТА С.Г. Парфенов
Рекомендованы учебно-методической комиссией строительного факультета Протокол от .
К ЗАДАЧЕ № 8 ВНЕЦЕНТРЕННОЕ СЖАТИЕ Короткий чугунный стержень, поперечное сечение которого изображено на рисунке 8.1, сжимается продольной силой Р, приложенной в точке А. Требуется: 1.Выразить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении через силу Р и размеры сечения. 2.Найти допускаемую нагрузку [Р] при допускаемых напряжениях для чугуна на сжатие [σс]=1000 МПа (кгс/см2) и на растяжение [σр]= 300 МПа (кгс/см2) . 3.Определить положение нейтральной оси и построить эпюру напряжений вдоль линии, перпендикулярной к нейтральной оси,
В общем случае внецентренного сжатия, когда точка приложения силы Р не лежит ни на одной ив главных осей инерции, через каждое поперечное сечение стержня передаются продольная сила М=-Р и изгибающие моменты Мх=Р·хР и Му=Р·уР (рисунок 8.1в), то есть внецентренное сжатие стержня можно представить комбинацией центрального сжатия и косого изгиба. Напряжение в произвольной точке поперечного сечения с координатaми x и у для рассматриваемого случая внецентренного сжатия определяется по формуле: σ= =- Так как это уравнение плоскости, то максимальные напряжения будут в точках, наиболее удаленных от нейтральной оси, уравнение которой имеет вид: : (1 + Здесь x и у - координаты точек нейтральной оси; xР и уР - координаты точки приложения силы Р (точки А); Jх и Jу - главные центральные моменты инерции сечения; iх и iу - радиусы инерции относительно глазных центральных осей. Провести нейтральную ось можно, вычислив координаты точек, в которых она пересекает главные центральные оси по формулам: ax = -
Можно поступить иначе. Поскольку нас интересует лишь направление нейтральной осн. можно определить угол ее наклона по отношению к оси X по формуле, известной из теории косого изгиба: tg α = tg φ · Здесь tg φ = xP/уP, определяющий направление силовой линии ОА по отношению к оси У, нам известен. В нашем примере без определения направления нейтральной оси можно определить лишь точку, в которой возникает наибольшее сжимающее напряжение (это точка 1). Наибольшее же растягивающее напряжение возникает либо в точке 2, либо в точке 3, в зависимости от того, какая из них окажется более удаленной от нейтральной оси (рисунок 8.1а). Определение положения центра тяжести сечения Центр тяжести "О" лежит на оси X, являющейся осью симметрии сечения. Вспомогательной осью для определения положения центра тяжести на этой оси выбираем ось У. Площадь сечения: F = F1 + F2 = 3·8 + 6·4 = 24 + 24 = 48 см2. Статический момент относительно оси y1: Sy1 = F1·0 + F2·x1c2 = F·x1(0), откуда x1(0) =
Рисунок 8.1, Вычисление главных центральных моментов и радиусов инерции. Главными центральными осями являются: ось X и перпендикулярная к ней ось У. JХ = JIx1 + JIIx2 = Jy = JIy1+ F1·m12 + JIIy2+ F2·m22 +
ix2 = Определение положения нейтральной оси. а) Определяем отрезки, отсекаемые нейтральной осью на главных осях по формулам (8.3): ay = - ax = - Знак минус означает, что эти отрезки следует отложить в сторону, противоположную выбранным направлениям отсчетов координат. Чем ближе расположена точка приложения силы к центру тяжести сечения, тем дальше от центра отодвигается нейтральная ось, т.е. тем меньше становится зона растяжения. б) Определяем направление нейтральной оси по формуле (8.4) (в этом случае не нужно вычислять ix, iy, ах и ау): tg φ = tg α = tg φ · α = 10° 13'. 8.4. Определение опасных точек, запись условий прочности и определение допускаемой нагрузки. По построению (рисунок 8.1а) видно, что наиболее удаленными от нейтральной оси являются точки 1 (х=3,75 см; у=4 см) и 2 (х=0.75 см; у=-4 см). В т. 1, как уже отмечалось, возникает наибольшее сжимающее напряжение. В т. 2 возникает растягивающее напряжение, большее, чем в т. 3, несмотря на то, что в ней растяжение создает лишь момент Мх, а в т. 3 возникает растяжение от обоих моментов (см. рис. 8.1в). Условия прочности: а) на сжатие: max σс = | σ1 | =
P1 · 793 ≤ 100·106, откуда P1 ≤ б) на растяжение:
P2 · 275 ≤ 30·106, откуда P2 ≤ Из найденных двух значений берем меньшее. Итак, [P]= 109 кН. Построение эпюры напряжений Построение эпюры напряжений вдоль линии, перпендикулярной к нейтральной оси, показано на рисунке 8.1б. Его можно выполнить различными способами. Одной из ординат эпюры является отрезок, пропорциональный напряжению max σр = σ2 = 30 МПа. В качестве второй точки для проведения эпюры может служить либо нулевая точка, принадлежащая нейтральной оси, если таковая определялась (пункт 8.За), либо ордината, соответствующая напряжению в центре тяжести сечения σ0 = - P/F = 109000/(48·10-4) = =- 22,8·106 Па = - 22,8 МПа (- 228 кгс/см2), если определялось лишь направление нейтральной оси (пункт 8.Зб). Наибольшее сжимающее напряжение max σс определится на эпюре автоматически, но для контроля его можно вычислить, используя данные пункта 8.4а. max σс = σ1 =109000·793 = 86,9 ·106Па = 86,9 МПа (869 кгс/см2), На рисунке 8.1г показана пространственная эпюра напряжений в.поперечном сечении стержня. Для ее построения ординаты, соответствующие всем угловым точкам, взяты по эпюре, показанной на схеме 8.1б. Конечно, их можно подсчитать также по формуле (8.1). σ3 = -
σ4 = -
σА = -
σ5 = -
σ6 = -
σ7 = -
К ЗАДАЧЕ № 9 |
|
 -
-  -
-  = -
= -  -
-  -
- 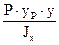 =
= +
+  ). (8.1)
). (8.1) ; ay = -
; ay = -  . (8.3)
. (8.3) . (8.4)
. (8.4) =
=  =
=  = 2,25 cm.
= 2,25 cm.



 +
+  = 128 + 32 = 160 см4.
= 128 + 32 = 160 см4. + 24·2,252 +
+ 24·2,252 +  + 24·2,252 = 333 см4.
+ 24·2,252 = 333 см4. =
=  = 3,34 см2; iy2 =
= 3,34 см2; iy2 =  =
=  = 6,95 см2
= 6,95 см2 = - 1.57 см.
= - 1.57 см. = - 9.28 см.
= - 9.28 см. =
=  = 0б375;
= 0б375; = 0,180;
= 0,180; (1 +
(1 +  +
+  ) ≤[σ],
) ≤[σ], (1 +
(1 +  +
+  ) ≤ 100·106,
) ≤ 100·106, = 126000 Н = 126 кН (12600 кгс);
= 126000 Н = 126 кН (12600 кгс); (1 +
(1 +  +
+  ) ≤[σ],
) ≤[σ],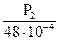 (1 +
(1 +  +
+  = 109000 Н = 109 кН (10900 кгс);
= 109000 Н = 109 кН (10900 кгс); +
+  ) =
) =  (1 +
(1 +  +
+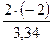 ) = 17,4·106 Па = 17,4 МПа (174 кгс/см2);
) = 17,4·106 Па = 17,4 МПа (174 кгс/см2); +
+  ) =
) =  ) = -37,2·106 Па = -37,2 МПа (-372 кгс/см2);
) = -37,2·106 Па = -37,2 МПа (-372 кгс/см2);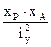 +
+  ) =
) =  +
+ +
+  ) =
) =  +
+  ) =
) =  +
+ ) = 24,4·106 Па = 24,4 МПа (244 кгс/см2);
) = 24,4·106 Па = 24,4 МПа (244 кгс/см2); +
+  ) =
) =