|
|
Напряжения, связанные с изгибающим моментома) в наружных волокнах: yнар = ρнар = R + (σM)нар =
б) во внутренних волокнах:
yвн = -( ρвн = R - (σM)вн =
Напряжения, связанные с продольной силой
σN =
Суммарные напряжения в наружных волокнах σнар = - M∙0.00850 + Суммарные напряжения во внутренних волокнах σвн = M∙0.01246 + Результаты вычислений для трех сечений приведены в таблице Таблица 10.3
Рисунок 10.7
Как видно из таблицы, наибольшими являются напряжения во внутренних точках сечения «С» участка АС, т. е. опасным в данном случае является сечение «С»участка АС,несмотря на то, что абсолютное значение продольной силы в этом сечении меньше, чем в сечении «С»участка ВС,при равных изгибающих моментах. Эпюра нормальных напряжений для опасного сечения приведена на рисунке 10.7 справа. Здесь же штриховой прямой показана эпюра нормальных напряжений в соответствующем прямом брусе, для которого напряжения в крайних волокнах, связанные с изгибающим моментом, вычислены по формуле (10.11): max σМпр = ± 10.3.2. Прямоугольное сечение (рисунок 10.8) Основные размеры: b = 6 см; h=10 см; ρнар = 25 см; ρвн=15см. Определение положения нейтральной оси. Как и в предыдущем примере, брус имеет очень большую кривизну (R:h = 20:10 = 2<<3). Поэтому нужно пользоваться точной формулой для радиуса кривизны нейтрального слоя: r = yo = R – r = 20 – 19,576 = 0,424 см. Для сравнения определим уoпо приближенной формуле (10.10). Площадь сечения: F = b∙h = 6∙10 = 60 см2. Главный центральный момент инерции: Ix = yo ≈ Напряжения, связанные с изгибающим моментом: а) в наружных волокнах: yнар = ρнар = R + (σM)нар = б) во внутренних волокнах: yвн = -( ρвн = R - (σM)вн =
Рисунок 10.8
Напряжения, связанные с продольной силой
σN = Суммарные напряжения в наружных волокнах σнар = - M∙0.00853 +
Суммарные напряжения во внутренних волокнах σвн = M∙0.0120 + Результаты вычислений для трех сечений приведены в таблице.
Таблица 10.4
Как видно из таблицы, в данном случае опасным оказалось сечение «К»,несмотря на то, что абсолютные величины изгибающего момента и продольной силы в этом сечении меньше, чем в сечении «С»участка ВС. Эпюра нормальных напряжений для сечения «К»построена на рисунке 8 справа. Для сравнения здесь же показана {штриховой прямой) эпюра нормальных напряжений в прямом брусе. Наибольшие напряжения σМпр для этой эпюры вычислены по формуле (11.16): max σМпр = ± 10.3.3. Сечение в виде равнобедренного треугольника (рисунок 10.9) Основные размеры: b = 9 см; h = 9 см; ρнар = R + ρвн = R - Определение положения нейтральной оси Как и в предыдущих примерах, брус имеет очень большую Поэтому нужно пользоваться точной формулой для радиуса кривизны нейтрального слоя: r= yo = R – r = 20 – 19,786 = 0,214 см.
Для сравнения определим yo по приближенной формуле (10.11). Площадь сечения: F = Главный центральный момент инерции Ix = yo ≈
Напряжения, связанные с изгибающим моментом: а) в наружных волокнах: yнар = (σM)нар =
Рисунок 10.9 б) во внутренних волокнах: yвн = - (σM) вн = Напряжения, связанные с продольной силой σN = Суммарные напряжения в наружных волокнах σнар = - M∙0.0276 + Суммарные напряжения во внутренних волокнах σвн = M∙0.0189 +
Результаты вычислений для трех сечений приведены в таблице.
Таблица 10.5
В данном случае опасным является сечение «С»участка ВС. Эпюра нормальных напряжений для этого сечения приведена на рисунке 10.9 справа. t Для сравнения вычислим напряжения в крайних волокнах соответствующего прямого бруса (эпюра показана штриховой прямой). (σМпр)нар = - (σМпр)вн = 10.3.4. Сечение в виде равнобедренной трапеции (рисунок 10.10) Основные размеры: bнар = 6 см; bвн = 10 см; h = 6 см. Расстояние от большего основания до центра тяжести: a = ρнар = R + (h - a) = 20 + (6 - 2,75) = 23,25 см; ρвн = R - a = 20 – 2,75 = 17,25 см. |
|
 + yо =
+ yо =  + 0,318 = 5,318 см;
+ 0,318 = 5,318 см; ∙
∙  =
=  ∙
∙  = - M∙0,00850 (кгс/см2);
= - M∙0,00850 (кгс/см2); =
=  = M∙0.01246 (кгс/см2).
= M∙0.01246 (кгс/см2). =
=  (кгс/см2).
(кгс/см2).










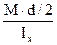 = ±
= ±  = ± 81,1 кгс/см2.
= ± 81,1 кгс/см2. =
=  =
=  = 19,576 см,
= 19,576 см, =
= 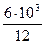 = 500 см4,
= 500 см4, =
=  = 0,417 см.
= 0,417 см. + yo =
+ yo =  ∙
∙  = - M∙0.00853 (кгс/см2);
= - M∙0.00853 (кгс/см2); ∙
∙  = M∙0.0120 (кгс/см2).
= M∙0.0120 (кгс/см2).










 (кгс/см2).
(кгс/см2). = ±
= ±  = ± 68,1 кгс/см2.
= ± 68,1 кгс/см2.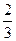 ∙h = 20 +
∙h = 20 +  ∙h = 20 -
∙h = 20 -  =
= 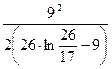 = 19, 786 см,
= 19, 786 см, =
=  = 40,5 см2.
= 40,5 см2. =
=  = 182,2 см4,
= 182,2 см4, = 0,225 см.
= 0,225 см. ∙h + yо =
∙h + yо = 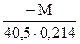 ∙
∙ 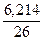 = - M∙0,0276 (кгс/см2);
= - M∙0,0276 (кгс/см2);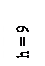










 = -
= -  = -2,786 см;
= -2,786 см; =
=  = M∙0,0189 (кгс/см2);
= M∙0,0189 (кгс/см2); (кгс/см2).
(кгс/см2). = -
= -  = - 262 кгс/см2,
= - 262 кгс/см2,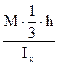 =
=  = 131 кгс/см2.
= 131 кгс/см2.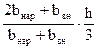 =
=  = 2,75 см;
= 2,75 см;