|
|
ТЕМА 2: АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ОРЛОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭКОНОМИКИ И ТОРГОВЛИ
Студента (ки) факультета экономики и управления
группы____________
ФИО______________________________
ОРЕЛ - 2016 ТЕМА 1: СВОДКА И ГРУППИРОВКА СТАТИСТИЧЕСКИХ ДАННЫХ Задача 1. Известны следующие данные о результатах сдачи абитуриентами вступительных экзаменов в баллах: 18, 17, 18, 16, 16, 12, 16, 14, 20, 15, 18, 19, 17, 20, 14, 12, 19, 18, 14, 15, 20, 19, 17, 16, 17, 18, 19, 20. Построить: 1) ранжированный ряд 2) ряд распределения абитуриентов по результатам сдачи ими вступительных экзаменов, выделив 4 группы абитуриентов с равными интервалами 3) ряд, делящий абитуриентов на поступивших в вуз, учитывая, что проходной балл – 15.
Решение: 1) Ранжированный ряд – это распределение единиц совокупности по возрастанию или убыванию.
2) Построим групповую таблицу, разбив абитуриентов на 4 группы:
3) Не поступившие – Поступившие – Задача 2. Имеются следующие данные о численности рабочих мест и товарообороте в среднем на одного продавца по 30 магазинам.
Построить: 1) групповую таблицу, разбив все магазины на несколько групп по числу рабочих мест; 2) комбинационную таблицу, дополнительно разбив сказуемое на несколько групп по величине товарооборота
Решение: 1) Для определения числа групп используется формула Стерджесса n = 1 + 3,322 lg N = Определим величину интервала:
Построим групповую таблицу, разбив все магазины по числу рабочих мест.
2) Построим комбинационную таблицу, дополнительно разбив сказуемое на несколько групп по величине товарооборота.
При построении комбинаций таблицы дополнительное число групп сказуемого должно быть меньше числа групп предшествующей группировки.
Пусть n = 4, тогда
Задача 3: Имеются основные показатели деятельности коммерческих банков одного из регионов на 01.01.11 г. (цифры условные) (тыс. руб.)
В качестве группировочного признака следует взять уставный капитал. Образуйте четыре группы банков с равными интервалами. Осуществите типологическую, структурную и аналитическую группировку. Решение: Величину интервала определим по формуле
Обозначим границы групп: - 1-я группа; - 2-я группа; - 3-я группа; -4-я группа. После того как определен группировочный признак - уставный капитал, задано число групп - 4 и образованы сами группы, необходимо отобрать показатели, которые характеризуют группы, и определить их величины по каждой группе. Показатели, характеризующие банки, разносятся по указанным группам, и подсчитываются итоги по группам. Результаты группировки заносятся в таблицу, и определяются общие итоги по совокупности единиц наблюдения по каждому показателю (табл. 2). Таблица 2. Группировка малых и средних коммерческих банков одного из регионов по величине уставного капитала на 01.01.11 г.
Структурная группировка коммерческих банков представлена в табл. 3.
Таблица 3. Группировка малых и средних коммерческих банков одного из регионов по величине уставного капитала на 01.01.11 г.
Из табл. 3 видно, что в основном преобладают ……………………… на долю которых приходится ……….% всего капитала. Более конкретный анализ взаимосвязи показателей можно сделать на основе аналитической группировки (табл. 4). Таблица 4. Группировка малых и средних коммерческих банков одного из регионов по величине уставного капитала на 01.01.11 г.
Величины капитала и работающих активов прямо взаимозависимы, и чем крупнее банк, тем эффективнее управление работающими активами. Задача 4: Имеются следующие данные о распределении коммерческих банков по объявленному уставному фонду:
С целью сравнения осуществите вторичную группировку коммерческих банков, для чего выделите следующие группы банков по объявленному уставному фонду: до 100, 100-500,500-100, 1000-5000, 5000-10000, свыше 10000. Сделайте соответствующие выводы. Решение: Вторичная группировка коммерческих банков по объявленному уставному фонду: (группировка единая)
ТЕМА 2: АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ Задача 1. В отчётном периоде поставка молочной продукции в торговую сеть характеризуется следующими данными:
Определите общий объём поставки молочной продукции торговой сети города в отчётном периоде, если существуют следующие коэффициенты пересчёта молочной продукции: молоко 3,2 % - 1; молоко 6% - 6; кефир – 1; ряженка – 2; сметана – 8,5; творог – 6,5.
Решение: С учётом представленных коэффициентов, общий объём поставок составит: Q =
Задача 2. Имеются следующие данные о производстве продукции промышленными предприятиями города в отчётном периоде:
Определите относительные величины выполнения плана. Решение: % выполн = % выполн1= % выполн2 = % выполн3 = % итого =
Задача 3. Прирост выпуска продукции отрасли по плану в отчётном году должен составить 7,5%. Фактически рост выпуска продукции в базисном году составил 109,5%. Определите относительную величину выполнения плана отраслью по выпуску продукции. Решение:
Задача 4. По плану отчетного года уровень годовой производительности труда работников должен возрасти по сравнению с прошлым годом на 3%. План по уровню производительности труда перевыполнен на 2%. Определите фактический и плановый уровень производительности труда, если известно, что в прошлом году уровень составлял 170 тыс. руб. Решение: Задача 5. По данным фирмы имеются следующие данные, в млн. руб.
Определите в целом по фирме: 1) размер планового задания по росту объёма реализованной продукции в отчётном году; 2) процент выполнения плана; 3) показатель динамики реализованной продукции. Решение: 1. ПЗ =. ОППЗ =
ОППЗ = 2. ОПВП =
ОПВП =
3. ОПД = Таким образом, фирма в целом
Задача 6. Имеются следующие данные о составе посевных площадей в агрофирмах области:
Определите относительные величины структуры.
Решение:
d1А= d1Б=
d2A= d2Б=
d3А= d3Б=
d4A= d4Б=
Задача 7. Имеются следующие данные о численности мужчин и женщин в области, тыс. чел.
Определите относительные величины координации (база – 1000 чел.) 1) для всего населения 2) в возрасте от 0 до 44 3) от 45 и старше Решение: 1) 2) 3) Задача 8. Производство промышленной продукции отдельными предприятиями характеризуется следующими данными:
Определите относительные величины сравнения. Решение:
Задача 9.Имеются данные о розничном товарообороте области за 2010 г., млрд. руб.: Розничный товарооборот — всего........................................14 403,3 по формам собственности: государственная ..............................................................1 445,7 негосударственная ........................................................12 957,6 в том числе частная...............................................10 723,1 Определите показатели структуры розничного товарооборота по формам собственности и показатели координации. Решение: Задача 10. Среднегодовая численность населения области в 2010 г. была 3540,7 тыс. человек. Из них занято в экономике 1926,2 тыс. чел. (в 2009 г. было занято 1957,1 тыс. чел. при общей численности населения 3418,1 тыс. чел.), безработные составили 55,4 тыс. чел. Среди безработных лица с высшим образованием – 3 тыс. чел., молодежь в возрасте от 16 до 29 лет – 7,8 тыс. чел., женщины – 38,4 тыс. чел. Определите относительные величины динамики, структуры, координации и интенсивности. Сделайте выводы. Решение: 1.ОПД = ОПД =
Т.о., за год численность населения.
2.ОПС = ОПСвыс = ОПСмол = ОПСж = Таким образом,
3.ОПК = часть 1/ часть 2 ОПК = Т.е., ОПИ = ТЕМА 3: СРЕДНИЕ ВЕЛИЧИНЫ. Задача 1.Заработная плата за неделю у 5-ти рабочих одного цеха составила 6500 руб., 4955 руб., 5323 руб., 5630 руб., 6150 руб. Определите средний уровень заработной платы рабочих Решение:
Задача 2.Имеются следующие данные о показателях работы предприятий отрасли за отчетный период:
Определите средние уровни каждого показателя по предприятиям отрасли. Решение:
Задача 3: Предприятием были выделены одинаковые денежные суммы на приобретение акций 2-х видов, при этом цена вида акций А - 1000 руб., а вида В - 1800 руб. Рассчитайте среднюю цену акции. Решение: Так как, в исходных данных совокупные показатели денежной суммы не известны, но сказано, что они одинаковы, а известны только индивидуальные значения признака, то для расчета воспользуемся средней гармонической простой:
Задача 4: Имеются следующие данные о коэффициентах роста среднедушевых доходов населения:
Определите средний коэффициент роста доходов населения. Решение: Так как, в исходных данных представлены относительные величины в виде перечня показателей, то воспользуемся формулой средней геометрической простой:
Задача 5: Имеются следующие данные по величине товарных запасов, тыс. руб.: На 01.01.2011 – 53123,6; На 01.04.2011 – 54165,7; На 01.07.2011 – 52173,8; На 01.10.2011 – 55630,2; На 01.01.2012 – 60886,3. Задание:определите среднюю величину товарных запасов. Решение:Так как исходные данные представлены на определённые даты, то используется формула средней хронологической.
Задача 6. Имеются данные об опыте работы предпринимателей:
Определите средний стаж предпринимателей по каждой сфере деятельности. Решение:
Задача 7.Имеются следующие данные
Задание: определите следующую выработку одного рабочего Решение:Так как данные представлены в виде произведения вариант на соответствующие частоты, то используется формула средней гармонической взвешенной:
Задача 8: Продажа подержанных автомобилей на товарной бирже города характеризуется следующими данными:
Определите среднюю цену одного авто в феврале и марте, а так же ее абсолютное и относительное изменение. Решение: 1. 2. 3. ОПД = Таким образом, за месяц на товарной бирже средняя цена одного автомобиля …………………….. Задача 9: Распределение пенсионеров города по размеру назначенных пенсий с учетом компенсационных выплат на начало года характеризуется данными:
Определите средний размер пенсии, моду и медиану. Решение: 1. Так как, исходными данными являются интервальные величины, то для перевода их в дискретные необходимо определить середины интервалов, ((нижняя граница интервала + верхняя граница)/ 2). Для определения середины интервала в открытом интервале к середине интервала предыдущего значения прибавляется величина интервала, (применяется только для рядов с равными интервалами).
2. Конкретное значение моды для интервального ряда определяется формулой:
где
Мо= 3. Формула медианы в интервальном ряду распределения будет иметь следующий вид:
где
Найдем медианный доход.
Ме =.
Вывод:
Задача 10: По данным исследований получены следующие данные по среднедушевому доходу в месяц, руб.:
Определите среднемесячный доход домохозяйств, моду, медиану. Решение: Для преобразования интервального ряда в дискретный, построим вспомогательную таблицу.
Мо=
Ме =. Задача 12.Имеются данные о распределении естественной убыли в 200 партиях товара.
Задание: определите средней % естественной убыли, моду, медиану. ТЕМА 4: РЯДЫ ДИНАМИКИ Задача 1.Имеются следующие данные о выпуске книг и брошюр, журналов и газет РФ (тыс. печатных единиц)
Задание:определите вид ряда динамики и его средний уровень. Решение: представленный ряд динамики является интервальным, поэтому его средний уровень рассчитывается по формуле средней арифметической простой:
Задача 2.Списочная численность работников фирмы в 2008 году оставила: на 1 января – 530 чел., на 1 марта – 570 чел., на1 июня – 520 чел., на 1 сентября – 430 чел., на 1 января следующего года – 550 чел. Задание:определите вид ряда динамики и его средний уровень. Решение:представленный ряд динамики является моментным, поэтому его средний уровень рассчитывается по формуле средней хронологической:
Задача 3: Имеются данные об объеме реализации продукции фирмы «Паллада», в которую до 2005 года входило 10 предприятий, а с 2006 года – 12.
Необходимо получить единый сопоставимый объём реализации путем смыкания рядов. Задача 4: Объем реализации организаций розничной торговли в одном из регионов в 2003 –2010 гг. характеризуется следующими данными, млн. руб.
Для анализа ряда динамики определите: 1) цепные и базисные: а) абсолютные приросты; б) темпы роста; в) темпы прироста; 2) для каждого года абсолютное значение 1 % прироста; 3) в целом за весь период среднегодовой абсолютный прирост и среднегодовой темп прироста. Результаты оформите в виде таблицы, сделайте выводы. Решение: 1) проанализируем полученный ряд динамики, используя следующие показатели: 12 |
|






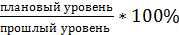

 =
=  %
%
 .гарм. =
.гарм. =  =
= =
= =
=
 =
= =
=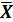 =
= 
 - нижняя граница модального интервала;
- нижняя граница модального интервала; - величина модального интервала;
- величина модального интервала; - частота, соответствующая модальному интервалу;
- частота, соответствующая модальному интервалу; - частота, предшествующая модальному интервалу;
- частота, предшествующая модальному интервалу; - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
 - нижняя граница медианного интервала;
- нижняя граница медианного интервала; - величина медианного интервала;
- величина медианного интервала; - полусумма частот ряда;
- полусумма частот ряда; - сумма накопленных частот, предшествующих медианному интервалу;
- сумма накопленных частот, предшествующих медианному интервалу; - частота медианного интервала.
- частота медианного интервала.

 .
.