Построение профиля по заданному направлению

На карте наносится профильная линия (линия СD на рис. 1.29), по которой требуется составить профиль местности. При составлении профиля выписывают расстояния между характерными точками и их отметки (рис. 1.30). Характерные точки находятся в местах пересечения профильной линии горизонталями (точки 1, 2, 4, 5 ... на рис. 1.29), водораздельными и водосливными линиями (точки 3, 13 – там, где уклон меняет знак).

Рис. 1.30. Построение профиля местности

Расстояния между точками определяют с округлением до точности масштаба (если М , то 0,1 мм – 1,0 м), отметки – до 0,1h_c.

Определение границы водосборной площади

Под водосборной площадью понимается та часть земной поверхности, с которой вода стекает к данному сечению водотока. Границы водосборной площади определятся водо-раздельными линиями. Пусть, например, в определенной точке водотока намечен створ водо-пропускного сооружения (рис. 1.31). От точек a и b граница водосборной площади пойдет перпендикулярно к ближайшим горизонталям и далее по водо-раздельным линиям.

Рис. 1.31. Схема построения
границы площади водосбора

Практическая часть

1. Вблизи вершины холма наметьте точку на карте. Представьте, что в этой точке находится источник воды, покажите направление ее стока.

2. Вычислите средний уклон линии в тысячных (в промиллях) с точки 1 на точку 2, если Н₁ = 117,5 м; H₂ = 112,3 м; d_1-2 = 187 м.

3. По графику заложений для углов наклона определите наибольший угол наклона по заданной линии квадрата километровой сетки.

4. Вычислите превышение с точки 1 на точку 2, если уклон линии
i_1-2 = – 0,028 и d_1-2 = 332 м.

5. Вычислите угол наклона с точки 1 на точку 2, если h_1-2 = 5 м и
d_1-2 = 191 м.

6. Вычислите заложения горизонталей, соответствующие уклону 0,03 для следующих значений высоты сечения рельефа: h_с = 2,5 м; h_c = 1,0 м;
h_с = 2,0 м; h_с = 0,5 м.

7. Вычислите крутизну ската для заложения, равного 1 см, на карте масштаба 1:10 000 при h_с = 2,5 м и h_с = 5 м.

8. От заданного на учебной карте сечения водотока (ручья) проведите границу водосборной площади.

Задание 1. Проведение горизонталей по отметкам точек и построение продольного профиля.

Задание заключается в составлении топографического плана участка местности в масштабе 1:5000 и построении продольного профиля по заданному направлению. Исходные данные для составления плана представлены на рис. 1.32 и в табл. 1.2.

Рис. 1.32. Схема расположения характерных точек местности

В верхней половине листа формата А4, на котором выполняется задание, вычертите прямоугольник размером 100 ´ 140 мм с сеткой квадратов 20 ´ 20 мм. В квадраты сетки на глаз с рис. 1.32 перенесите точки и вместо их номеров из табл. 1.2 выпишите отметки, согласно варианту, указанному преподавателем.

Определите характерные точки и линии рельефа и с учетом их положения произведите линейную интерполяцию для определения положения горизонталей согласно заданной высоте сечения рельефа. Работы выполните в соответствии с указаниями раздела 8. Горизонтали проведите плавными линиями толщиной 0,1 мм. Каждую пятую горизонталь утолстите до 0,25 мм. Утолщаются горизонтали с отметками, кратными 5 м, при высоте сечения рельефа через 1 м и с отметками, кратными 10 м, при высоте сечения рельефа через 2 м. На замкнутых горизонталях, а также по линиям водоразделов и тальвегов укажите направления скатов с помощью берг-штрихов. Подпишите отметки горизонталей.

После вычерчивания горизонталей с чертежа уберите все вспомогательные линии, закрепите отметки точек и с рис. 1.32 перенесите контуры в виде точечного пунктира. Образовавшиеся участки заполнить следующими условными знаками: I – смешанный лес, II – кустарник, III – огород, IV – пашня.

Таблица 1.2

Таблица отметок точек местности для выполнения задания 1

Окончание табл. 1.2

В нижней части листа составьте продольный профиль местности по направлению, заданному преподавателем. Горизонтальный масштаб такой же, как и для плана 1:5000. Вертикальный масштаб выберите в зависимости от перепада высот точек профиля – 1:100 или 1:200. При составлении профиля руководствуйтесь данными п. 8.4. Образец оформления задания 1 представлен на рис. 1.33.

	Задание № 1	Построение горизонталей и продольного профиля
Выполнил				ИСФ	Группа
Проверил

Рис. 1.33. Образец оформления задания 1

1.9. Определение планового положения точек земной поверхности

В соответствии с принятым в геодезии методом проекций задача изучения физической поверхности Земли распадается на две: определение положения горизонтальных проекций точек и определение их высот (отметок).

Принятые картографические проекции, системы координат различны, но во всех случаях положение точки в пространстве находят по трем координатам: высоте точки и двум координатам, определяющим местоположение проекции точки на уровенной поверхности (на поверхности сфероида).

Географические координаты

В системе географических координат местоположение проекции точки на сфероиде определяется двумя углами: широтой и долготой (рис. 1.34).

Рис. 1.34. Схема географических координат

Широтой точки j называют угол, образованный отвесной линией в данной точке и плоскостью экватора. Этот угол отсчитывается от плоскости экватора на север и на юг, изменяясь от 0 до 90°. Соответственно широта бывает северная (+) и южная (–).

Долготой точки l называют двугранный угол, заключенный между плоскостью начального (Гринвичского) меридиана и плоскостью меридиана, проходящего через данную точку. От начального меридиана долготу отсчитывают на восток и запад, от 0 до 180°. Соответственно долгота бывает восточная (+) и западная (–).

Для непосредственного определения географических координат точки на карте используют линии меридианов и параллелей. Меридиан – линия пересечения уровенной поверхности плоскостями, проходящими через ось вращения Земли, т.е. плоскостями долгот.

Параллель – линия пересечения уровенной поверхности плоскостями, перпендикулярными оси вращения Земли, т.е. плоскостями широт.

1.9.2. Зональная система плоских прямоугольных координат
(проекция Гаусса – Крюгера)

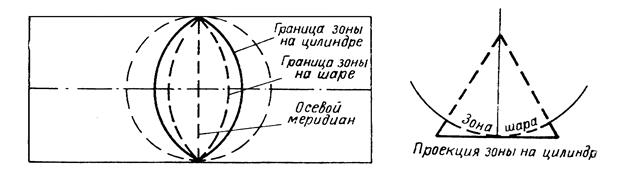
Зональная система плоских прямоугольных координат предложена Гауссом в 1828 г., удобные для практических расчетов формулы разработаны Крюгером к 1912 г., в СССР принята с 1928 г. Сущность проекции заключается в следующем. Поверхность земного сфероида делят меридианами на зоны в 6° по долготе, начиная от начального меридиана, и нумеруют по направлению к востоку (рис. 1.35), всего зон 60. Далее получают плоские изображения каждой зоны, для чего мысленно помещают сфероид внутрь цилиндра так, чтобы осевой меридиан зоны касался поверхности цилиндра (рис. 1.36). Из центра сфероида (рис. 1.37) зону проектируют на поверхность цилиндра – при этом углы сферы будут изображены без искажения, поэтому данную проекцию называют равноугольной, поперечно-цилиндрической. Изображение на поверхности цилиндра затем можно развернуть на плоскость.

В поперечно-цилиндрической проекции искажения будут в длинах линий: зоны на цилиндре получаются более широкими, чем на шаре. Не будет никаких искажений осевого меридиана – он касается поверхности цилиндра, но чем дальше расположены отрезки от осевого меридиана, тем больше искажений в длинах линий.

Рис. 1.35. Схема деления поверхности
земного сфероида на зоны

Ширина зоны на экваторе около 670 км, т.е. крайние точки зоны удалены от осевого меридиана примерно на 335 км. Искажения в длинах линий на экваторе достигают: при удалении от осевого меридиана на 100 км – , на 300 км – . Для широт территории РФ наибольшие искажения могут достигать примерно .

Наличие искажений в общем случае определяет возможное непостоянство масштаба в отдельных частях карты, и поэтому существуют понятия главного масштаба и частных масштабов. Главный – масштаб того глобуса, который изображают при составлении карты, частные масштабы относятся к различным частям карты.

Система географических координат удобна для изучения всей физической поверхности Земли или значительных ее участков, но неудобна для решения многих инженерных задач. Проекция Гаусса в географическом отношении не имеет практического значения, так как дает изображение земной поверхности с разрывами. Но ее ценность в том, что она в силу малых искажений сближает карту с планом и позволяет назначать систему плоских прямоугольных координат в каждой зоне, что удобно при решении инженерных задач.

В проекции Гаусса за начало координат в каждой зоне принимают точку пересечения осевого меридиана с линией экватора, которые образуют прямой угол. Они и есть в данном случае оси координат (рис. 1.38). Осевой меридиан служит осью абсцисс x, а линия экватора – осью ординат у. Положительным направлением абсцисс считается направление от экватора к северу, положительным направлением ординат – на восток. В математике применяется левая система координат (нумерация четвертей против движения часовой стрелки), в геодезии – правая система. Но так как наименования осей координат тоже противоположны, знаки координат точек, расположенных в одноименных четвертях, совпадают (см. рис. 1.38), что позволяет применять формулы тригонометрии без всяких изменений и в данной системе.

Математика	Геодезия
I x+ y+	I x+ y+
II x– y+	II x– y+
III x– y–	III x– y–
IV x+ y–	IV x+ y–

Рис. 1.38. Координатные оси в прямоугольной системе координат

Для территории РФ, расположенной в северном полушарии, абсциссы х везде положительны, а ординаты у могут быть и положительными, и отрицательными, например, для точки А (см. рис. 1.38) x_A = 700 км; y_A = – 300 км. Отрицательные ординаты затрудняют обработку геодезических материалов. Чтобы избежать этого, ординату осевого меридиана принимают не за 0, а за 500 км. Следовательно, к ординатам всех точек зоны прибавляется эта условная величина (500 км), и теперь у_А = – 300 + 500 = 200 км.

Дополнительно в записи ординаты точки указывают номер зоны в связи с тем, что во всех шестидесяти зонах системы координат одинаковые. Следовательно, значение координат точки необходимо дополнить номером зоны, в которой эта точка находится. Этот номер приписывается впереди ординаты, и если в нашем случае точка А (см. рис. 1.38) находится в третьей зоне, то запись ординаты будет у_А = 3200 км.

Таким образом, ординаты точек получают преобразования и соответственно называются преобразованными. Для определения местоположения точки в зоне следует, зная ее координаты, действовать в обратном порядке: убрать из записи ординаты номер зоны и вычесть 500 км.

Практическая часть

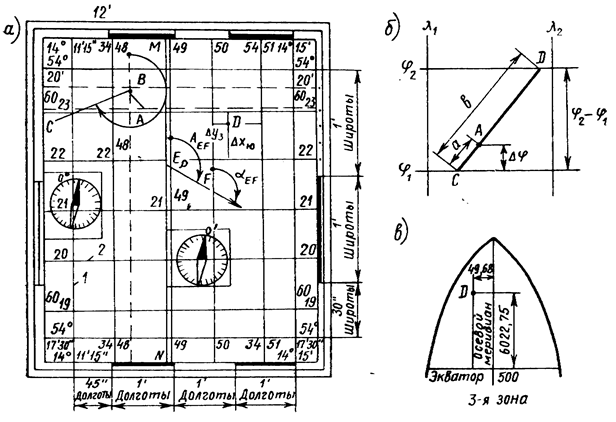
Освоение обозначений систем координат на учебной топографической карте масштаба 1:10 000 и определение координат точек

Географическая система координат. Лист карты окаймляют три рамки: внутренняя, минутная и внешняя. Внутренняя рамка имеет форму трапеции (что наглядно видно на картах более мелкого масштаба). Эта рамка образована отрезками меридианов и параллелей, непосредственно ограничивающих картографическое изображение. На выходах этих линий в углах рамки указаны соответствующие значения широты и долготы. Так, на рис. 1.39, а лист карты ограничен по долготе 14°11¢15² – 14°15¢00² и по широте 54°17¢30² – 54°20¢.

Минутная рамка с обозначением определенного интервала широт и долгот служит для более точного измерения географических координат точек на карте. Минутные и полуминутные интервалы отмечены утолщенными линиями, десятисекундные интервалы – точками. Соответственно на рисунке начало первых утолщенных линий определяет точку с долготой l = 14°12¢ и с широтой j = 54°18¢. Внешняя рамка имеет декоративное назначение.

Рис. 1.39. Схема определения географических и прямоугольных координат

Широта j_B и долгота l_B точки В, заданной на карте, определяется параллелью и меридианом, проходящим через эту точку. Для определения j_B и l_B без построения линий параллели и меридиана через данную точку следует соединить прямыми линиями одноименные концы минутных или десятисекундных интервалов, далее применить линейную интерполяцию, для чего положить линейку с миллиметровыми делениями так, чтобы отсчитать отрезки a и b (рис. 1.39, б). Тогда

.

На рис. 1.38, а для точки В j₁ = 54°19¢40²; j₂ = 54°19¢50²;
j_B = 54°19¢40² + 10² = 54°19¢48². Аналогично, проведя меридианы l₁и l₂ (рис. 1.39, б), определите долготу l_B. Для контроля j и l нужно вычислять дважды, при двух различных положениях линейки, т.е. при различных значениях отрезков а и b. Далее следует определить географические координаты двух точек. Вначале определите координаты точек на глаз, затем для одной из точек уточните координаты по приведенному выше способу (для соединения одноименных интервалов потребуется линейка длиной более 40 см).

Прямоугольная система координат Гаусса–Крюгера. В этой системе координаты на листе карты представлены сеткой квадратов (см. рис. 1.39, а). Размер квадрата должен быть кратным целому числу километров, поэтому сетка называется километровой (линии сетки 1, 2 на рис. 1.39, а).

Абсциссы х, за начало отсчета которых принимают линию экватора, подписаны у горизонтальных линий, при этом сотни километров приводятся не у всех линий. Например, абсцисса 6019 выписана полностью, у абсциссы 6020 приведена только цифра 20 («сокращенная абсцисса»). Система надписей у ординат аналогична, при этом ординаты точек указываются преобразованными.

При обозначении квадратов километровой сетки применяются сокращенные координаты (квадраты 22/48; 21/49 и т.д. на рис. 1.39, а).

Для получения значений координат точки D измеряют отрезки Dx_ю и Dу_зот южной и западной сторон квадрата километровой сетки. Для контроля проводят аналогичные измерения от северной и восточной сторон квадрата: Dx_с и Dу_в.

Сторона километровой сетки равна 1000 м, и потому разности
f_x = (Dx_ю + Dx_с) – 1000 и f_y = (Dу_з + Dу_в) – 1000 представляют собой погрешности в определении координат. Точность измерения считается достаточной, если f_x и f_y [м] не превосходят числа тысяч в знаменателе численного масштаба карты. В этом случае f_x и f_y распределяются с обратным знаком, пропорционально измеренным величинам Dx и Dу.

Пусть для точки D (квадрат 22/50) получено: x_D = 6022,75 км и у_D = = 3450,32 км. Действительное значение ординаты будет y_{Dдейств} = 450,32 – –500 = – 49,68 км[1]. Точка D расположена в 3-й зоне, находится западнее осевого меридиана (рис. 1.39, в).

Упражнения.Найдите координаты двух точек при условии первоначального определения на глаз. Затем для одной точки уточните координаты измерениями, определите по приведенному ранее способу погрешности и распределите их. Для этой же точки вычислите действительное значение ординаты, покажите ее местоположение на схеме зоны.

1.10. Ориентирование линий, планов и карт

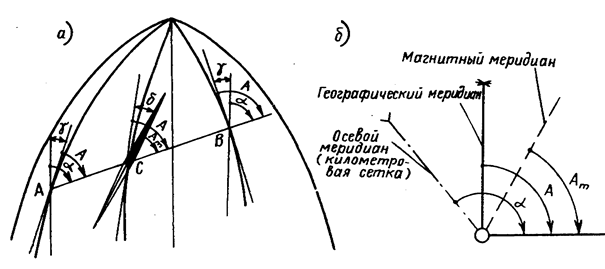
Для ориентирования карты достаточно ориентировать линию, принадлежащую данной карте.

Для того чтобы ориентировать линию, надо знать угол ориентирования, т.е. тот угол, который данная линия составляет с направлением, принятым за начальное.

В географической системе за начальное направление принято северное направление географического меридиана (рис. 1.40, 1.41) и углами ориентирования являются географический азимут A и географический румб r_г.

Географический азимут – угол, отсчитываемый от северного направления географического меридиана по ходу часовой стрелки до ориентируемой линии. Изменяется от 0 до 360°.

Но географические меридианы в разных точках сфероида не параллельны между собой, поэтому азимут одной и той же линии (см. рис. 1.40, линия 1–2) в различных ее точках будет различен (азимут A_(A)в точке А не равен азимуту A_(B) в точке В. Это различие определяет угол g, который называется сближением меридианов: g = А_(В) – А_(А)(см. рис. 1.40, 1.41).

В геодезии пользуются терминами: прямое направление линии и обратное. Так, если исходное направление линии – направление АВ
(см. рис. 1.41), то обратное направление – направление ВА. Соответственно азимут линии АВ будет прямым, линии ВА – обратным (т.е. А_(А), А_(В) – азимуты прямые, А_(В)обр – азимут обратный). Зная азимут прямой в точке А_(А)и сближение меридианов g_(В),можно вычислить азимут обратный в точке В. В данном случае А_(В)обр = А_(А) + 180° + g_(В).

Расчет показал, что для средних широт при расстояниях между точками менее 0,5 км сближение меридианов менее 30². В строительной практике такая погрешность (30²) в определении направлений считается допустимой, и тогда при l < 0,5 км в общем случае А_обр = А_пр±180°.

На рис. 1.39,а показан географический азимут для линии ВС (пунктирная линия – направление географического меридиана в точке В).

Географический румб – острый угол между ориентируемой линией и ближайшим направлением географического меридиана (северным или южным). Румб может иметь значения от 0 до 90°. Связь румбов и азимутов показана на рис. 1.42. Числовые значения румба необходимо сопровождать названием четверти, в которой находится линия. Например, для линии MN₁румб составит r = СВ: 56°15¢, для линии MN₃ r = ЮЗ: 31°26¢ и т.д.

Обратные румбы отличаются от прямых названием, их угловая величина не меняется. Так, если прямой румб r = CВ: 50°15¢, то обратный румб r = ЮЗ: 50° 15¢.

В системе плоских прямоугольных координат за начальное направление принято северное направление осевого меридиана (рис. 1.43), и углами ориентирования являются дирекционный угол a и дирекционный румб r. Соответственно в пределах зоны сближение меридианов g есть угол, образованный направлением осевого меридиана и направлением географического меридиана данной точки.

Дирекционный угол – угол, отсчитываемый от северного направления осевого меридиана или линии, ему параллельной, по ходу часовой стрелки до ориентируемой линии. Изменяется от 0 до 360°.

Дирекционный угол в разных точках прямой – величина постоянная, и соответственно обратный дирекционный угол равен: a_обр = a_пр + 180°.

Зная географический азимут, можно вычислить дирекционный угол, и наоборот. Если считать для точек, расположенных восточнее осевого меридиана, сближение g со знаком плюс (см. рис. 1.43), а западнее – со знаком минус, то во всех случаях А = a+ g.

На топографических картах дается значение g для средней точки листа карты. При решении задач следует иметь в виду, что для карт
М и М сближение меридианов изменяется на 30¢.

Дирекционный румб – острый угол между ориентируемой линией и ближайшим направлением осевого меридиана или линии, ему параллельной изменяется от 0 до 90°. Связь между румбами и дирекционными углами такая же, как и в географической системе.

На топографической карте представлены географическая система и система плоских прямоугольных координат. Соответственно направления линий характеризуются географическими азимутами или дирекционными углами.

В тех случаях, когда необходимо ориентировать карту на местности, или линию местности определенного направления отобразить на карте или плане, или решить другие аналогичные задачи, т.е. «перейти от карты к местности», и наоборот, во многих случаях ориентируются относительно магнитного меридиана, направление которого определяется магнитной стрелкой.

При ориентировании относительно магнитного меридиана за начальное направление принято северное направление магнитного меридиана (рис. 1.44) и углами ориентирования являются магнитный азимут А_т и магнитный румб r_m.

Рис. 1.44. Схема определения
магнитных азимутов

Магнитный азимут – угол, отсчитываемый от северного направления магнитного меридиана, по ходу часовой стрелки до ориентируемой линии.

Магнитный меридиан, как правило, не совпадает с геогра-фическим. Угол, образованный этими меридианами, называется магнитным склонением d (см. рис. 1.44). Приписывая восточному склонению знак плюс, а западному минус, во всех случаях получаем:

А = А_т + d.

Магнитное склонение – величина не постоянная, известны его суточные, годовые и вековые изменения. В частности, суточное изменение в средней полосе территории РФ достигает 15¢ и больше, следовательно, ориентирование линий относительно магнитного меридиана возможно в тех случаях, когда не требуется высокой точности. Есть районы, где вообще нельзя пользоваться показаниями магнитной стрелки. Уточненную величину магнитного склонения можно узнать на метеостанциях и по специальным картам, его среднее значение приводится на топографических картах.

Магнитный румб – острый угол между ориентируемой линией и ближайшим направлением магнитного меридиана. Связь между магнитными румбами и азимутами такая же, как и в географической системе.

Схема связи дирекционных углов и азимутов приведена на
рис. 1.45, а,б. Их аналитические зависимости: А = a+ g; А = А_т + d.

Рис. 1.45. Связь дирекционных углов и азимутов

Ориентирование карты осуществляется при помощи двух приемов (см. рис. 1.39, а).

1. Приложив буссоль (компас) к боковой линии рамки карты (т.е. к линии географического меридиана), следует поворачивать карту до тех пор, пока по северному концу магнитной стрелки не будет получен отсчет, равный магнитному склонению d.

2. Приложив буссоль к линии километровой сетки (т. е. к направлению осевого меридиана), поворачивают карту до получения отсчета, равного поправке П(включающей d и g): П = d – g.

Практическая часть

Определение географического азимута. В пределах квадрата километровой сетки проведите в средней части карты линию EF (см. рис. 1.39, а). Для определения азимута необходимо иметь на карте направление географического меридиана. Как и ранее, построение меридиана, ближайшего к точке E, производится соединением одинаковых долгот южной и северной рамок карты (линия MN на рис. 1.39, а). Продлив линию EF до пересечения с линией MN (в точке E), измерьте геодезическим транспортиром географический азимут линии. По измеренному азимуту вычислите румб линии и запишите его в принятой форме. Вычислите обратный азимут и обратный румб той же линии.

Определение дирекционного угла. Для определения дирекционного угла той же линии EF следует продлить ее до пересечения с вертикальной линией километровой сетки, измерить по транспортиру угол a. Вычислите сближение меридианов по зависимости g = А – a, сопоставьте с величиной сближения, приведенного на схеме, расположенной за южной рамкой карты. Проанализируйте полученные результаты (по величине и знаку).

Ориентирование карты по магнитному меридиану. Для такого ориентирования применяется буссоль. Основные поверки буссоли следующие.

1. Магнитная стрелка должна быть хорошо намагничена. Освободив стрелку и дав ей успокоиться, делают отсчет. Затем к стрелке буссоли подносят железный предмет (ключ, отвертку и т. п.) и отводят стрелку на 10–20°. Быстрым движением убирают предмет в сторону, стрелке дают успокоиться и делают второй отсчет. Если отсчеты совпадают, а стрелка останавливается после небольших колебаний, то условие выполнено.

2. Магнитная стрелка должна быть уравновешена. Буссоль устанавливают в горизонтальное положение. Если концы стрелки находятся на одинаковых расстояниях от верхней плоскости кольца буссоли, то условие выполнено. Убедившись в исправности буссоли, ориентируйте карту обоими способами.

Измерение дирекционного угла и вычисление географического и магнитного азимута. Для прямолинейного отрезка автомобильной или железной дороги измерьте по транспортиру дирекционный угол. Возьмите со схемы, приведенной на карте, величины сближения и склонения, вычислите географический и магнитный азимуты. По полученным данным вычислите румбы, запишите их в принятой форме.