|
|
Причины возникновения погрешностей.Введение. Измерение физических величин и получение их числовых значений являются непосредственной задачей большинства физических экспериментов. При измерениях значение физической величины выражается в виде числа, которое указывает, во сколько раз измеренная величина больше (или меньше) другой величины, например, времени, пути, скорости и т. д. Физика устанавливает связь между такими величинами и выражает ее в виде формул, которые показывают, как числовые значения одних величин могут быть найдены по числовым значениям других. Получение надежных числовых значений не является простой задачей из-за погрешностей, неизбежно возникающих при измерениях. Мы рассмотрим эти погрешности, а также методы, применяемые при обработке результатов измерений. Владение этими методами нужно для того, чтобы научиться получать из совокупности измерений наиболее близкие к истине результаты, вовремя заметить несоответствия и ошибки, разумно организовать сами измерения и правильно оценить точности полученных значений. Измерения подразделяются на прямые и косвенные. В зависимости от вида измерений существуют различные методы оценки их точности. В свою очередь погрешности, допускаемые в процессе эксперимента, разделяются на систематические, случайные и грубые ошибки (промахи). Прямые измерения производятся с помощью приборов, которые измеряют непосредственно саму исследуемую величину. Так, массу тела можно найти с помощью весов, длину измерить линейкой, а время – секундомером. К косвенным относятся измерения таких физических величин, для нахождения которых необходимо использовать связь в виде формулы с другими, непосредственно измеряемыми величинами, например, нахождение объема тела по его линейным размерам, нахождение плотности тела по измеренным массе и объему, расчет сопротивления проводника по показаниям вольтметра и амперметра. Причины возникновения погрешностей. Из-за действия множества искажающих факторов результат каждого отдельного измерения физической величины не совпадает с ее истинным значением. Разность между результатом измерения и истинным значением измеряемой величины называется погрешностью измерений (ошибкой измерений). Различают три типа погрешностей измерений: грубые ошибки (промахи), систематические и случайные погрешности. Грубые ошибки, или промахи, обычно бывают связаны с неисправностью измерительной аппаратуры, либо с ошибкой экспериментатора в отсчете или записи показаний приборов, либо с резким изменением условий измерений. Результаты измерений, соответствующих грубым ошибкам, нужно отбрасывать и взамен проводить новые измерения. Методические погрешности обусловлены неадекватностью принимаемых моделей реальным объектам. Например, при измерении геометрических параметров вала или трубы их моделируют цилиндром. Диаметр цилиндра должен быть одинаков во всех сечениях и всех направлениях, образующие также должны иметь одинаковую длину. Однако в силу внутренних особенностей материала и несовершенства используемых технологий изготовления это правило обычно нарушено. Другая причина – несовершенство методов измерений. Если расстояние между двумя точками порядка 100 м измеряется посредством многократного наложения метровой линейки, то в результате измеряется длина некоторой ломаной линии. Погрешность может быть обусловлена также упрощением зависимостей, положенных в основу измерений. Например, ускорение свободного падения g можно определить, если измерить время t, в течение которого некоторое тело в свободном падении пройдет определенное расстояние h . При этом пользуются соотношением
которое справедливо, если на тело действует только сила тяжести. Реально на тело действует также сила сопротивления, которая в данном случае не учитывается. Инструментальные (приборные) погрешности обусловлены особенностями принципов и методов измерений, используемых в приборах, а также их схемным, конструктивным и технологическим несовершенством. Одна из причин такой погрешности – погрешность калибровки, возникающая в процессе перехода от эталона к реальному средству измерения. Приборные погрешности определяются при испытании средства измерения и указываются в технической документации. Уменьшение инструментальной погрешности достигается применением более совершенных и точных приборов. Однако полностью устранить приборную погрешность невозможно. Систематические погрешности сохраняют свою величину и знак во время эксперимента. Они могут быть связаны с ошибками приборов (неправильная шкала, неравномерно растягивающаяся пружина, неравномерный шаг микрометрического винта, неравные плечи весов) и с самой постановкой опыта, например, при взвешивании тела малой плотности без учета выталкивающей архимедовой силы, которая систематически занижает вес тела. Систематические погрешности опыта могут быть изучены и учтены путем внесения поправок в результаты измерений. Если систематическая погрешность опыта слишком велика, то обычно оказывается проще использовать новые, более точные приборы, чем исследовать погрешности старых. Оценку систематических погрешностей экспериментатор проводит, анализируя особенности методики, паспортную точность прибора и проводя контрольные опыты. В учебном практикуме учет систематических ошибок ограничивается, как правило, лишь случаем инструментальных погрешностей. Систематические погрешности стрелочных электроизмерительных приборов (амперметров, вольтметров, потенциометров и т. п.) определяется их классом точности, который выражает абсолютную погрешность прибора в процентах от максимального значения включенной шкалы. Пусть на шкале вольтметра с диапазоном показаний от 0 до 10 В в кружке стоит цифра 1. Эта цифра показывает, что класс точности вольтметра равен 1 и предел его допустимой погрешности равен 1% от максимального значения включенной шкалы, т. е. равен
где K – класс точности прибора, Aмакс – верхний предел измерений прибора (либо данного его диапазона). Кроме того, надо иметь в виду, что наносить деления на шкале принято с таким интервалом, чтобы величина абсолютной погрешности прибора не превышала половины цены деления шкалы. Класс точности стрелочных электроизмерительных приборов (как и полцены деления шкалы) определяет максимальную (предельную) абсолютную погрешность, величина которой не меняется вдоль всей шкалы. Относительная же погрешность при этом резко меняется, поэтому приборы обеспечивают лучшую точность при отклонении стрелки почти на всю шкалу. Отсюда следует рекомендация: выбирать прибор так, чтобы стрелка прибора при измерениях находилась во второй половине шкалы. Относительную погрешность прибора можно рассчитать по формуле:
В последнее время широко используются цифровые универсальные приборы, в том числе и электроизмерительные, отличающиеся высокой точностью и многоцелевым назначением. В отличие от стрелочных приборов систематические погрешности цифровых электроизмерительных приборов оцениваются по формулам, приводимым в инструкциях по эксплуатации. Если класс точности прибора не указан и в паспорте прибора нет данных относительно его инструментальной погрешности, то обычно считают, что эта погрешность равна половине цены наименьшего деления шкалы прибора. В случае прибора, стрелка которого перемещается не равномерно, а «скачками» (например, у ручного секундомера), приборную погрешность считают равной цене деления шкалы. Случайные погрешности измерений меняют величину и знак от опыта к опыту. Многократно повторяя одни и те же измерения, можно заметить, что довольно часто их результаты не в точности равны друг другу, а «пляшут» вокруг некоторого среднего значения. Случайные погрешности могут быть связаны, например, с сухим трением (из-за которого стрелка прибора вместо того, чтобы останавливаться в правильном положении, «застревает» вблизи него), с люфтом в механических приспособлениях, с тряской, которую в городских условиях трудно исключить, с несовершенством объекта измерений (например, при измерении диаметра проволоки, которая из-за случайных причин, возникающих при изготовлении, имеет не вполне круглое сечение) или с особенностями самой измеряемой величины. Примером в последнем случае может быть число космических частиц, регистрируемых счетчиком за 1 минуту. Повторяя измерения, найдем, что в разных опытах получаются разные числа, хотя и не слишком отличающиеся друг от друга, колеблющиеся около некоторого среднего значения. Случайные погрешности эксперимента исследуются путем сравнения результатов, полученных при нескольких измерениях, проведенных в одинаковых условиях. Если при двух-трех измерениях, проведенных в одинаковых условиях, результаты совпали, то на этом следует остановиться. Если они расходятся, нужно попытаться понять причину расхождения и устранить ее. Если устранить причину не удается, следует произвести 10-12 измерений и, записав все результаты, обработать их в соответствии с полученной закономерностью разброса величин. Случайные погрешности устранить нельзя, но благодаря тому, что они подчиняются вероятностным закономерностям, всегда можно указать пределы, внутри которых с заданной вероятностью заключается истинное значение измеряемой величины. Задача определения случайных погрешностей была решена созданием теории, хорошо согласующейся с экспериментом. В основе этой теории лежит закон нормального распределения, включающий следующие закономерности: 1. При большом числе измерений ошибки одинаковой величины, но разного знака, встречаются одинаково часто. 2. Частота появления ошибок уменьшается с ростом величины ошибки. Иначе говоря, большие ошибки наблюдаются реже, чем малые. 3. Ошибки измерений могут принимать непрерывный ряд значений. Случайные погрешности изучают, опираясь на изложенные закономерности, и для понимания такого подхода требуется ввести понятие вероятности. Статистическая вероятность события определяется отношением числа n случаев его проявления к общему числу N всех возможных равновероятных случаев:
Надежностью результата измеренияфизической величины А называется вероятность Р того, что истинное значение А действительно лежит в интервале от Абсолютной погрешностью измерений называют разность между найденным на опыте и истинным значением физической величины. Обозначая абсолютную погрешность измерения величины А символом
Кроме абсолютной погрешности
Качество измерений обычно определяется именно относительной, а не абсолютной погрешностью. Одна и та же погрешность в 1 мм при измерении длины комнаты не играет роли, при измерении стола может быть существенна, а при определении диаметра болта совершенно недопустима. За наиболее достоверное значение непосредственно измеряемой величины А принимают среднее арифметическое <A> из всех n результатов ее измерений А1, А2, …, Аi, …, Аn:
Окончательный результат измерения величины А представляют в форме
При числе измерений n
Если необходимо повысить надежность результата, то значение
где t – положительный коэффициент, задаваемый распределением Стьюдента. Значения коэффициентов Стьюдента рассчитаны и приведены в таблицах. 12 |
|
 ,
, 0,1 В. Общая формула для расчета максимальной абсолютной погрешности имеет вид:
0,1 В. Общая формула для расчета максимальной абсолютной погрешности имеет вид: ,
, .
.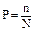
 до
до 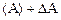
 , получим
, получим .
. часто бывает важно знать относительную погрешность
часто бывает важно знать относительную погрешность  измерений, которая равна отношению абсолютной погрешности к значению измеряемой величины:
измерений, которая равна отношению абсолютной погрешности к значению измеряемой величины: .
. .
. .
. 5 с надежностью Р
5 с надежностью Р  2/3 можно принять, что абсолютная погрешность
2/3 можно принять, что абсолютная погрешность  .
. ,
,