|
|
Обработка результатов при косвенных измерениях.В большинстве экспериментов интересующая нас величина непосредственно не измеряется. Вместо этого мы измеряем некоторые другие величины А, В, С, и т.д., а затем вычисляем величину Z , которая является известной функцией указанных первичных величин. Пусть каждая первичная величина измерена несколько раз, найдено ее среднее значение и погрешность измерения, и пусть измерения первичных величин независимы и поэтому их погрешности тоже независимы. Зная средние значения <А>, <В> и т.д., можно вычислить <Z> и оценить погрешность ΔZ через погрешности ΔА, ΔВ и т.д. Для определения результирующей погрешности ΔZ необходимо знать ΔZА , ΔZB,…, обусловленные отдельными прямыми измерениями. Здесь ΔZA определяет погрешность величины Z, обусловленную погрешностью в определении величины А при условии, что все остальные аргументы В, С и т.д. имеют значения в точности равные <В>, <C> и т.д. Ее можно вычислить по формуле
где ∂Z/∂А -частная производная, при вычислении которой все величины, кроме А, предполагаются постоянными. Результирующая погрешность определяется по формуле
Иногда бывает удобно находить сначала относительную погрешность δZ
где δZA -относительная погрешность величины Z, обусловленная погрешностью в определении величины А. Для ее определения используется соотношение
Таким образом, для определения относительной погрешности можно прологарифмировать функцию Z(A,B,...) и, взяв частные производные от lnZ по каждой из переменных, воспользоваться вышеприведенными соотношениями. Пусть для косвенных измерений физической величины А используется известная функциональная зависимость А от ряда других независимых величин B, C, D, E, F, …, Q, заданная в форме Среди переменных B, C, …, Q могут быть величины трех типов: 1) величины, определяемые путем прямых измерений (например, величины E, F, …, Q), которые после проведения этих измерений представляются в стандартной форме:
2) данные установки (например, величины B и C), т. е. характеристики экспериментальной установки, известные из предыдущих измерений; эти величины также должны быть заданы в аналогичной форме:
3) табличные величины (например, величина D) – величины, которые в данном опыте не измеряются, а берутся из таблиц. Табличная величина может быть константой (например, D=π). В этом случае ее нужно брать из таблиц с такой точностью, чтобы относительная погрешность D была значительно меньше относительных погрешностей всех остальных величин, входящих в функциональное выражение для искомой величины А. Если же D – заданная в табличной форме функция непосредственно измеряемой величины T, то ее также нужно представить в стандартной форме:
где <D> - табличное значение, соответствующее <T>; Наилучшим значением величины А при косвенном ее измерении будет
а стандартная погрешность А принимается равной
Окончательный результат также представляется в стандартной форме:
Формулы расчета погрешностей при косвенных измерениях в некоторых простейших случаях:
Графики. Графики строят при изучении функциональной зависимости одной величины от другой. Они являются одним из наиболее важных методов для анализа данных и представляют результаты в наиболее наглядной форме, выдавая максимум информации на минимальном пространстве. Построив график, мы сразу выявляем характерные особенности изучаемых зависимостей: области возрастания или убывания, максимумы и минимумы, скорость изменения функции, периодичность и т.д. Графики позволяют выявить область, где существует определенная зависимость между величинами, и на основании этого сделать вывод о характере физических процессов. При построении графиков нужно руководствоваться определенными правилами. 1. График выполняется на миллиметровой бумаге. Построение графика начинают с нанесения координатных осей, при этом аргумент - величина, значение которой задает сам экспериментатор, - откладывается по оси абсцисс, а функция - величина, определяемая из эксперимента, - по оси ординат.2. На координатные оси наносят масштаб, который выбирается в соответствии с интервалом изменения переменных независимо для каждой из них. Начало координат (точку 0,0) не обязательно помещать на графике. Это необходимо лишь в том случае, когда нужно подчеркнуть, что кривая проходит через точку 0,0. Во всех остальных случаях, особенно, когда значения переменных существенно отличаются от нуля, а интервал их изменения невелик, нулевое значение величины может остаться за пределами построенного графика. Выбирая масштаб, нужно стараться, чтобы график занимал всю отведенную для него площадь, а не ютился где-то в уголке. Ценность графика во многом зависит от удачного выбора масштаба. Проще всего, если единица измеренной величины (или 10; 100; 0,1 и т.д.) соответствует 1см на координатной оси. Можно выбрать масштаб, когда 1см соответствует 2 или 5 единицам. Других масштабов следует избегать, чтобы при нанесении точек на график не приходилось, например, делить 1см на 3 или 7 частей. Цифры не обязательно указывать против каждого деления масштаба, их число тоже диктуется соображениями удобства, В конце оси указывается откладываемая величина и ее размерность (I, А). Множитель 10n, определяющий порядок величины, лучше отнести к единице измерения, например, I,мА или I,10-3А. Часто при исследовании функциональных зависимостей применяют логарифмический масштаб. Когда интересующая нас зависимость имеет вид у=ах, то логарифмическую шкалу применяют только для одной координатной оси (оси у). При этом в зависимости от значения величины а можно пользоваться как десятичными, так и натуральными логарифмами. Удобство такого метода состоит в том, что при таком подходе мы получаем линейную зависимость величины lnу от х. Если же исследуемая зависимость имеет вид у=ха, то удобнее применить логарифмическую шкалу для обеих осей, ибо в этом случае указанная зависимость представляется прямой линией и величина показателя степени а может быть определена по тангенсу угла, образованного этой линией с координатными осями (угловой коэффициент прямой).
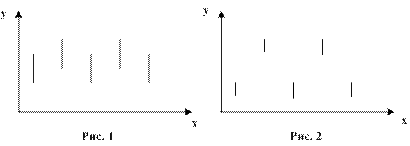
4. Погрешности указывают для одной или обеих измеряемых величин в виде отрезков длиной в доверительный интервал, в центре которых расположены экспериментальные точки, или в виде прямоугольника, стороны которого равны доверительным интервалам. Это особенно необходимо, когда от величины погрешности зависит интерпретация результатов эксперимента. Например, на рис.1,2 приведены результаты различных экспериментов по изучению зависимости величины у от величины х. В случае рис.1 эксперимент не выявляет зависимости величины у от х, а на рис.2 такая зависимость очевидна. 12 |
|
 ,
,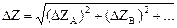
 ,
,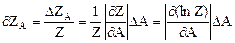 .
. .
.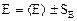 ,
, 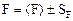 , …,
, …,  ;
;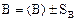 и
и  ;
;
 ,
,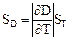 , а
, а 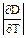 определяется с помощью таблицы.
определяется с помощью таблицы.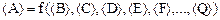 ,
,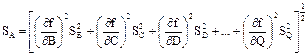
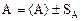 .
.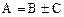

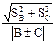
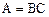
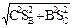

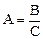
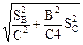
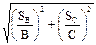

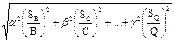
 3. После построения координатных осей приступают к нанесению на график экспериментальных данных. (При этом отмечать на координатных осях значения измеренных на опыте величин недопустимо). Экспериментальные точки должны быть четко видны на графике. Через экспериментальные точки проводят "наилучшую" плавную кривую. Кривая не должна заслонять экспериментальные точки, поскольку именно они являются результатом опыта, а кривая - лишь толкование результата. Если на графике имеется теоретическая кривая, то кривую через экспериментальные точки лучше не проводить. При построении теоретической кривой точки, по которым она строится, ставят без нажима, чтобы они не были видны после проведения линии.
3. После построения координатных осей приступают к нанесению на график экспериментальных данных. (При этом отмечать на координатных осях значения измеренных на опыте величин недопустимо). Экспериментальные точки должны быть четко видны на графике. Через экспериментальные точки проводят "наилучшую" плавную кривую. Кривая не должна заслонять экспериментальные точки, поскольку именно они являются результатом опыта, а кривая - лишь толкование результата. Если на графике имеется теоретическая кривая, то кривую через экспериментальные точки лучше не проводить. При построении теоретической кривой точки, по которым она строится, ставят без нажима, чтобы они не были видны после проведения линии.