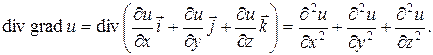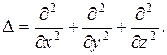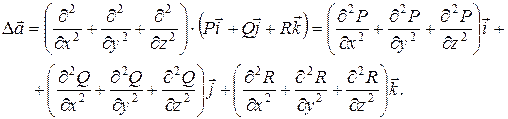|
|
Градиент, дивергенция, роторБрянск 2011
Составители: Баранова И.М., зав. кафедрой математики, Алексеева Г.Д., доцент кафедры математики, Часова Н.А., доцент кафедры математики, Муравьев А.Н., доцент кафедры математики
Рецензент: Евтюхов К.Н. – к., ф.- м.н., профессор кафедры физики
Рассмотрены УМК МТФ Протокол № от
ВВЕДЕНИЕ
Многим явлениям, в том числе экономическим, присуща многофакторная зависимость. Исследование таких зависимостей потребовало совершенствования математического аппарата, в частности, введения понятия функции нескольких переменных. В настоящих методических указаниях рассматриваются вопросы: - основные понятия; - частные производные; - дифференциал функции; - применение дифференциала к приближенным вычислениям; - производная по направлению, градиент; - экстремум функции нескольких переменных; - наибольшее и наименьшее значения функции; - условный экстремум, метод множителей Лагранжа; - понятие об эмпирических формулах, метод наименьших квадратов. Сведения из теории изложены лишь конспективно. Опущены строгие доказательства, однако практические вопросы рассмотрены довольно подробно, что необходимо для выполнения расчетно-графической работы. 1. Функции нескольких переменных, основные понятия
1) Если каждой точке М из некоторого множества Если множество Пример 1.1 Площадь прямоугольника со сторонами, длины которых равны Пример 1.2. Объем Пример 1.3. Величина силы притяжения
Следовательно, 2) Всякая функция от нескольких переменных становится функцией от меньшего числа переменных, если часть переменных зафиксировать, т.е. придать постоянные значения. Например, пусть мы имеем функцию трех переменных Если положить 3) Геометрическим изображением (графиком) функции двух переменных Линией уровня функции Пример 1.4. Соединив на карте поверхности Земли точки с одинаковой средней суточной температурой или давлением, получим соответственно изотермы и изобары, являющиеся важными исходными данными для прогноза погоды. 4) Пусть задана функция двух переменных Пример 1.5. Найти полное приращение функции
5) Частной производной функции от нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при условии, что последнее стремится к нулю. Таким образом, по определению, для функций двух переменных Пример 1.6. Пусть 6) Функция Полным дифференциалом функции Если функция Пример 1.7. Найти дифференциал функции
7) Частными производные второго порядка для функции Продолжая таким путем дальше, можно определить частные производные третьего порядка, четвертого, …. Справедливо следующее утверждение: если все входящие в вычисления частные производные непрерывны, то смешанные частные производные не зависят от последовательности дифференцирования, т.е. в случае непрерывности, например Пример 1.8. Пусть Градиент, дивергенция, ротор Если каждой точке М пространства или некоторой его области V поставлена в соответствие скалярная величина u(М), то говорят, что в этой области задано скалярное поле. В декартовой системе координат задание скалярного поля эквивалентно заданию функции трех переменных u(М) = u(x,y,z). Примерами скалярных полей могут служить поле температур данного тела, поле атмосферного давления и т.д. Пусть функция u(x, y, z) является непрерывно дифференцируемой в области V. В каждой точке этой области определен вектор, проекциями которого на оси координат являются значения частных производных функции u(x,y,z):
Вектор grad u направлен в сторону наибыстрейшего возрастания скалярного поля u(М), а длина градиента равна наибольшей скорости изменения поля u в точке М. Если каждой точке М некоторой области V поставлен в соответствие определенный вектор
а функции P(x,y,z), Q(x,y,z) и R(x,y,z) являются непрерывно дифференцируемыми в области V. В качестве примера векторного поля можно рассмотреть поле скоростей стационарного потока жидкости. Дивергенцией векторного поля
Ротором (вихрем) векторного поля
Все рассмотренные величины полей: grad u, div
Эту операцию можно записать кратко, вводя оператор Лапласа
Для векторного поля
12 |
|
 точек евклидова пространства ставится в соответствие по известному закону некоторое число
точек евклидова пространства ставится в соответствие по известному закону некоторое число 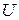 , то говорят, что на множестве
, то говорят, что на множестве  или
или  .
. и
и  , выражается формулой
, выражается формулой  .
. прямоугольного параллелепипеда с ребрами, длины которых равны
прямоугольного параллелепипеда с ребрами, длины которых равны  выражается формулой
выражается формулой  .
. двух материальных точек, имеющих массы
двух материальных точек, имеющих массы  и занимающих соответственно положение
и занимающих соответственно положение  и
и 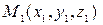 , согласно закону Ньютона равна
, согласно закону Ньютона равна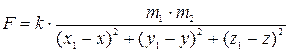 , где
, где 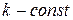 .
.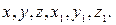
 .
.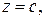 то мы получим функцию от двух переменных
то мы получим функцию от двух переменных  , если зафиксировать переменную
, если зафиксировать переменную  то получим функцию одной переменной
то получим функцию одной переменной  . Таким образом, в разных вопросах по желанию, функцию
. Таким образом, в разных вопросах по желанию, функцию  является, вообще говоря, поверхность в пространстве
является, вообще говоря, поверхность в пространстве  .
.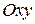 , для которых данная функция имеет одно и то же значение (изокривая). Ее уравнение
, для которых данная функция имеет одно и то же значение (изокривая). Ее уравнение 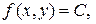 где
где  – некоторая постоянная. Поверхностью уровня функции
– некоторая постоянная. Поверхностью уровня функции  определяется уравнением
определяется уравнением  где
где  .
. . Если зафиксировать переменную
. Если зафиксировать переменную  , то разность
, то разность  называется частным приращением функции
называется частным приращением функции 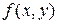 по переменной
по переменной  . Придавая приращение сразу двум переменным
. Придавая приращение сразу двум переменным  .
. , где
, где  изменяется от 2 до 2,2 и
изменяется от 2 до 2,2 и  от 1 до 0,9;
от 1 до 0,9;  ;
; 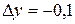 ;
;  ,
,  ;
; .
. ;
;  .
. , тогда
, тогда 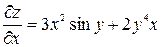 ;
; 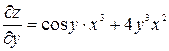 .
. называется дифференцируемой в данной точке
называется дифференцируемой в данной точке  если ее полное приращение в этой точке может быть представлено в виде
если ее полное приращение в этой точке может быть представлено в виде  где А, В – некоторые не зависящие от
где А, В – некоторые не зависящие от  числа, а
числа, а  и
и 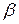 – бесконечно малые при
– бесконечно малые при  .
.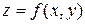 называется главная линейная часть полного приращения этой функции
называется главная линейная часть полного приращения этой функции  .
. , то
, то  и
и  . Тогда
. Тогда  , или
, или 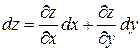
 .
. ,
,  ,
,  .
.
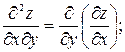

 .
. .
. , тогда:
, тогда:  ;
;  ;
; 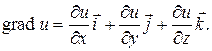
 , то говорят, что в этой области задано векторное поле. В декартовой системе координат задание векторного поля равносильно заданию трех скалярных функций: P(x,y,z), Q(x,y,z) и R(x,y,z) – проекций этого вектора на оси координат. Вектор
, то говорят, что в этой области задано векторное поле. В декартовой системе координат задание векторного поля равносильно заданию трех скалярных функций: P(x,y,z), Q(x,y,z) и R(x,y,z) – проекций этого вектора на оси координат. Вектор 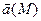 в этом случае записывается в виде
в этом случае записывается в виде

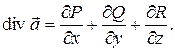
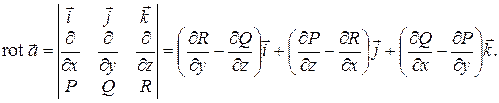
 и rot
и rot