|
|
Применение дифференциала к приближенным вычислениямПриращение функции
Этой формулой можно пользоваться для приближенного подсчета значения Пример 6.1. Высота конуса H=10 см, радиус основания R=5 см. Как изменится объем конуса при увеличении высоты на 2 мм и уменьшении радиуса основания на 2 мм. Решение. Объем конуса Подставив значения (в см) R=5, H=10, dR=–0.2, dH=0.2, получим
Пример 6.2.Вычислить приближенно число а=(1.04)2.03. Решение. Рассмотрим функцию f(x, y)=xy. Данное число a есть приращенное значение этой функции в точке P0(1, 20 при Его значения в точке P0(1, 2) при данных приращениях
поэтому имеем 7. Отыскание параметров эмпирических формул
Эмпирическими формулами часто пользуются в физических, химических и других естественных науках. Метод наименьших квадратов – один из лучших способов составления таких формул. Изложим идею этого метода для случая линейной зависимости двух величин. Пусть необходимо установить зависимость между двумя величинами
Будем рассматривать
Естественно в этом случае предположить, что между
где
Поскольку точки Следовательно, подставляя в формулу (2) вместо
где Требуется определить коэффициенты
была наименьшей. Если эта сумма окажется достаточно малой, то тогда и сами погрешности будут малыми по модулю. Подставляя равенства (3) в формулу (4), получаем:
Переменная величина
откуда определяем параметры Пример 7.1. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение Решение. Найдем необходимые для расчетов суммы
Нормальная система (5) имеет вид:
Решая эту систему, находим:
Так как
ВАРИАНТЫ ЗАДАНИЙ Вариант 1. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж. z=x2+y2–9xy+27; 0£ x£ 3, 0£ y£ 3. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки условного экстремума функции, используя метод множителей Лагранжа.
6. Одна сторона прямоугольника a=6 см, другая b=8 cм. Как изменится диагональ прямоугольника, если сторону a удлинить на 4 мм, а сторону b укоротить на 1 мм? Вариант 2. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж. z=x2+2y2+1; x³0, y³0, x+y£3. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки условного экстремума функции, используя метод множителей Лагранжа.
6. Вычислить sin440·cos290. Вариант 3. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж. z=3–2x2–xy–y2; x£1, y³0, y£x. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки условного экстремума функции, используя метод множителей Лагранжа.
6. Вычислить (0.97)2.02. Вариант 4. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж. z=x2+3y2+x–y; x³1, y³–1, x+y£1. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки условного экстремума функции, используя метод множителей Лагранжа.
6. Вычислить Вариант 5. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж.z=x2+2xy+2y2; –1£ x£ 1, 0£ y£ 2. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки условного экстремума функции, используя метод множителей Лагранжа.
6. Вычислить 0,97arctg Вариант 6. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж. z=5x2–3xy+y2+4; x³–1, y³–1, x+y£1. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки условного экстремума функции, используя метод множителей Лагранжа.
6. Вычислить Вариант 7. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж. z=10+2xy–x2; 0£y£4–x2. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки условного экстремума функции, используя метод множителей Лагранжа.
6.Вычислить sin590·cos320. Вариант 8. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж. z=x2+2xy–y2+4x; x£0, y£0, x+y+2³0. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки условного экстремума функции, используя метод множителей Лагранжа.
6. Вычислить 1.04·ln(1.02). Вариант 9. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж. z=x2+xy–2; 4x2–4£y£0. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки условного экстремума, используя метод множителей Лагранжа.
6. Вычислить Вариант 10. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж. z=x2+xy; –1£x£1, 0£y£3. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки условного экстремума, используя метод множителей Лагранжа.
6.Вычислить Вариант 11. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж. z=x2+y2–4xy–4; 0£ x£ 4, 0£ y£ 4. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки условного экстремума, используя метод множителей Лагранжа
6. Вычислить Вариант 12. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж. z=x2+2y2+4xy+1; –1£ x£ 1, 0£ y£ 2. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки экстремума функции, используя метод множителей Лагранжа.
6. Вычислить Вариант 13. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж. z=x3+y3–3xy; 0£ x£ 4, 0£ y£ 4. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки условного экстремума функции, используя метод множителей Лагранжа.
6. Закрытый ящик, имеющий наружные размеры 10 см, 8 см и 6 см, сделан из фанеры толщиной в 2 мм. Определить приближенно объем затраченного на ящик материала. Вариант 14. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж. z=x2–2y2+4xy–6x+5 в треугольнике, ограниченном осями Ох, Оу и прямой x+y=3. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки условного экстремума функции, используя метод множителей Лагранжа.
6. При измерении на местности треугольника АВС получены следующие данные: сторона а=100м Вариант 15. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж. z=x2–y2+4xy–6x–2y в треугольнике, ограниченном осями Ох, Оу и прямой x+y=3. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки условного экстремума функции, используя метод множителей Лагранжа f(x, y) = xy при 2x + 3y – 5 = 0. 6. Период Т колебания маятника вычисляется по формуле
Вариант 16. 1. Исследовать на экстремум функцию 2. Найти наибольшее и наименьшее значения функции z=f(x, y) в заданной замкнутой области. Сделать чертеж. z=2x3+4x2+y2–xy в области, ограниченной параболой y=x2, осью Оу (х³0) и прямой y=4. 3. Проверить, что rot rot
4. Опытные данные о значении переменных
В результате их выравнивания по параболе получено уравнение 5. Найти точки условного экстремума функции, используя метод множителей Лагранжа. 12 |
|
 и ее полный дифференциал
и ее полный дифференциал  связаны равенством
связаны равенством  , где
, где  – бесконечно малая более высокого порядка малости по сравнению с
– бесконечно малая более высокого порядка малости по сравнению с  при достаточно малых приращениях аргументов можно величиной
при достаточно малых приращениях аргументов можно величиной  пренебречь и считать
пренебречь и считать  . Это приводит к приближенному равенству
. Это приводит к приближенному равенству  , или подробно
, или подробно .
. по известным значениям функции
по известным значениям функции  и ее частным производным в данной точке P(x, y).
и ее частным производным в данной точке P(x, y). . Изменение объема приближенно заменим его дифференциалом
. Изменение объема приближенно заменим его дифференциалом  .
. .
. . Дифференциал данной функции
. Дифференциал данной функции  .
. ,
, .
. Под эмпирической формулой понимают формулу, составленную по данным, определенным в результате эксперимента. Получив в результате наблюдений
Под эмпирической формулой понимают формулу, составленную по данным, определенным в результате эксперимента. Получив в результате наблюдений  значений
значений  величины
величины  и
и  величины
величины  , ставят задачу отыскания такой аналитической зависимости между этими величинами, которая возможно мало отличалась бы от реальной зависимости между
, ставят задачу отыскания такой аналитической зависимости между этими величинами, которая возможно мало отличалась бы от реальной зависимости между 

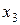

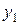



 и
и  как прямоугольные декартовы координаты точек на плоскости:
как прямоугольные декартовы координаты точек на плоскости:  ,
,  , …,
, …,  . Допустим, что эти точки расположены почти на некоторой прямой (рис. 1).
. Допустим, что эти точки расположены почти на некоторой прямой (рис. 1). , (1)
, (1) и
и  – некоторые постоянные коэффициенты (параметры), подлежащие определению. Равенство (1) можно записать в виде:
– некоторые постоянные коэффициенты (параметры), подлежащие определению. Равенство (1) можно записать в виде: , (2)
, (2) только приблизительно расположены на прямой, определяемой уравнением (1) или (2), то и эти формулы являются приближенными.
только приблизительно расположены на прямой, определяемой уравнением (1) или (2), то и эти формулы являются приближенными. , взятые из таблицы, получаем:
, взятые из таблицы, получаем: (3)
(3)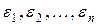 – некоторые числа, называемые погрешностями.
– некоторые числа, называемые погрешностями. были по возможности малыми по модулю. Согласно методу наименьших квадратов, подберем коэффициенты
были по возможности малыми по модулю. Согласно методу наименьших квадратов, подберем коэффициенты  (4)
(4) .
. является функцией двух переменных
является функцией двух переменных  ,
,  . Находя частные производные
. Находя частные производные  (5)
(5) . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью  ,
,  ,
,  ,
,  . Промежуточные вычисления оформим в виде вспомогательной таблицы.
. Промежуточные вычисления оформим в виде вспомогательной таблицы.


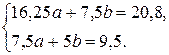
 ,
,  . Следовательно, зависимость между величинами
. Следовательно, зависимость между величинами  . Чтобы установить, какая их двух линий
. Чтобы установить, какая их двух линий 



 , то прямая
, то прямая 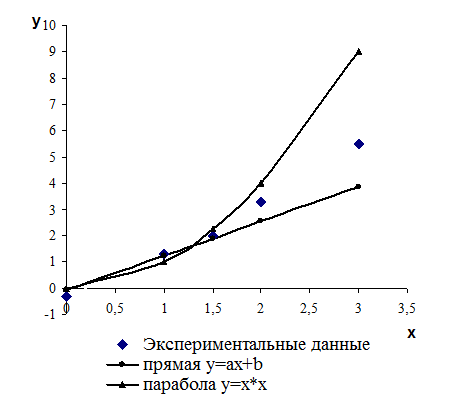
 .
. = grad div
= grad div 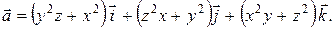
 . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью  при
при  .
. .
.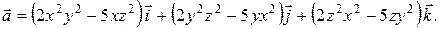
 . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью  при
при  .
. .
.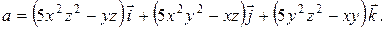
 . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью  при
при  .
. .
.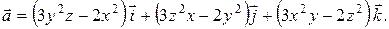
 . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью  при
при  .
. .
. .
.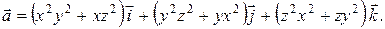
 . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью  при
при  .
. .
.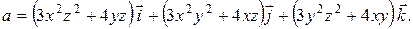
 . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью 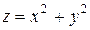 при
при  .
. .
. .
.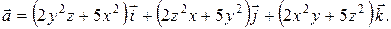
 . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью  при
при  .
. .
.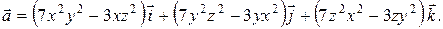
 . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью  при
при  .
. .
.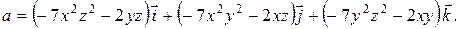
 . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью  при
при  .
. .
. .
.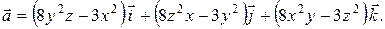
 . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью 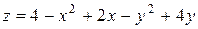 при
при  .
. .
. .
.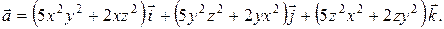
 . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью  при
при  .
. .
. .
.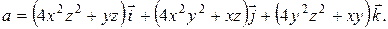
 . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью  при
при  .
. .
. .
.
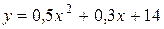 . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью  .
.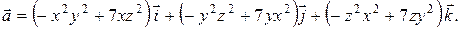
 . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью  при
при  .
. 2м, сторона b=200 м
2м, сторона b=200 м  .
.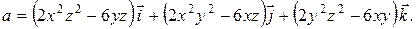
 , где l – длина маятника, g – ускорение силы тяжести. Найти погрешность в определении Т, получаемую в результате небольших ошибок
, где l – длина маятника, g – ускорение силы тяжести. Найти погрешность в определении Т, получаемую в результате небольших ошибок  и
и  при измерениях l и g.
при измерениях l и g. .
.
 . Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью
. Пользуясь методом наименьших квадратов, аппроксимировать эти данные линейной зависимостью