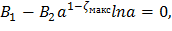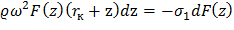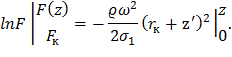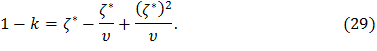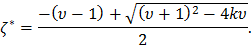Лопатка с показательным законом изменения площади сечения по высоте.

В этом случае

Распределение растягивающих напряжений по высоте лопатки определяется следующей зависимостью:

где σ₀ – напряжение в корне лопатки постоянного сечения при тех же величинах l и υ, что и для лопатки переменного сечения;

В отличие от лопаток с постоянным и линейным законами распределения сечений по высоте, в рассматриваемом случае максимальное растягивающее напряжение может достигаться в сечении выше корневого. Для определения его координаты исследуем функцию (22) на максимум, вычислив ее производную и приравняв к нулю.

Тогда

Прологарифмируем обе части последнего уравнения:

Если по формуле (23) получаются отрицательные значения ζ_макс, то наибольшее растягивающее напряжение достигается в корневом сечение (ζ_макс=0). Сама величина максимального растягивающего напряжения вычисляется с использованием функции (22):

Для количественного сравнения эффективности различных законов снижения растягивающих напряжений в корневой области рабочей лопатки используется коэффициент разгрузки

где σ_макс – наибольшее напряжение в лопатке переменного сечения; σ₀ – напряжение в корне лопатки постоянного сечения при тех же величинах l и υ, что и для лопатки переменного сечения. Лопатки с показательным законом изменения площадей имеют большую разгрузку (меньшие значение k) при равных a и υ по сравнению с рабочими лопатками с линейным законом изменения площадей.

Лопатка равной прочности.

Лопатка равной прочности имеет два участка. На первом участке, от корневого сечения до сечения с координатой z=z^*, закон изменения площадей выбирают так, чтобы растягивающее напряжение было постоянно по длине этого участка. На втором участке z^*≤z≤l лопатка имеет постоянное поперечное сечение.

Рассмотрим первый участок. Здесь растягивающие напряжения постоянны

где σ₁ – постоянное напряжение на первом участке. С учетом формулы (13) последнее выражение примет вид:

Продифференцировав, полученное соотношение преобразуем в обычное дифференциальное уравнение:

или после разделения переменных

Знак «минус» в приведенных уравнениях означает, что площадь поперечного сечения должна уменьшаться от корня к периферии, то есть при dz>0 → dF<0.

Проинтегрируем уравнение (24) в диапазоне от корня до рассматриваемого сечения с координатой z:

Таким образом, закон изменения площади поперечного сечения по высоте лопатки равной прочности окончательно представится в виде

где r=r_к+z – текущий радиус.

Определим координату z^* сечения, разделяющего первый и второй участки лопатки равной прочности. На первом участке напряжения остаются постоянными и являются наибольшими для рассматриваемой лопатки, то есть σ₁=σ_макс. Начиная с сечения с координатой z^* (второй участок), они начинают снижаться и достигают нуля на периферии. Таким образом, растягивающее напряжение в сечении z^* составит σ_макс. Площадь поперечного сечения на первом участке меняется согласно первому уравнению (25), на втором – остается постоянным и равным периферийному. Следовательно, в сечении с координатой z^* оно также будет равно периферийному.

На границе участков при z=z^* растягивающее напряжение и площадь поперечного сечения должны одновременно удовлетворять уравнениям (17) и (25):

где

Тогда

Согласно введенным ранее обозначениям имеем

где k – коэффициент разгрузки; а – отношение периферийной и корневой площадей поперечных сечений лопатки.

Рассмотрим второе уравнение из (26). Преобразуем комплекс в квадратных скобках:

В полученном выражении вынесем величину l за скобку

и с учетом ранее введенных обозначений получим

Рассмотрим комплекс

Тогда выражение (27) примет следующий вид:

где d_к и d_с – соответственно корневой и средний диаметры колеса.

Перегруппировав множители в полученном выражении

получим

Рассмотрим первое уравнение системы (26). Раскрыв скобки, получим

или

С учетом выражений (28) и (29), система (26) примет следующий вид:

Сравнивая первое и второе уравнения системы (30), легко установить взаимосвязь между параметрами k и a:

а координату ζ^* получим из решения первого уравнения:

Минимальные величины веерности, соответствующие длинным лопаткам последних ступеней турбины, составляют υ=2…3, а (υ-1) – всегда больше нуля. Поэтому из двух возможных решений уравнения (32) физический смысл имеет только

После элементарных преобразований окончательно получим

Лопатка равной прочности имеет наибольшую разгрузку из всех сравниваемых законов.