Геометрические множества и их размерность

Глава 1. ОБСУЖДЕНИЕ ОСНОВНЫХ ПОНЯТИЙ

Предмет инженерной графики

Потребность в использовании различных геометрических моделей, в особенности для изображения пространственных форм на плоскости, возникла из практических задач науки, техники, искусства и стала насущной необходимостью для многих отраслей человеческой деятельности. Любая область человеческой деятельности: научная, производственная, бытовая – всегда связана с накоплением, переработкой и передачей информации о процессах и явлениях окружающего мира. Для переработки и передачи такой информации используются разнообразные средства: устная речь и письменность, математические формулы и чертежи, картины и ноты, всевозможные знаки и символы, разнообразные технические устройства и многое другое. Одну и ту же информацию можно передавать различными способами. Так, сообщая сведения о форме технической детали, можно использовать словесное описание, рисунок, чертеж или макет. Если различные физические предметы, явления или процессы позволяют извлечь одну и ту же информацию, то принято говорить, что эти предметы, явления или процессы моделируют друг друга. Нетрудно понять, что без моделирования невозможно получить или передать какую-либо информацию об окружающем нас мире. Вот почему изучение различных моделей и методов моделирования имеет очень важное практическое значение. Общее число типов моделей, применяемых в науке, технике и искусстве необозримо велико. Среди всего многообразия моделей очень большое и самое широкое распространение получили математические модели. В настоящее время математические модели широко используются в науке и технике. Создание и внедрение автоматизированных систем проектирования и автоматизация производственных процессов во многом зависят от эффективных математических моделей этих процессов. Под математическими моделями обычно понимаются различные математические конструкции, пригодные для описания и воспроизведения взаимосвязей между параметрами моделируемого объекта. При конструировании математических моделей используют как аналитические, так и геометрические (или, как иногда говорят, синтетические) методы. В первом случае от условия поставленной задачи переходят к чисто количественному описанию и устанавливают зависимость между действующими числами, во втором случае от условия задачи переходят к геометрическому (пространственному) описанию и устанавливают зависимость между действующими геометрическими образами (фигурами). На практике часто бывает очень полезно совместное использование тех и других методов. В том случае, когда модели строятся на основе геометрических понятий, речь идет о геометрических моделях, а методы их конструирования называют геометрическим моделированием.

Любое производство невозможно без предварительной разработки технической документации. Неотъемлемой частью любого проекта являются чертежи, схемы или карты. Большинство используемых чертежей построено в системе ортогональных проекций. Теория построения таких чертежей изложена в начертательной геометрии. Начертательная геометрия плодотворно питает другие области знаний. По образному выражению Д.И. Менделеева, «Геометрические знания составляют основу всей точной науки». Геометрия всегда “помогала разуму познать истину”, являясь “правительницей умственных изысканий”.

Чертеж как язык техники дает геометрическую информацию о форме деталей узла, принципе работы узла, перемещении деталей относительно друг друга, преобразовании движений, возникновении усилий, напряжений, преобразовании энергии в механическую работу и т.п. Для передачи различной информации чертежи дополняют различными знаками и символами, а для их словесного описания используются новые понятия, в основу формирования которых положены фундаментальные понятия физики, химии и математики.

Краткая история развития

Начальные сведения о методах изображений геометрических форм, применялись древними греками. Трехмерное пространство, подчиняющееся правилам Евклида, стали называть евклидовым пространством. Это пространство и ныне является объектом изучения в геометрии средней школы. Большой прогресс в области изображений произошел в эпоху Возрождения. Развернувшееся в это время строительство зданий и сооружений расширило применявшиеся в античном мире приемы построения изображений. Архитекторы, скульпторы, живописцы встали перед необходимостью создания на геометрической основе учения о перспективе. Новую эпоху в истории развития методов изображения открыл знаменитый французский геометр, инженер, педагог, общественный деятель времен великой французской революции Гаспар Монж (1746 – 1818). Г. Монж дал общий метод решения стереометрических задач геометрическими построениями на плоскости, фактически создав тем самым новую науку – начертательную геометрию. В развитии начертательной геометрии как науки Г. Монж сыграл выдающуюся роль. Он систематизировал и обобщил различные способы изображения пространственных форм на плоскости в двух проекциях, рассматривая чертеж (эпюр) как результат от совмещения двух взаимно перпендикулярных плоскостей проекций. Начертательная геометрия стала учебной дисциплиной и заняла прочное место в технической школе.

В России с 1810 года преподавание начертательной геометрии начал вести французский инженер К. И. Потье, ученик Г. Монжа (петербургский институт корпуса инженеров путей сообщения). Первым русским профессором начертательной геометрии был Я. А. Севостьянов. Его учебник “Основания начертательной геометрии” стоял на уровне лучших европейских курсов. Классические труды по начертательной геометрии создал профессор Валериан Иванович Курдюмов, изложивший с исчерпывающей полнотой для своего времени теорию ортогональных проекций, аксонометрии, проекций с числовыми отметками. Академик Евграф Степанович Федоров разработал способы графического представления сложных составов минералов и пород, определения углов простирания и падения пластов горных пород. Идеи Е. С. Федорова нашли применение в физической химии, петрографии и других науках, раскрыли возможность развития теории изображения многомерных пространств. Многочисленные труды по начертательной геометрии принадлежат ученику В. И. Курдюмова профессору Николаю Алексеевичу Рынину. Он показал широту применения начертательной геометрии в самых различных областях науки и техники, его работы были связаны с решением практических задач графической статики, механики, аэрофотосъемки, кинематографии. Значительный вклад в становление этой науки внесди Алексей Константинович Власов, Нил Александрович Глаголев, Александр Иванович Добряков. Дмитрий Иванович Каргин, Николай Алексеевич Попов, Владимир Осипович Гордон, Михаил Яковлевич Громов, Николай Федорович Четверухин и Иван Иванович Котов.

Оформление начертательной геометрии в качестве самостоятельной научной дисциплины произошло благодаря интенсивному развитию одной области ее практического применения – технического черчения. За столетний период с опубликования Г. Монжем (1795 г.) первого систематизированного труда, начертательная геометрия окончательно определилась в границах своих исследований. За это время получили законченное развитие основные разделы дисциплины: ортогональные проекции, аксонометрия, перспектива, проекции с числовыми отметками. В этот период установился и окончательно окреп союз начертательной геометрии с теми областями практической деятельности человека, где особо нуждались в использовании графической документации: строительство, архитектура, машиностроение, горное дело. Классическая начертательная геометрия, таким образом, оказалась неразрывно связанной с тремя основными предпосылками: трехмерное исходное пространство, плоская двумерная картина и соединяющая их операция линейного проецирования. Предметом начертательной геометрии стали считать теорию изображения пространственных форм на плоскости. Не следует считать, что на протяжении Х1Х века, все без исключения исследования в области начертательной геометрии строго и неуклонно укладывались в установленное русло. Прежде всего, давала о себе знать математическая родословная теории изображений. Проективная геометрия, возникшая на основе начертательной геометрии и считавшаяся ее подсобным ответвлением, вскоре далеко обогнала последнюю в своем чисто математическом развитии и стала оказывать на нее сильное постоянное влияние. Создалось так называемое проективное направление в начертательной геометрии. Создание и распространение в конце Х1Х века фотографической аппаратуры послужило основой для возникновения фотограмметрии и стереофотограмметрии, а также связанных с этим геометрических задач. Практические запросы стереофотограмметрии способствовали разработке в общей форме алгоритма решения задачи по построению третьего проекционного изображения по двум заданным проекционным изображениям предмета. Следует отметить, что если первый приток новых идей начертательная геометрия получила благодаря своему математическому происхождению, то дальнейшее обогащение ее содержания пришло со стороны практических приложений. Уже в начале ХХ века область практического приложения начертательной геометрии значительно расширилась, появились работы Е. С. Федорова по применению геометрических изображений в кристаллографии и горной геометрии. В середине прошлого столетия зародилась новая ветвь начертательной геометрии – многомерная начертательная геометрия. Дальнейшие теоретические успехи начертательной геометрии неотрывно связаны с обогащением ее содержания наиболее общими понятиями и идеями теории моделирования и теории информации. Следует отметить, что нарастание потока научной информации, разнообразные по своему направлению и содержанию научные исследования значительно расширили круг традиционно принятых в классической начертательной геометрии понятий и представлений. В результате возникла естественная потребность зафиксировать новую научную ситуацию с помощью общего термина «геометрическое моделирование», предложенного, профессором К. И. Вальковым, который позволяет, во-первых, суммировать и оценить уже проделанную научно-исследовательскую работу, а, во-вторых, прогнозировать пути дальнейшего ее развития. Автоматизация производственных процессов возможна только при их формальных описаниях. Эффективность использования вычислительной техники во многом определяется развитием теории геометрического моделирования, занимающейся изучением способов построения геометрических моделей, предназначенных для передачи и переработки геометрической информации.

Геометрические множества и их размерность

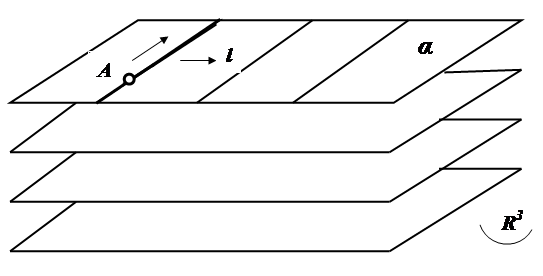
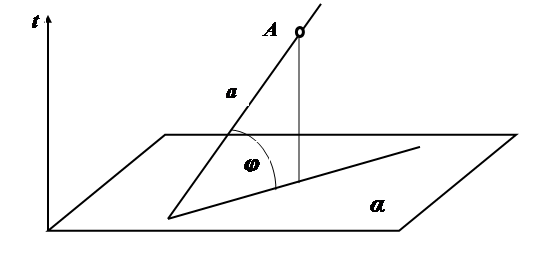
Основой всех геометрических представлений является понятие о пространстве. Пространство мыслится как множество точек, прямых, плоскостей и других геометрических образов. Простейшим реальным объектом, который удобно описывать и моделировать с помощью геометрических представлений, является совокупность всех наблюдаемых физических тел, вещей и предметов. Эта совокупность заполняет физическое пространство, которое можно рассматривать как исходный объект, подлежащий изучению, геометрическое пространство – как его математическую модель, Физические связи и отношения между реальными объектами заменяются позиционными и метрическими отношениями геометрических образов. Описание условий реальной задачи в геометрических терминах является очень ответственным и самым сложным этапом решения задачи, требующим сложной цепи умозаключений и высокого уровня абстракции, в результате которого реальное событие облекается в простую геометрическую конструкцию. Важнейшей характеристикой геометрического пространства является его размерность. Самый простой геометрический образ – точка. Под точкой понимается простейший элемент, занимающий положение в пространстве, но не имеющий измерений. Размерность точки равна нулю. Точкой моделируют объекты, размеры которых в данный момент не имеют значения. В одном случае точкой может моделироваться атом, молекула, а в другом случае – спутник, планета. Движение точки А образует линию (в частности прямую l). Так, например, движение самолета образует светящуюся траекторию. Для того чтобы определить положение точки на прямой линии, необходимо задать один параметр. Отсюда размерность линии равна единице (рис.1.1). Движение линии образует двухмерную поверхность (в частности плоскость α). Для определения положения точки на поверхности необходимы два параметра. Движение поверхности образует трехмерное пространство. Этот ряд рассуждений может быть продолжен дальше до n-мерного пространства. Многомерное пространство используется для описания и моделирования таких явлений, которые зависят от многих (параметров). Например, для описания кинематических явлений, т.е. для моделирования систем, изменяющих свое положение в пространстве и во времени, применяется четырехмерное пространство событий. Движущийся объект изображается мировой линией, каждой точке которой соответствует положение объекта в определенный момент времени. Рассмотрим пример на плоскости α движется объект А со скоростью V (рис. 1.2).

Рис. 1.1. Модель точки, прямой, плоскости и трехмерного пространства

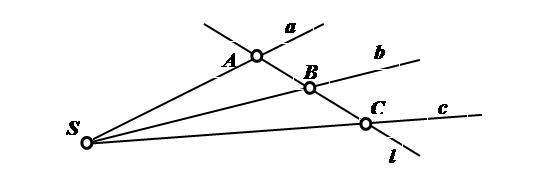
Рис. 1.2. Пространство событий

Геометрическая модель представляет собой пространственную мировую линию а, каждой точке которой соответствует положение объекта в определенный момент времени. Если скорость равномерная, то мировая линия прямая. Угол наклона мировой линии φ характеризует величину скорости, чем меньше угол, тем больше скорость. При φ = 90^о объект неподвижен. В геометрии различают линейные и криволинейные образы. К линейным геометрическим образам относятся точка, прямая линия, плоскость, пучок прямых линий, связка прямых линий, пучок плоскостей, конгруэнция. Для определения положения точки и плоскости в пространстве необходимо три параметра. Для выделения прямой линии в пространстве необходимо четыре параметра. К криволинейным образам относятся плоские и пространственные кривые линии и поверхности. Наибольшую известность получили такие замечательные плоские кривые линии: окружность, эллипс, парабола, гипербола, синусоида, спираль Архимеда, эвольвента, лемниската, кардиоида, конхоида, циклоида, эпициклоида и гипоциклоида. Широкое распространение получили поверхности вращения: цилиндр, конус, сфера, тор, косая плоскость, однополостный гиперболоид, а также винтовые поверхности.

Необходимо мыслить о точках, прямых, плоскостях как о равноправных элементах, заполняющих трехмерное пространство. Два элемента, связанные отношением взаимной принадлежности, называются инцидентными. Две точки определяют положение прямой. Три точки, точка и прямая линия или две пересекающиеся прямые линии задают плоскость. В свою очередь, единственную точку на плоскости определяют две прямые линии, в пространстве – три плоскости или прямая и плоскость. Четыре точки в общем случае не лежат в одной плоскости и задают двугранный угол. С помощью точек и прямых можно определить положение других геометрических образов. В общем случае две произвольные прямые линии в трёхмерном пространстве скрещиваются. Множество точек, принадлежащих какой-либо прямой линии, называется прямолинейным рядом точек. Точки, заполняющие кривую линию, образуют криволинейный ряд точек. Плоскость, как множество точек, называется плоским полем точек, а как множество прямых – плоским полем прямых. Если в плоскости зафиксировать точку, то множество прямых линий, проходящих через нее, образует пучок прямых (рис. 1.3). Через точку в пространстве можно провести множество прямых линий, пересекающих заданную прямую линию. Это множество является пучком прямых линий на плоскости.

Рис. 1.3. Пучок прямых и ряд точек

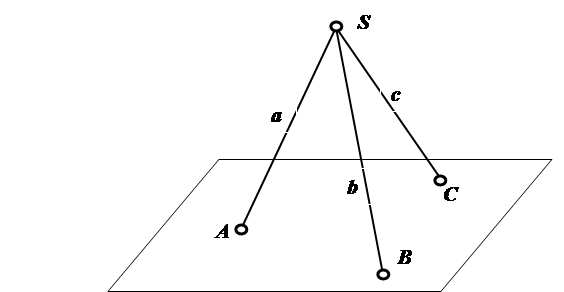
В случае, когда точка зафиксирована в трехмерном пространстве, то множество прямых линий, проходящих через нее, образует связку прямых линий (рис. 1.4).

Рис. 1.4. Связка прямых и плоское поле точек

Множество плоскостей, проходящих через фиксированную точку пространства, образует связку плоскостей, а множество плоскостей, проходящих через фиксированную прямую, образует пучок плоскостей (рис. 1.5).

Рис. 1.5. Пучок плоскостей и ряд точек

Линейной конгруэнцией называется множество прямых линий, пересекающих две фиксированные скрещивающие прямые линии. Однополостным гиперболоидом называется множество прямых линий пересекающих три заданные скрещивающие прямые линии. Чтобы определить размерность какого-либо множества геометрических образов, необходимо сопоставить его элементы с элементами другого множества, размерность которого уже известна. Так, например пучок прямых (множество прямых, проходящих через одну точку на плоскости) и пучок плоскостей (множество плоскостей, проходящих через одну прямую) являются одномерными множествами, так как эти множества можно взаимно однозначно сопоставить с рядом точек на прямой линии (рис. 1.3 и рис.1.5); размерность связки прямых линий (множества прямых, проходящих через одну точку в пространстве) равна двум, так как это множество можно взаимно однозначно сопоставить с плоским полем точек (рис. 1.4). Иногда для исчисления размерности используется термин число параметров. Таким образом, можно сказать, что размерность пространства определятся количеством независимых переменных (параметров, координат), необходимых для выделения одного элемента множества. Следует заметить, что любой геометрический элемент может рассматриваться пространством, и наоборот, любое пространство может являться элементом другого пространства. Заметим, что любое определение не является жестко фиксированным и носит относительный характер. В геометрии очень широко распространено понятие о геометрических множествах, обладающих определенным свойством. Так, например, геометрическим множеством точек, удаленных от данной точки на заданное расстояние, является сфера. Геометрическим множеством точек, равноудаленных от концов отрезка, на плоскости является прямая линия, в пространстве – плоскость. Геометрическим множеством прямых линий, равно наклоненных к заданной прямой линии и пересекающих ее в одной точке, является коническая поверхность вращения. Эта поверхность получается при вращении прямой линией вокруг оси, пересекающейся с ней под каким-то углом. Геометрическим множеством прямых линий, параллельных заданной прямой линии и равноудаленных от неё на заданное расстояние является цилиндрическая поверхность вращения. Эта поверхность получается при вращении прямой линией вокруг оси, параллельной данной линии. При вращении окружности вокруг её диаметра образуется сфера. Геометрическим множеством прямых линий, пересекающих три скрещивающиеся прямые линии, является однополостный гиперболоид вращения. Геометрическим местом точек пространства, равноудаленных от заданных прямых параллельных линий является плоскость, перпендикулярная к плоскости заданных прямых линий и проходящая по средине между ними. Геометрическим местом точек пространства, равноудаленных от заданных плоскостей является биссекторная плоскость. В геометрии существуют очень важные понятия о касательных и нормалях. Касательной прямой линией t к плоской кривой линии f в точке А называется предельное положение секущей прямой линии (рис. 1.6). Нормалью n к кривой линии f называется перпендикуляр к касательной t.

Рис. 1.6. Касательная и нормаль к плоской кривой линии

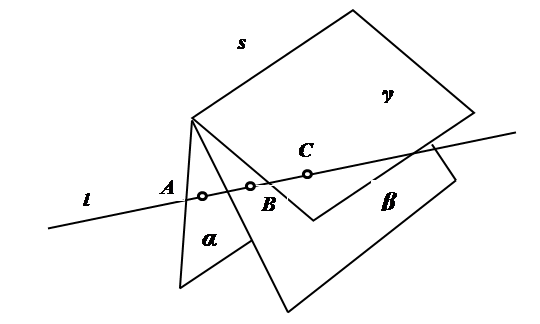
Известно, что в каждой точке А пространственной кривой (кривой двоякой кривизны) q существует единственная касательная t, главная нормаль n, бинормаль s, соприкасающаяся плос­кость α, спрямляющая плоскость β и нормальная плоскость γ, образующие трехгранник Френе (рис. 1.7). Направляющая кривая линия вблизи точки располо­жена по разные стороны от соприкасающейся плоскости.

Рис. 1.7. Трехгранник Френе

Касательной плоскостью к поверхности называется предельное положение секущей плоскости. Нормалью к поверхности называется перпендикуляр к касательной плоскости. Плоскость касается сферы в одной точке. Плоскость касается конуса и цилиндра по образующей прямой линии. Через точку в пространстве можно провести множество прямых линий, касательных к сфере. Через точку в пространстве можно провести множество плоскостей, касательных к сфере. Эти плоскости являются касательными к конической поверхности с вершиной в заданной точке. Через точку в пространстве можно провести две касательные плоскости, касательные к двум сферам. Через точку в пространстве можно провести две касательные плоскости к цилиндрической и конической поверхности. Через прямую линию в пространстве можно провести две касательные плоскости к сфере, если прямая линия не пересекается со сферой. Если прямая линия касается сферы, то через неё можно провести только одну касательную плоскость. Через прямую линию в пространстве можно провести две касательные плоскости к цилиндру или конусу, если прямая линия параллельна образующим цилиндра или проходит через вершину конуса. Касательную плоскость можно провести к цилиндру и сфере, к конусу и сфере, к двум цилиндрам с параллельными образующими, к двум конусам с общей вершиной, к двум и трем сферам.