|
|
Момент инерции. Аналогия между поступательным и вращательным движениямиЛабораторная работа №21 Изучение движения маятника Максвелла Цель работы: изучение основных законов и характеристик вращательного движения и сложного поступательно-вращательного движения маятника Максвелла. Приборы и принадлежности: прибор «Маятник Максвелла», набор из трех металлических накладных колец, штангенциркуль.
Теоретическая часть Вращение твердого тела вокруг неподвижной оси. Угловая скорость, угловое ускорение При вращении твердого тела вокруг закрепленной оси траектории всех частиц являются окружностями с центрами на этой оси. Все частицы тела совершают плоское движение; при этом скорости и ускорения отдельных точек тела различны: чем дальше точка находится от оси, тем быстрее она движется и тем больше должно быть ее ускорение. В этом случае разумно ввести такие кинематические характеристики вращения тела, как угловая скорость и угловое ускорение. Рассмотрим произвольную точку А в объеме тела, а начало отсчета поместим в произвольной точке на оси вращения, тогда радиус-вектор r точки А относительно начала отсчета будет иметь постоянную длину. Разложим его на две компоненты — поперек и вдоль оси вращения r = r + r, где r — постоянная часть, r. — переменная. С течением времени при вращении модуль r не меняется, а меняется лишь его направление. Это направление можно однозначно описать углом φ относительно произвольного направления х, выбранного за нулевое направление. Угол φ > 0, если он отсчитывается против часовой стрелки при наблюдении, когда ось вращения z направлена к нам, и φ < 0 в противном случае.
Угловой скоростью вращения вокруг оси z назовем скорость изменения утла ориентации перпендикулярной оси вращения компоненты радиус-вектора точки:
Угловым ускорением вращения вокруг оси z назовем скорость изменения угловой скорости вращения вокруг этой оси:
Важны не только сами величины
Вектор
Точку приложения вектора Связь между угловой и линейной скоростями вращения точек твердого тела можно записать так: ν= Вектор Размерности введенных угловой скорости и углового ускорения следующие: [
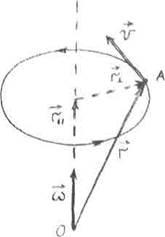
Момент инерции. Аналогия между поступательным и вращательным движениями Выделим в твердом теле, вращающемся вокруг неподвижной оси, N маленьких «кусочков» массой mi и рассмотрим вращение одного из них с номером i. Пусть он находится на расстоянии ri от начала отсчета, расположенного на оси вращения, и пусть его угловая скорость вращения Li = ri x mivi = ri x mi[ Раскрывая двойное векторное произведение, получим: Li = mi{ Составляющая момента импульса выделенного «кусочка» вдоль оси вращения запишется как Li = mi Тогда составляющая момента импульса всего тела вдоль оси вращения: L = I Составляющая момента импульса твердого тела вдоль неподвижной оси вращения пропорциональна угловой скорости. Коэффициент пропорциональности I называется моментом инерции твердого тела: I = где ri – это расстояние от оси вращения до рассматриваемой точки твердого тела. Момент инерции I – величина, зависящая от распределения массы тела относительно оси вращения. Отметим, что вектор момента импульса твердого тела раскладывается на две составляющие – вдоль и поперек оси вращения: L = L + L. Составляющая L не зависит напрямую от Запишем уравнение вращательного движения твердого тела вокруг неподвижной оси:
Поэтому для тела, вращающегося вокруг оси симметрии:
Если I=const, то
Таким образом, произведение момента инерции твердого тела на угловое ускорение равно моменту внешних сил относительно неподвижной оси вращения. Последняя формула является основным законом динамики вращательного движения твердого тепа относительно неподвижной оси. Из него следует, что в отсутствии момента внешних сил угловая скорость вращения твердого тела остается постоянной. Или иначе, если М = 0 (в случае замкнутой системы), то L=const, что представляет собой закон сохранения момента импульса: момент замкнутой системы сохраняется. Говоря о моменте инерции тела, всегда указывают, относительно какой именно оси он определен (в нашем случае это ось z, направленная вертикально вверх). Момент инерции того же тела относительно какой-либо другой оси примет иное течение. Сохраняется только общее правило его вычисления; берется сумма по элементам массы, составляющим тело, умноженным на квадраты расстояний этих элементов массы до оси вращения. В случае непрерывного распределения масс с плотностью
Если тело однородно, то его плотность во всех точках постоянна, и тогда
Можно легко проследить аналогию между поступательным и вращательным движением твердого тела:
12 |
|

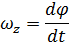
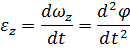
 и
и  , но и направление оси вращения в пространстве, поэтому условились вводить понятие векторов угловой скорости и углового ускорения:
, но и направление оси вращения в пространстве, поэтому условились вводить понятие векторов угловой скорости и углового ускорения: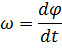
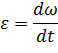
 направлен вдоль оси вращения так, что его направление образует с направлением вращения правый винт. Вектор
направлен вдоль оси вращения так, что его направление образует с направлением вращения правый винт. Вектор  (угловое перемещение изображаемое вектором) направлен так же, как и вектор
(угловое перемещение изображаемое вектором) направлен так же, как и вектор  направлен так же, как и вектор а, если при вращении точки вращающегося тела ускоряются, и он направлен в противоположную сторону, если при вращении точки вращающегося тела замедляются.
направлен так же, как и вектор а, если при вращении точки вращающегося тела ускоряются, и он направлен в противоположную сторону, если при вращении точки вращающегося тела замедляются.
 хr
хr ri2– ri2} = mi
ri2– ri2} = mi  ,
, .
. или
или  .
. в твердом теле сумма заменится на интеграл по всему объему тала:
в твердом теле сумма заменится на интеграл по всему объему тала: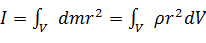 .
. можно вынести из-под знака интеграла:
можно вынести из-под знака интеграла: .
.