|
|
Вычисление момента инерции для тел симметричной формыНахождение момента инерции – вычислительная задача. Найдем моменты инерции для простейших геометрически правильных форм твердого тела, масса которого равномерно распределена по объему. Момент инерции обруча относительно оси перпендикулярно его плоскости и проходящей через его центр. Обруч будем считать бесконечно тонким, т. е. толщиной обода можно пренебречь по сравнению с радиусом R. Поскольку в этой системе все массы находятся на одинаковом расстоянии от оси вращения, R2 можно вынести из-под знака интеграла:
где
Момент инерции диска относительно оси, перпендикулярной его плоскости и проходящей через центр. Диск будем считать бесконечно тонким, т. е. его толщина много меньше радиуса R. Момент инерции, согласно определению, величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей. Разобьем диск на бесконечно тонкие кольца радиусом г и шириной dr.
Площадь выделенного кольца равна произведению его длины окружности на ширину кольца: 2πrdr. Поскольку масса m диска распределена равномерно, то масса единицы площади диска равна m/(πR2). Масса кольца: dm = 2πrdr(m/πR2) = (2m/πR2)rdr. Момент инерции кольца: dI = drm2 = (2m/πR2)r3dr. Просуммируем моменты инерций всех таких колец:
Момент инерции шара относительно его диаметра.
Объем диска dVz равен его площади, умноженной на толщину: dVz = πr2dz. Массу выделенного диска dm находим, разделив массу шара т на его объем 4πR3/3 и умножив на объем диска:
Момент инерции диска в данном случае:
Момент инерции шара находится интегрирование по всем таким дискам:
Момент инерции тонкого стержня относительно оси вращения, проходящей через его середину перпендикулярно стержню. Пусть стержень имеет длину l. Направим ось х вдоль стержня. Начало координат пусть находится на середине стержня. Возьмем элемент стержня длиной dx, находящийся на расстоянии х от оси вращения. Его масса равна dm = (m/l)dx, а момент инерции стержня – dI = dmx2 = (m/l)x2dx Отсюда находим момент инерции стержня:
Маятник Максвелла Для определения момента инерции тел с вращательной симметрией используется маятник Максвелла. В нем исследуемое тело совершает сложное плоско-параллельное движение. Небольшой диск (маховичок), насаженный туго на ось, опускается под действием силы тяжести на двух нитях, предварительно намотанных на ось маховичка. Нити во время движения разматываются до полной длины, раскрутившийся маховичок продолжает вращательное движение в том же направлении и наматывает нити на ось, вследствие чего он поднимается вверх, замедляя при этом вращение. Дойдя до верхней точки, диск опять опускается вниз и т. д. Маховичок будет совершать колебания вверх и вниз, поэтому устройство называют маятником. Движение маятника Максвелла можно рассматривать как сложное, состоящее из поступательного движения вниз и вращательного вокруг своей оси симметрии. Поступательное движение описывается соответствующим уравнением динамики, которое мы запишем в проекциях на вертикальную ось, совпадающей по направлению с вектором g, где g – ускорение свободного падения: mа = mg — 2Т. Уравнение динамики для вращательной составляющей этого движения имеет следующий вид в проекциях на горизонтальную ось, совпадающей по направлению с вектором М: Iε = M, где m – масса маятника, 2T – суммарное натяжение нитей подвеса, I – момент инерции маятника относительно горизонтальной оси, ε – угловое ускорение, М – момент натяжения нитей, равный 2TR, где R – радиус оси подвеса маятника. Взаимосвязь между поступательным и вращательным движениями: а =εR, а=2h/t2, где h – путь, проходимый маятником от верхней точки до нижней, t – время движения маятника при прохождении пути h. Из написанных выше уравнений получаем следующее: I = mR2*(gt2/2h – 1) = md2/4*(gt2/2h – 1) Эта формула выражает момент инерции маятника Максвелла, который состоит из оси, диска и кольца. Таким образом, момент инерции маятника Максвелла можно записать в виде: I = Iо + Iд + Iк, где I – момент инерции маятника Максвелла, Iо – момент инерции оси подвеса, Iд – момент инерции диска, Iк – момент инерции накладного кольца. Аналогично можно записать и массу маятника Максвелла: m = mо + mд + mк, где m – масса маятника Максвелла, mо – масса оси подвеса, mд – масса диска, mк – масса съемного кольца. Выразим момент инерции кольца: Iк = I - Iо - Iд. Для исключения неизвестных величин проведем эксперимент с кольцами разной массы. Запишем для каждого кольца выражение Iк1 = I1 - Iо - Iд, Iк2 = I2 - Iо - Iд Так как внешние и внутренние радиусы колец одинаковы, то:
Решив систему уравнений, получим:
Для третьего кольца момент инерции будет равен:
Таблица 1Формулы расчета момента инерции
где
Экспериментальная часть Для определения момента инерции тел вращения будем использовать специальную установку – маятник Максвелла.
1 – основание, 2 – стойка, 3 – неподвижный верхний кронштейн, 4 – подвижный кронштейн, 5 – электромагнит, 6 – вороток с фиксатором, 7 – фотодатчик, 8 – ось с закрепленным на ней диском, 9 – бифилярный подвес, 10 – сменное металлическое кольцо, 11 – миллисекундомер.
Упражнение 1. Определение момента инерции маятника Максвелла. 1. Включаем в сеть шнур питания миллисекундомера и нажимаем на кнопку «сеть», расположенную на лицевой панели секундомера. При этом загораются лампочки фотодатчика и цифровые индикаторы миллисекундомера. 2. Устанавливаем на диске маятника кольцо с массой mк1.
3. По шкале на стойке 2 определяем ход маятника h от верхней точки до нижней. h = 23,2 см = 0,232 м 4. Вращая маятник, зафиксируем его в верхнем положении при помощи электромагнита, следя за тем, чтобы нить наматывалась на ось виток к витку. Нажимаем на кнопку «сброс» и убеждаемся, что индикатор секундомера обнулился. 5. Плавно нажимаем кнопку «пуск» на милисекундомере и измеряем время хода маятника t. Измерения повторяем 10 раз. Находим среднее значение хода маятника tср. 6. Проделываем пп. 2-5 с кольцами массой mк2 и mк3. 7. Измеряем штангенциркулем радиус оси Ro, радиус диска Rд, внешний Rвнеш и внутренний Rвн радиусы трех колец с разной массой. Измеряем длину оси λ, толщину диска bд и толщину накладных колец bк. Масса диска с осью равна 120г. Измерения выполнены с учетом поправки на 9,9 мм. 8. Результаты всех измерений оформляем в виде таблицы.
9. По формулам рассчитаем экспериментальные значение момента инерции маятника Максвелла с первым, вторым и третьим кольцом. I = mR2*(gt2/2h – 1)
10. Вычислим доверительный интервал в определении момента инерции маятника и относительную ошибку согласно теории погрешности для всех трех случаев.
11. Запишем конечные результаты для моментов инерции маятника Максвелла с первым, вторым и третьим кольцом с учетом доверительного интервала и относительной погрешности.
12. По формулам рассчитаем теоретические значения момента инерции маятника Максвелла с первым, вторым и третьим кольцом.
13. Вычислим относительную ошибку измерения: Е = ∆ х / хист. * 100%
Упражнение 2. Определение момента инерции накладных колец. 1. Включаем в сеть шнур питания миллисекундомера и нажимаем на кнопку «сеть», расположенную на лицевой панели секундомера. При этом загораются лампочки фотодатчика и цифровые индикаторы миллисекундомера. 2. Устанавливаем на диске маятника кольцо с массой mк1. 3. По шкале на стойке 2 определяем ход маятника h от верхней точки до нижней. h = 23,2 см = 0,232 м 4. Вращая маятник, зафиксируем его в верхнем положении при помощи электромагнита, следя за тем, чтобы нить наматывалась на ось виток к витку. Нажимаем на кнопку «сброс» и убеждаемся, что индикатор секундомера обнулился. 5. Плавно нажимаем кнопку «пуск» на милисекундомере и измеряем время хода маятника t. Измерения повторяем 10 раз. Находим среднее значение хода маятника tср. 6. Проделываем пп. 2-5 с кольцами массой mк2 и mк3. 7. Измеряем штангенциркулем радиус оси Ro, радиус диска Rд, внешний Rвнеш и внутренний Rвн радиусы трех колец с разной массой. Измерения выполнены с учетом поправки на 9,9 мм. 8. Результаты всех измерений оформляем в виде таблицы.
9. По формулам рассчитаем экспериментальные значения момента инерции маятника Максвелла с первым, вторым и третьим кольцом.
10. Вычислим доверительный интервал в определении момента инерции маятника и относительную ошибку согласно теории погрешности для всех трех случаев.
11. Запишем конечные результаты для моментов инерции маятника Максвелла с первым, вторым и третьим кольцом с учетом доверительного интервала и относительной погрешности.
12. По формуле рассчитаем теоретические значения момента инерции первого, второго и третьего кольца:
13. Вычислим относительную ошибку измерения: Е = ∆ х / хист. * 100%
Вывод: 12 |
|
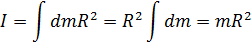
 – полная масса обруча.
– полная масса обруча.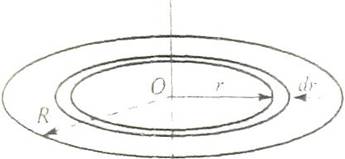
 .
.
 .
.
 .
. .
. .
.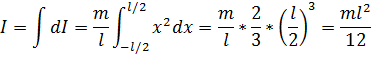
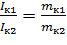 .
. ,
, .
.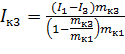 .
.


 кг/м3 – плотность материала, из которого изготовлена ось и диск;
кг/м3 – плотность материала, из которого изготовлена ось и диск;  кг/м3 – плотность материала кольца; Ro – радиус оси; Rд – радиус диска; Rвнеш и Rвн – внешний и внутренний радиусы кольца; λ – длина оси; bд – толщина диска; bк – толщина накладного кольца.
кг/м3 – плотность материала кольца; Ro – радиус оси; Rд – радиус диска; Rвнеш и Rвн – внешний и внутренний радиусы кольца; λ – длина оси; bд – толщина диска; bк – толщина накладного кольца.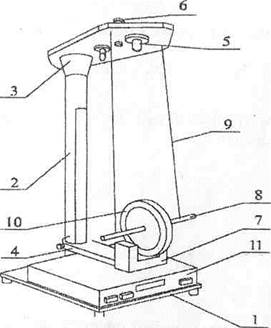
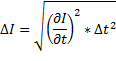
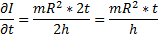











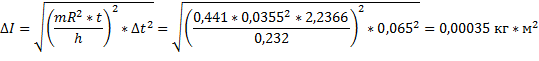

 , кг*м2
, кг*м2
 , кг*м2
, кг*м2
 , кг*м2
, кг*м2
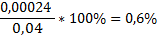


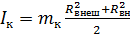 .
.