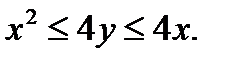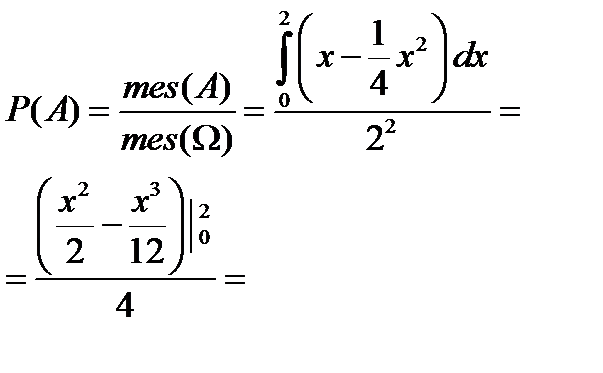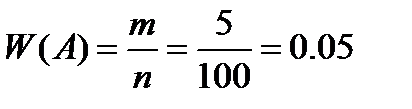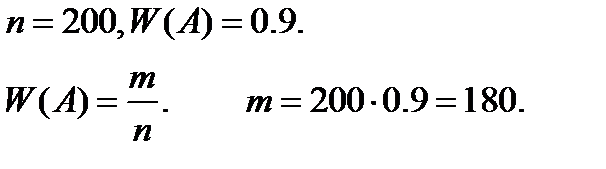|
|
Иов Борецкий – митрополит – МилостынеюМатематика вивчає закономірні явища матеріального світу. Закономірні події – це події, які завжди відбуваються при однакових умовах. Поряд з закономірними спостерігаються незакономірні – випадкові, які не передбачувані. Випадкова подія – це подія, що може відбутися або не відбутися внаслідок випробування ( досліду, стохастичного експерименту), результат якої наперед не можна передбачити. Нехай в серіях в Виявляється, що в серіях великого масового числа випробувань відносна частота Кожен результат події називається елементарною подією. Довільна підмножина елементарних подій – називається випадковою подією. Елементарні події бувають: вірогідні, неможливі, єдино можливі, рівноможливі, несумісні і сумісні. Вірогідна – при випробуванні може здійснитися Неможлива – яка не відбудеться Єдино можлива подія – поява її є вірогідною Рівноможливі – за однакових умов випробування поява однієї не має переваги перед появою іншої. Несумісні (сумісні) – поява однієї виключає (не виключає) появу іншої в одному експерименті Результат або наслідок події: благоприємні або неблагоприємні
Позначимо
Оскільки за означенням випадкова подія є підмножиною простору , як універсальної множини, тому можна використовувати по аналогії означення операції над множинами для означення операції над випадковими подіями, а також діаграми Ейлера-Венна для їх зображення.
Приклад. Монету підкидають тричі. Описати простір елементарних подій та події А – принаймні один раз з'явиться герб, В – за другого підкидання з'явиться цифра. Знайти Розв’язання: елементарні події
Простір елементарних подій:
Події
За означеннями суми, добутку, різниці подій та протилежної події:
ЗАКОНИ ОПЕРАЦІЙ НАД ВИПАДКОВИМИ ПОДІЯМИ
def. Імовірністю події А називається означена на алгебрі подій простору
ПОВНА ГРУПА ПОДІЙ
КЛАСИЧНЕ ОЗНАЧЕННЯ ЙМОВІРНОСТІ
ГЕОМЕТРИЧНА ЙМОВІРНІСТЬ
СТАТИСТИЧНА ЙМОВІРНІСТЬ У випадках, коли для обчислення ймовірності випадкової події неможливо побудувати її імовірнісну модель простору елементарних подій, які за певного числа проведених експериментів в однакових умовах характеризуються стійкістю відносних частот. В таблиці наведено результати дослідів, що проводились французьким природознавцем Ж. Бюффоном (Georges Louis Lecrerc Comte de Buffon, 1707-1788) і англійським математиком К. Пірсоном (Carl Pearson, 1857-1936). Відносна частота мало відхиляється від 0.5.
Означення. Статистичною ймовірністю статистично стійкої випадкової події А називається її відносна частота і позначається
де m – число експериментів, в яких подія А відбулася, n – загальне число всіх проведених експериментів. Приклад. У випробуванні відносна частота стандартних деталей із 300 деталей дорівнює 0,85. Знайти число стандартних деталей.
Схема урн: вибірка проводиться з урни, в якій ретельно перемішані різнокольорові кулі одного радіуса гладкої поверхні однієї ваги. Елементарні події за схемою урн наз. рівноймовірними, якщо ймовірності їх настання однакові. Приклади 1.В урні: 15 ч.,9 с.,6 з. куль. Навмання виймають 6 куль. Яка ймовірність того, що серед вийнятих куль буде 3 ч.,2 с.,1 з? Розв’язання:
2.Із карток з літерами А,Б,В,К,І,Н,О,П,Р,Ш вибирають 6. Яка йм. складання слова БАНКІР?
3.У цеху 15 верстатів, які знаходяться або в робочому стані або ні. Знайти ймовірність того, що під час роботи вийдуть з ладу 4 верстати.
4.Монета підкидається 20 разів. Знайти йм. того, що орел випаде 7 або (+) 17 разів.
5. (Геометрична ймовірність) Знайти ймовірність того, що числа
6.(Статистична ймовірність) З партії деталей вибрано 100, серед яких виявилося 5 бракованих. Знайти відносну частоту появи брак. дет.
7.Відносна частота станд. дет із 200 дет. дорівнює 0.9. Знайти число станд.дет.
|
|
 незалежних випробувань випадкова подія настане
незалежних випробувань випадкова подія настане  раз. Число
раз. Число 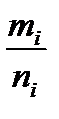 - відносною частотою настання випадкової події в серіях з
- відносною частотою настання випадкової події в серіях з  , і з деякою похибкою коливається в околі деякого сталого числа р, яке об’єктивно є її числовою характеристикою. Теорія ймовірностей вивчає закономірності випадкових подій, для яких властива стійкість відносної частоти при масових випробуваннях.
, і з деякою похибкою коливається в околі деякого сталого числа р, яке об’єктивно є її числовою характеристикою. Теорія ймовірностей вивчає закономірності випадкових подій, для яких властива стійкість відносної частоти при масових випробуваннях. - множина всіх можливих результатів події в серії випробувань. Кожний результат події будемо називати елементарною подією, що позначається
- множина всіх можливих результатів події в серії випробувань. Кожний результат події будемо називати елементарною подією, що позначається  . Люба підмножина множини
. Люба підмножина множини  елементарних подій називається простором елементарних подій і на ній означені операції суми, добутку, доповнення, т.б. визначена алгебра випадкових подій.
елементарних подій називається простором елементарних подій і на ній означені операції суми, добутку, доповнення, т.б. визначена алгебра випадкових подій.



 подія А спричиняє подію В
подія А спричиняє подію В

 відбулася хоча б одна з подій
відбулася хоча б одна з подій

 відбуваються події А і В
відбуваються події А і В
 подія А відбулася, а В – ні
подія А відбулася, а В – ні

 події несумісні
події несумісні

 обидві настають або ні
обидві настають або ні
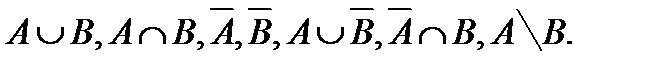
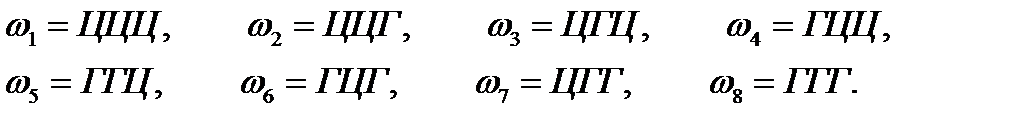
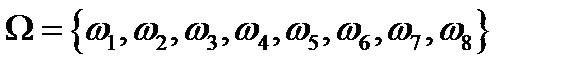
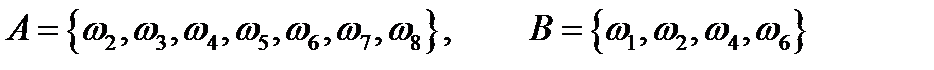
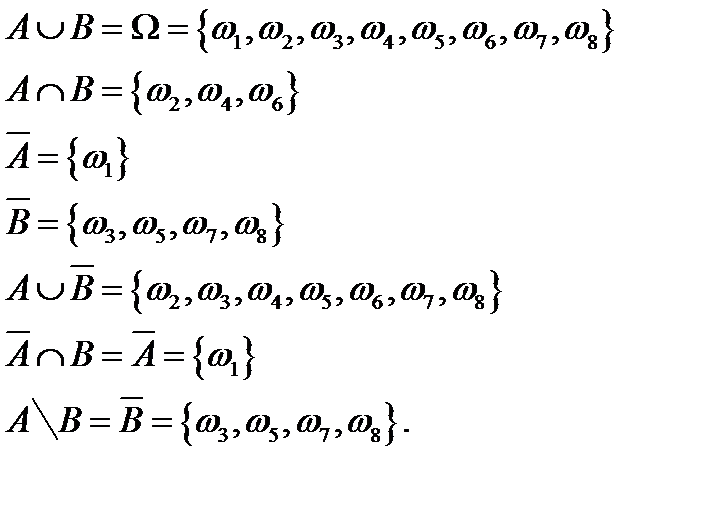
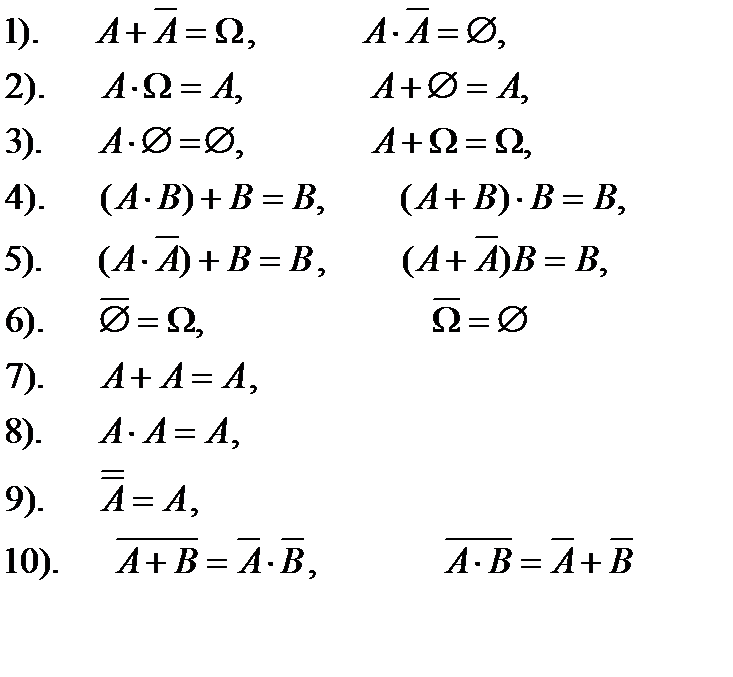
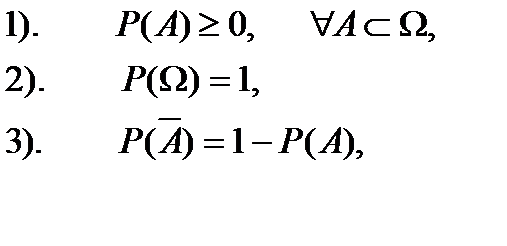
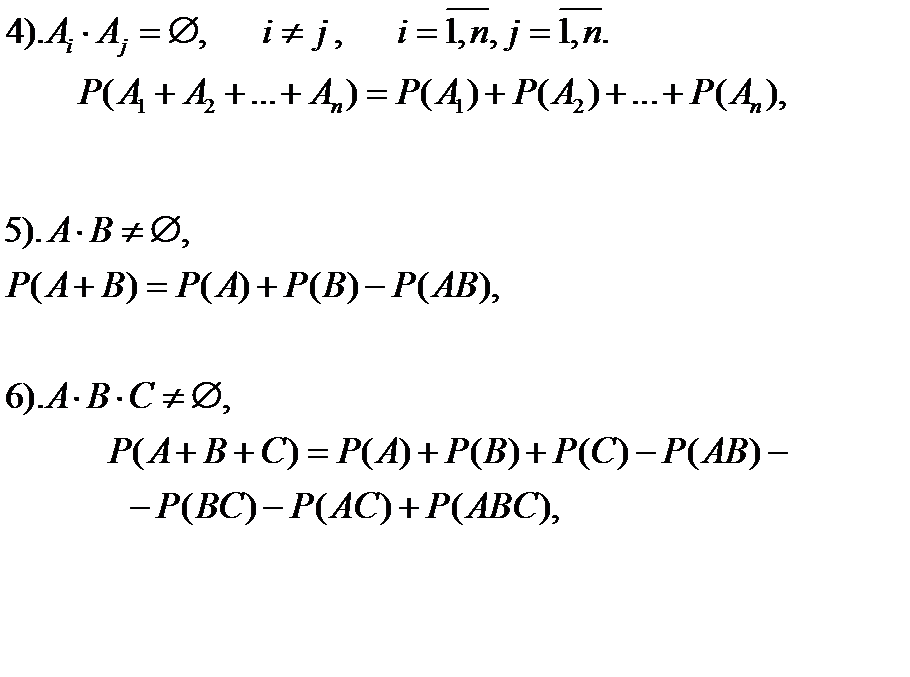

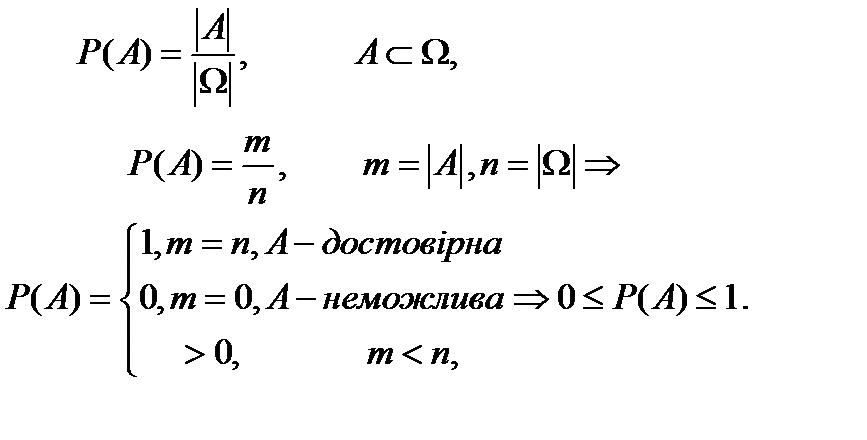
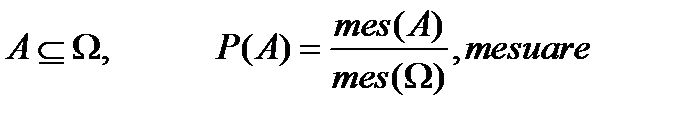
 )
)
 ,
, .
.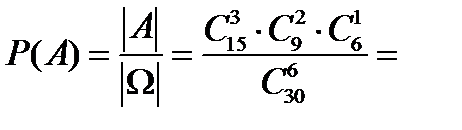
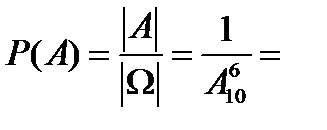
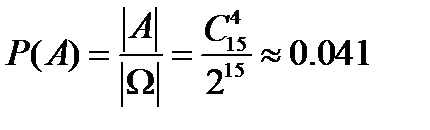
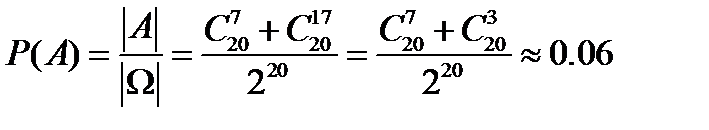
 задовольняють нерівності
задовольняють нерівності