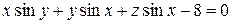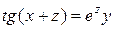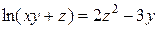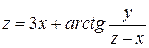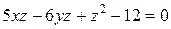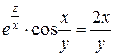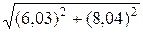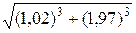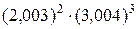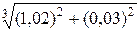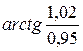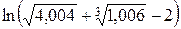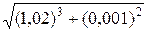|
|
Найти общее решение уравненияУЧЕБНЫЕ МАТЕРИАЛЫ для студентов заочной формы обучения
по дисциплине Математика
для направления подготовки 38.03.03 (080400.62) Управление персоналом по профилю -Рекрутмент; - Управление профессиональным развитием персонала; - Документационное обеспечение и учет персонала.
Общая трудоемкость дисциплины 360 часов, 10 з.е.
Краткое содержание курса 1. линейная алгебра 2. аналитическая геометрия 3. векторный анализ; 4. последовательности и ряды; 5. функции и множества; 6. дифференциальное исчисление 7. интегральное исчисление; 8. дифференциальные уравнения; 9. теория вероятности; 10. математическая статистика. 11. линейное программирование . Форма текущего контроля Формой текущего контроля является контрольная работа. При выполнении контрольных работ студент должен руководствоваться следующими указаниями: 1) каждая работа должна выполняться в отдельной тетради (в клетку), на внешней обложке которой должны быть ясно написаны фамилия студента, его инициалы, номер контрольной работы; 2) контрольные задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением каждой задачи надо полностью переписать ее условия; 3) решение задач следует излагать подробно, делая соответствующие ссылки на вопросы теории с указанием необходимых формул, теорем; 4) решение задач геометрического содержания должно сопровождаться чертежами, выполненными аккуратно, с указанием осей координат и единиц масштаба. Объяснения к задачам должны соответствовать обозначениям, приведенным на чертежах; 5) на каждой странице тетради необходимо оставлять поля шириной 3 – 4 см для замечаний преподавателя; 6) контрольные работы должны выполняться самостоятельно. Не самостоятельно выполненная работа лишает студента возможности проверить степень своей подготовленности по теме. Если преподаватель установит несамостоятельное выполнение работы, то она не будет зачтена. 7) Контрольная работа №1 выполняется в первом семестре, контрольная №2 – во втором и контрольная №3 – в третьем. 8) Номер варианта контрольной работы выбирается студентом по первой букве фамилии студента. 9) Не позднее чем за неделю до сессии работа должна быть сдана на кафедру.
*** Задания для контрольной работы Контрольная работа № 1 1.Элементы линейной алгебры 1 – 10. Дана система линейных уравнений Доказать ее совместность и решить тремя способами: 1) методом Гаусса; 2) метод Крамера; 3) средствами матричного исчисления.
2.Элементы векторной алгебры 11 – 20. Даны координаты вершин пирамиды 11. 12. 13. 14. 15. 16. 17. 18. 19. 20.
3. Аналитическая геометрия на плоскости 21. В треугольнике ABC даны: уравнение стороны AB: 22. Даны две вершины 23. Дано уравнение одной из сторон квадрата 24. Составить уравнения сторон треугольника, зная одну его вершину B(2; 6), а также уравнения высоты 25. Точка A(5; -1) является вершиной квадрата, одна из его сторон лежит на прямой 26. Даны две противоположные вершины квадрата A(3; 0) и C(-4; 1). Найти координаты двух его других вершин. 27. Даны уравнения боковых сторон равнобедренного треугольника 28. Две противоположные вершины квадрата находятся в точках A(3; 5) и B(1; -3). Найти его площадь. 29. Даны уравнения двух сторон треугольника и 30. Составить уравнения сторон треугольника, если дана одна его вершина
4. Аналитическая геометрия в пространстве 31. Составить уравнение плоскости проходящей через точку 32. Составить уравнение плоскости, которая проходит через две точки 33. Даны вершины треугольника 34. Составить уравнение прямой, которая проходит через точку и пересекает прямую и пересекает прямую М(-1;2;-3)перпендикулярно к вектору 35. Составить уравнение прямой, проходящей через точку L(2;-3;-5)перпендикулярно к плоскости 36. Составить уравнение плоскости, проходящей через прямую 37. Составить уравнение плоскости, проходящей через две параллельные прямые 38. Составить уравнение плоскости, проходящей через точку пересечения плоскостей 39. Дана плоскость 40. Найти координаты точки пересечения прямой
5. Полярная система координат 41 – 50.Линия задана уравнением
6. Введение в математический анализ 51 – 60. Найти область определения функции.
61 – 70. Построить графики функций при помощи преобразований графиков основных элементарных функций.
71 – 80. Найти пределы функций не пользуясь правилом Лопиталя.
81 – 90. Задана функция y=f(x)и два значения аргумента
91 – 100. Задана функция y=f(x). Найти точки разрыва, если они существуют. Сделать чертеж.
Контрольная работа № 2 1-10Вычислить производную 1.а) в) д) 2.а) в) д)
3.а) в) д) 4. а) в) д) 5. а) в) д) 6.а) в) y= д) 7.а) в) д) 8.а) в) д) 9.а) в) д) 10. а) в) д)
11-20Построить график функции с помощью дифференциального исчисления. 11. а) 12. а) 13. а) 14. а) 15. а) 16. а) 17. а) 18. а) 19. а) 20.а) 21-30 Найти наибольшее и наименьшее значение функции на отрезке 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
31-40Вычислить неопределенный интеграл 31. в)
32.a) в)
33.a) в) 34.a) в) 35.a) в) 36.a) в)
37.a) в) 38.a) в) 39.a) в) 40.a) в) 41-50Вычислить определенный интеграл 41. а) 42. а) 443. а) 44. а) 45. а) 46. а) 47. а) 48. а) 49. а) 50. а)
Найти общее решение уравнения
71-80Найти область определения функции двух переменных (дать геометрическое истолкование). 71. 72. 73. 74. 75. 76. 77. 78. 79. 80.
81-90Найти частные производные 81. 82. 83. 84. 85. 86. 87. 88. 89. 90. 91-100Найти частные производные 91. 92. 93. 94. 95. 96. 97. 98. 99. 100. 101-110 Вычислить приближенно с помощью полного дифференциала. 101. 102. 103. 104 105. 106. 107. 108. 109. 110. Контрольная работа № 3 Теория вероятностей 1-10 1. Три стрелка выстрелили по зверю, который после этого оказался убитым одной пулей. Определить вероятность того, что зверь был убит каждым охотником, если вероятности попадания для них соответственно равны 0,2;0,4;0,6. 2. Три стрелка произвели залп по цели. Вероятность поражения цели первым стрелком равна 0,7; для второго и третьего стрелков вероятности соответственно равны 0,8 и 0,9. Найти вероятность того, что: а) только один из стрелков поразит цель; б) только два стрелка поразят цель; в) все три стрелка поразят цель; г) хотя бы один из стрелков поразит цель. 3. Вероятность хотя бы одного попадания при двух выстрелах равна 0,96. Найти вероятность трех попаданий при четырех выстрелах. 12 |
|







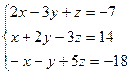
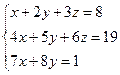


 . Найти: 1) угол между ребрами
. Найти: 1) угол между ребрами  и
и  ; 2) угол между ребром
; 2) угол между ребром  и гранью
и гранью  ; 3) площадь грани
; 3) площадь грани  на грань
на грань 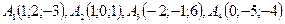
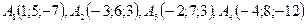
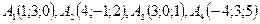
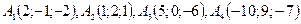





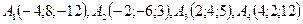
 , уравнения высот AM:
, уравнения высот AM: 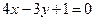 и BN:
и BN:  . Составить уравнения двух других сторон и третьей высоты этого треугольника.
. Составить уравнения двух других сторон и третьей высоты этого треугольника. и
и  треугольника ABC и точка
треугольника ABC и точка 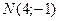 пересечения его высот. Составить уравнения сторон треугольника.
пересечения его высот. Составить уравнения сторон треугольника. и точка пересечения его диагоналей
и точка пересечения его диагоналей  . Найти уравнения трех остальных сторон квадрата.
. Найти уравнения трех остальных сторон квадрата. и биссектрисы
и биссектрисы 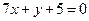 , проведенных из одной вершины.
, проведенных из одной вершины.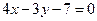 . Составить уравнения других сторон квадрата.
. Составить уравнения других сторон квадрата. и
и  и точка (5;0) на его основании. Найти периметр и площадь треугольника.
и точка (5;0) на его основании. Найти периметр и площадь треугольника.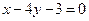 . Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке
. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке  .
.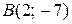 , а также уравнения высоты
, а также уравнения высоты  и медианы
и медианы 
 , проведенных из разных вершин.
, проведенных из разных вершин. параллельно плоскости
параллельно плоскости  .
. и
и  перпендикулярно к плоскости
перпендикулярно к плоскости  .
. ,
,  и
и  . Составить параметрическое уравнение его медианы, проведенной из вершины C.
. Составить параметрическое уравнение его медианы, проведенной из вершины C. и пересекает прямую
и пересекает прямую  .
.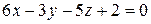 .
. и точку A(2;-2;1).
и точку A(2;-2;1). ,
,  .
. 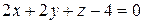 ,
,  ,
,  и через точки М(0;3;0) и N(1;1;1).
и через точки М(0;3;0) и N(1;1;1). и вне ее точка М(1;1;1). Найти точку N, симметричную точке М относительно данной плоскости.
и вне ее точка М(1;1;1). Найти точку N, симметричную точке М относительно данной плоскости. с плоскостью
с плоскостью  .
. в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от
в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от  до
до  и придавая
и придавая 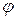 значения через промежуток
значения через промежуток  ; 2) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
; 2) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия.






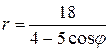


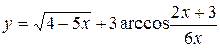 б)
б) 
 б)
б) 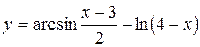
 б)
б) 
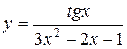 б)
б) 
 б)
б) 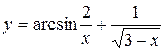
 б)
б) 
 б)
б) 

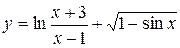 б)
б) 
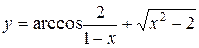 б)
б) 
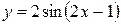

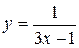
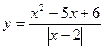


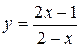











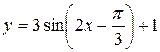





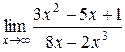
















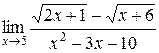






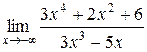


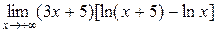
 )
)
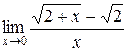
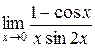





 и
и 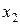 . Требуется установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента, в случае разрыва функции найти ее пределы слева и справа.
. Требуется установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента, в случае разрыва функции найти ее пределы слева и справа.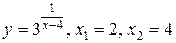 ,
,



















 б)
б) 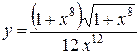
 г)
г) 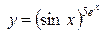
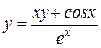
 б)
б) 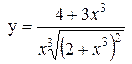
 г)
г) 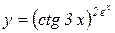
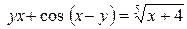
 б)
б) 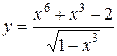
 г)
г) 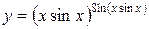
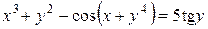
 б)
б) 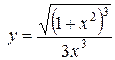
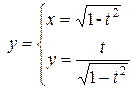 г)
г)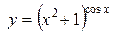
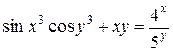
 б)
б) 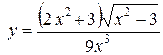
 г)
г)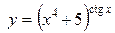
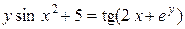

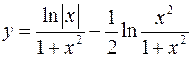 б)
б) 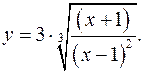
 г)
г) 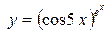
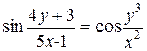
 б)
б)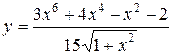
 г)
г) 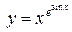
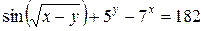
 б)
б)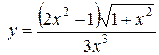
 г)
г)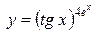
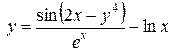
 б)
б) 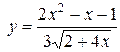
 г)
г) 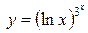
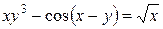
 б)
б) 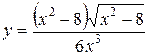
 г)
г) 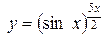
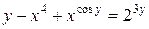
 б)
б) 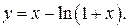
 б)
б) 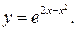
 б)
б) 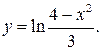
 б)
б) 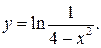
 б)
б) 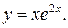
 б)
б) 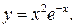
 б)
б) 
 б)
б) 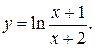
 б)
б) 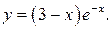
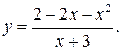 б)
б) 
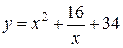


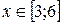
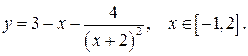
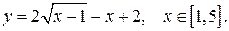
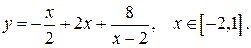
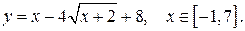
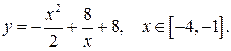
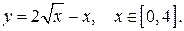
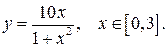
 б)
б) 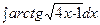
 г)
г) 
 б)
б) 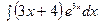
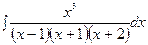 г)
г)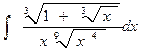
 б)
б) 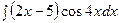
 г)
г)
 б)
б) 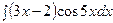
 г)
г) 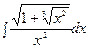

 б)
б) 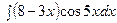
 г)
г)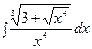
 б)
б) 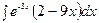
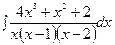 г)
г)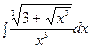
 б)
б)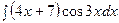
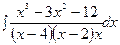 г)
г)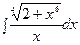
 б)
б)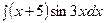
 . г)
. г)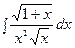
 б)
б)
 г)
г)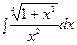
 б)
б)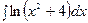
 г)
г) 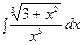
 б)
б) 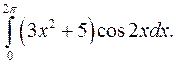
 б)
б) 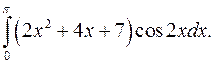
 б)
б) 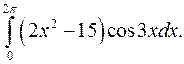
 б)
б) 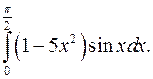
 б)
б) 
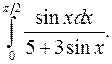 б)
б) 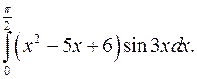
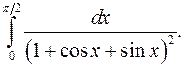 б)
б) 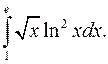
 б)
б) 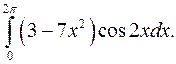
 б)
б) 
 б)
б) 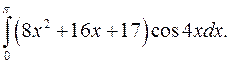







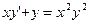






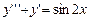
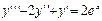


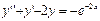

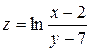
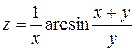

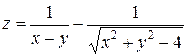
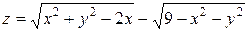
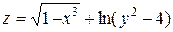


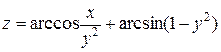
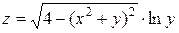
 ,
,  от функции
от функции  .
.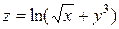
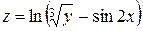
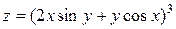
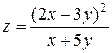
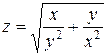
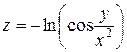
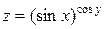
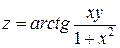
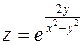

 ,
,  от неявной функции
от неявной функции