|
|
Завдання до лабораторної роботиМЕТОДИЧНІ ВКАЗІВКИ
до виконання лабораторних робіт студентів з дисципліни “ТЕОРІЯ АЛГОРИТМІВ” для студентів I курсу денної форми навчання Напрям підготовки – комп’ютерні науки
Одеса 2014
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ ОДЕСЬКИЙ ДЕРЖАВНИЙ ЕКОЛОГІЧНИЙ УНІВЕРСИТЕТ Затверджено Проректор з методичної роботи ______________Хохлов В.М. МЕТОДИЧНІ ВКАЗІВКИ
до виконання лабораторних робіт студентів з дисципліни “Теорія алгоритмів” для студентів I курсу денної форми навчання Напрям підготовки – комп’ютерні науки
Затверджено на засіданні кафедри інформаційних технологій протокол №________ від "___"____________ 2014 р. Завідувач кафедри ______________ Препелиця Г.П. Затверджено на засіданні методичної комісії факультету протокол № _________ від “___”_____________2014р. Декан факультету КН _______________Коваленко Л.Б.
Одеса 2014 Методичні вказівки до виконання лабораторних робіт студентів з дисципліни “Теорія алгоритмів”, для студентів I курсу денної форми навчання. Напрям підготовки – комп’ютерні науки / Укладачі: Шпінарева І.М.., к.ф.м.н, доц.– Одеса, ОДЕКУ, 2014. - 53 с.
ЗМІСТ
Передмова. 5 Список літератури. 7 Лабораторна робота № 1.1 «Аналіз алгоритмів та алгоритмічні стратегії». 8 Лабораторна робота № 1.2 «Прості та покращені алгоритми сортування». 17 Лабораторна робота № 2 «Рекурсия. Список». 27 Лабораторна робота № 3 «Рекурсія . Задача пошуку. Лінійний та бінарний пошук» 33 Лабораторна робота № 4 «Реалізація пошуку з використанням хеш-таблиць» 41 Індивідуальне завдання «Фундаментальні алгоритми на графах і деревах». 47 ДОДАТОК А Програмний код двійкового дерева пошуку. 60 ДОДАТОК В Хеш-таблиця. 67 Передмова Методичні вказівки призначені для студентів I курсу денної форми навчання. Мета виконання лабораторних робіт – закріплення теоретичного лекційного матеріалу та придбання практичних навичок програмування мовою Javа базових алгоритмів та їх подальше застосування для вирішенні різних задач, засвоєння основних результатів та методів теорії алгоритмів, теорії рекурсивних функцій та теорії складності обчислень. Дисципліна «Теорії алгоритмів» є нормативною дисципліною у напрямі бакалаврської підготовки «Комп’ютерні науки». Внаслідок вивчення даної дисципліни студенти повинні знати основні відомості з аналізу алгоритмів і алгоритмічних стратегій та фундаментальні алгоритми (алгоритми сортування, злиття та пошуку, комбінаторні алгоритми, рекурсивні алгоритми,і алгоритми на графах і деревах). Вони повинні вмітизастосовувати алгоритми сортування, злиття та пошуку, комбінаторні алгоритми, рекурсивні алгоритми та алгоритми на графах і деревах та програмування алгоритмів мовою Java. Методичні вказівки містять рекомендації по вивченню розділів дисципліни, контрольні запитання та завдання. Всі лабораторні роботи підкріплені прикладами розв’язання типових задач на ПЕОМ. Під час підготовки до лабораторної роботи студент повинен вивчити відповідний теоретичний матеріал за конспектом лекцій і літературою, що рекомендована викладачем, розібрати приклади розв’язання задач, наведених у даних методичних вказівках, а також відповісти на контрольні питання. Кожна лабораторна робота містить перелік тем, які повинні бути розглянуті та знання, які є необхідними для рішення поставленої задачі. Виконанню лабораторної роботи передує практичне заняття з відповідної теми. На практичних заняттях розглядаються алгоритми рішення задач для того, щоб під час лабораторної роботи студенти складали програму, користуючись розглянутими алгоритмами. На початку лабораторної роботи викладач проводить співбесіду за результатами якої студент отримує, або не отримує допуск до виконання лабораторної роботи. Якщо студент не отримав допуску, він залишається на заняттях, але не виконує лабораторної роботи на комп’ютері. Замість цього він вивчає теоретичний матеріал за даною темою, щоб відповісти на питання викладача та отримати допуск до виконання роботи. За кожну лабораторну роботу студент отримує оцінки: за виконання та за захист роботи. Максимальні бали з кожної лабораторної роботи встановлюються ведучим викладачем. На першому занятті студенти отримують графік контролюючих заходів з дисципліни: перелік контролюючих заходів, терміни виконання, бали за кожний вид робіт.
Список літератури 1. Б.Н.Иванов, Дискретная математика. Алгоритмы и программы. Москва, 2001. 2. Уоррен Г. (H.Warren) Алгоритмические трюки для программистов, М.: Издательский дом "Вильямс", 2003. - 288 с.: ил. 3. Котов В.М., Волков И.А., Лапо А.И., Информатика. Методы алгоритмизации., Мн.; 2000. - 300с.: ил. 4. Окулов С.М., Программирование в алгоритмах ̶ М.: БИНОМ. Лаборатория знаний, 2002. ̶ 341 с: ил. 5. Глушаков С.В. Программирование на Java 2: Изд.2-е.- Харьков: Фолио, 2003. – 536 с. – (Учебный курс). 6. А.В. Картузов, Д.В. Николенко. Программируем на языке Java – СПб: Наука и техника, 2001. – 192 стр. с ил. 7. Любош Бруга. Java по-быстрому. Практический экспресс-курс – СПб: Наука и техника, 2006. – 384 с. :ил. 8. Аккуратов Е.Е. Знакомьтесь: Java. Самоучитель. – М.: Изд. Дом «Вильямс», 2006. – 256с.: ил. Додаткова 9. Кормен Т., Лейзерсон Ч., Ривест Р.Л., Штайн К. Алгоритмы: построение и анализ, 2-е издание. : Пер. с англ. – М. : Издательский дом «Вильямс», 2005. – 1296 с. 10. Левитин А. В. Алгоритмы: введение в разработку и анализ. : Пер. с англ. – М. : Издательский дом «Вильямс», 2006. – 576 с. 11. Robert Lafore Data Structures & Algorithms in Java Second Edition–2003. –801с. 12. Карпов Ю.Г., Трифонов П.В. Сложность алгоритмов и программ. 13. Сборник "Зимняя школа Харьков 2011". Ресурси мережі Інтернет 14. Теорія алгоритмів. [Електронний ресурс]. – Режим доступу: http://talg.weebly.com/.
Лабораторна робота № 1.1
Тема: «Аналіз алгоритмів та алгоритмічні стратегії»
Мета роботи
Метою лабораторної роботи є отримання практичних навичок визначати часову складність алгоритму. Познайомитися з алгоритмами на НСД, НСК, алгоритм Євклида, алгоритм "Решето Ератосфена". Навчитися будувати алгоритми з мінімальною часовою складністю для вирішення поставлених задач.
Завдання до лабораторної роботи Використовуючи алгоритми, розглянуті на практичному занятті, скласти програму розрахунку заданих величин та провести аналіз ефективності реалізованих алгоритмів. Методичні вказівки Лабораторна робота спирається на знання й уміння, отримані при вивченні наступних тем лекційного курсу: - Поняття алгоритму, властивості. Алгоритмічні системи. - Поняття складності обчислення. Функція складності обчислень (за часом). - Класи складності.Опис класів P і NP. Приклади NP-повних задач. Проблема перебору (P = NP?). Застосування теорії NP-повноти для аналізу складності завдань. Тому під час підготовки до лабораторної роботи рекомендується повторити зазначені розділи дисципліни. Наведемо нижче декілька важливих визначень, які слід пам’ятати під час виконання лабораторної роботи. Основними мірами обчислювальною складності алгоритмів є: - часова складність, яка характеризує час, необхідний для виконання алгоритму на даній машині; цей час, як правило, визначається кількістю операцій, які потрібно виконати для реалізації алгоритму; - ємнісна складність, яка характеризує пам'ять, необхідну для виконання алгоритму. Часова та ємнісна складність тісно пов'язані між собою. Обидві є функціями від розміру вхідних даних. Надалі обмежимося тільки аналізом часової складності. Складність алгоритму описується функцією f(n), де n - розмір вхідних даних. Важливе теоретичне і практичне значення має класифікація алгоритмів, яка бере до увагу швидкість зростання цієї функції. Асимптотичні позначення - «О велике». Цей клас складається з функцій, що ростуть не швидше функції Визначення. Кажуть, що f(n) = O (g(n)), якщо існує така константа с > 0, що для будь-якого n виконується нерівність: |f(n)| <= с |g(n)|. Оскільки і розмір вхідних даних, і кількість операцій є величинами невід'ємними (а фактично - додатними), модулі можна опустити. - «Омега велике». Клас функцій, що ростуть принаймні так само швидко як функція Визначення. Кажуть, що f(n) = - Через Визначення. Кажуть, що f(n) = Виділяють такі основні класи алгоритмів: - логарифмічні: f(n) = O (log2n); - лінійні: f(n) = O (n); - поліноміальні: f(n) = O (nm); тут m ̶ натуральне число, більше від одиниці; при m = 1 алгоритм є лінійним; - експоненційні: f(n) = O (an); a ̶ натуральне число, більше від одиниці. Для однієї й тієї ж задачі можуть існувати алгоритми різної складності.
Приклади аналізу алгоритмів
Проаналізуємо декілька простих алгоритмів, на основі яких розглянемо усі важливі етапи, які зазвичай виконуються при аналізі подібних алгоритмів. Приклад 1. Розглянемо задачу пошуку найбільшого елементу в списку з
Алгоритм MaxElement // Вхідні дані: масив дійсних чисел // Вихідні дані: повертається значення найбільшого елементу масиву A
Очевидно, що в цьому алгоритмі розмір вхідних даних треба оцінювати по кількості елементів в масиві, тобто числом Позначимо через
Приклад 2. Розглянемо задачу знаходження максимального елемента в матриці Цю задачу можна вирішити за допомогою приведеного нижче нескладного алгоритму. Алгоритм MaxElements // Вхідні дані: масив дійсних чисел // Вихідні дані: повертається значення max Max=A[0][0];
У цьому алгоритмі, як і у попередньому, розмір вхідних даних цілком природно оцінювати по кількості елементів у масиві, тобто числом Позначимо через Таким чином, отримаємо:
Задача знаходження максимального елемента в матриці має складність О(n2).
Приклад 3. Розглянемо задачу перевірки єдиності елементів. Іншими словами, треба переконатися, що усі елементи масиву різні. Цю задачу можна вирішити за допомогою приведеного нижче нескладного алгоритму. Алгоритм Elements // Вхідні дані: масив дійсних чисел // Вихідні дані: повертається значення true, якщо усі елементи масиву // різні, та falseу іншому випадку. boolean l=true;
У цьому алгоритмі, як і у попередньому, розмір вхідних даних цілком природно оцінювати по кількості елементів у масиві, тобто числом За визначенням найгірший випадок вхідних даних відповідає такому масиву елементів, при обробці якого кількість операцій порівнянь
Зверніть увагу, що цей результат можна було легко передбачити: у розглянутому алгоритмі у найгіршому випадку для масиву, який складається з Приклад 4. Розглянемо алгоритм Решето Ератосфена. Решето Ератосфена ̶ це алгоритм знаходження простих чисел до заданого числа n. У процесі виконання даного алгоритму поступово відсіваються складені числа, кратні простим, починаючи з 2. Цю задачу можна вирішити за допомогою приведеного нижче нескладного алгоритму.
Оцінимо складність алгоритму. Перше викреслення вимагає n / 2 дій, друге ̶ n / 3, третє ̶ n / 5 і т. д. За формулою Мертенса
Так що для решета Ератосфена буде потрібно O (n log log n) операцій. Споживання пам'яті ж складе O (n). План аналізу ефективності алгоритмів: 1. оберіть параметр (чи параметри), по якому буде оцінюватися розмір вхідних даних алгоритму; 2. визначите основну операцію алгоритму (як правило, вона знаходиться в найглибше вкладеному внутрішньому циклі алгоритму); 3. перевірте, чи залежить кількість виконуваних операцій тільки від розміру вхідних даних. Якщо воно залежить і від інших чинників, розгляньте при необхідності, як змінюється ефективність алгоритму для найгіршого, середнього та найкращого випадків; 4. запишіть суму, що виражає кількість виконуваних основних операцій алгоритму; 5. використовуючи стандартні формули і правила підсумовування, спростіть отриману формулу для кількості основних операцій алгоритму. Якщо це неможливо, визначте хоча б порядок зростання.
Контрольні питання
1. У чому полягає задача аналізу алгоритмів? 2. Які два види ефективності розглядаються у даному курсі? 3. У чому вимірюється час роботи алгоритму? 4. Як відбувається оцінка вхідних даних? 5. Які існують випадки вхідних даних? 6. Що таке порядок зростання алгоритмів? Які класи зростання ви знаєте? 7. У чому полягає асимптотичний аналіз алгоритмів? 8. Які асимптотичні позначення ви знаєте?
Завдання до лабораторної роботи
1. Побудувати алгоритм множення двох натуральних чисел без використання операції множення. 2. Побудувати алгоритм знаходження n-го простого числа. 3. Побудувати алгоритм знаходження біноміального коефіцієнта Cn k для цілих n та k, де 0≤k≤n . Використайте наступні співвідношення: Cn 0=Cn n=1,Cn+1 k+1=Cn .k+1.+Cn k. 4. Побудувати алгоритм знаходження всіх натуральних розв'язків нерівності x2+y2.<n для заданого натурального числа n. 5. Побудувати алгоритм, який для введеного цілого числа R знайде кількість точок з цілочисельними координатами, які лежать всередині кулі з радіусом R і центром в початку координат. 6. Побудувати алгоритм, який для заданого цілого числа x шукатиме найбільш близикий до √x дріб n/m , де m<100 . 7. Побудувати алгоритм для знаходження кількості щасливих білетів із шестизначними номерами. Білет вважається щасливим, якщо сума перших трьох цифр дорівнює сумі трьох останніх. 8. Побудувати алгоритм знаходження суми 1/0!+ 1/1!+ 1/2!+..... +1/n! , складність якого була б лінійною. 9. Є 25 золотих монет. Всі вони мають однакову вагу, за винятком однієї монети з дефектом, яка важить менше інших. Розробіть алгоритм, що визначає дефект за три зважування. Яка максимальна кількість монет, для яких можна визначити монету з дефектом не більш ніж за три зважування на вагах з чашками? 10. Три місіонери і три канібали знаходяться на одному березі річки; човен може перевезти двох чоловік. Всі вони хочуть перебратися через річку. Не можна допустити, щоб на одному березі знаходилася група місіонерів з численнішою групою канібалів. Розробіть процедуру, що дозволяє всім шістьом перебратися через річку. 11. Побудувати алгоритм, який здійснює обхід шахівниці конем. При чому кінь ніколи не буває двічі на одній клітці. 12. Побудувати алгоритм знаходження найбільшої спільної підпослідовності двох послідовностей. 13. Побудувати алгоритм, який набиратиме суму N копійок з набору монет 1, 2, 5,10, 25 та 50 копійок.
|
|
 .
. .
. (g(n)), якщо існує така константа с > 0, що для будь-якого n виконується нерівність: f(n) ≥ с g(n).
(g(n)), якщо існує така константа с > 0, що для будь-якого n виконується нерівність: f(n) ≥ с g(n). («тета велике») ми позначаємо клас функцій, що ростуть з тією ж швидкістю що і функція
(«тета велике») ми позначаємо клас функцій, що ростуть з тією ж швидкістю що і функція  (g(n)), якщо існує такі константи с1 > 0, с2>0, що для будь-якого n виконується нерівність: с1 g(n)≤ f(n) ≤с2 g(n).
(g(n)), якщо існує такі константи с1 > 0, с2>0, що для будь-якого n виконується нерівність: с1 g(n)≤ f(n) ≤с2 g(n). чисел. Для простоти припустимо, що цей список реалізований у вигляді масиву. Нижче приведений псевдокод алгоритму.
чисел. Для простоти припустимо, що цей список реалізований у вигляді масиву. Нижче приведений псевдокод алгоритму.


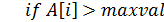


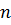 . Операції, що виконуються найчастіше, знаходяться у внутрішньому циклі
. Операції, що виконуються найчастіше, знаходяться у внутрішньому циклі  алгоритму. Таких операцій дві: порівняння
алгоритму. Таких операцій дві: порівняння  та привласнення
та привласнення  . Яку з них вважати базовою? Оскільки порівняння виконується на кожному кроці циклу, а привласнення – ні, логічно вважати, що основною операцією алгоритму є операція привласнення. (Зверніть увагу, що для будь-якого масиву розміром n кількість операцій порівняння в даному алгоритмі постійна. Тому не требо окремо розглядати ефективність алгоритму для гіршого, середнього і кращого випадків).
. Яку з них вважати базовою? Оскільки порівняння виконується на кожному кроці циклу, а привласнення – ні, логічно вважати, що основною операцією алгоритму є операція привласнення. (Зверніть увагу, що для будь-якого масиву розміром n кількість операцій порівняння в даному алгоритмі постійна. Тому не требо окремо розглядати ефективність алгоритму для гіршого, середнього і кращого випадків). кількість виконуваних в алгоритмів операцій порівняння та спробуємо вивести формулу, що виражає їх залежність від розміру вхідних даних
кількість виконуваних в алгоритмів операцій порівняння та спробуємо вивести формулу, що виражає їх залежність від розміру вхідних даних  , яке змінюється від 1 до
, яке змінюється від 1 до  включно. Тому для
включно. Тому для 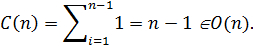
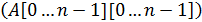

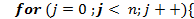

 ;}
;} . Оскільки в найглибше вкладеному внутрішньому циклі алгоритму виконується тільки одна операція порівняння двох елементів, її і вважатимемо основною операцією цього алгоритму.
. Оскільки в найглибше вкладеному внутрішньому циклі алгоритму виконується тільки одна операція порівняння двох елементів, її і вважатимемо основною операцією цього алгоритму. кількість виконуваних в алгоритмів операцій порівняння та спробуємо вивести формулу, що виражає їх залежність від розміру вхідних даних
кількість виконуваних в алгоритмів операцій порівняння та спробуємо вивести формулу, що виражає їх залежність від розміру вхідних даних 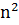 . Змінна зовнішнього циклу
. Змінна зовнішнього циклу 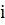 послідовно приймає значення від
послідовно приймає значення від  до
до  . При цьому змінна циклу
. При цьому змінна циклу  послідовно набуває значень від
послідовно набуває значень від 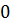 до
до 

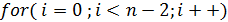 {
{ {
{ l=false;}}
l=false;}}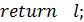
 буде максимальною серед усієї сукупності вхідних масивів розміром
буде максимальною серед усієї сукупності вхідних масивів розміром  послідовно набуває значень від
послідовно набуває значень від  до
до 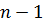 . Внутрішній цикл кожного разу повторюється наново при кожному виконанні зовнішнього циклу. При цьому змінна зовнішнього циклу
. Внутрішній цикл кожного разу повторюється наново при кожному виконанні зовнішнього циклу. При цьому змінна зовнішнього циклу  послідовно приймає значення від
послідовно приймає значення від  до
до  . Таким чином, отримаємо:
. Таким чином, отримаємо:


 різних пар елементів.
різних пар елементів. .
.