|
|
Динамические структуры. Односвязанный списокРассмотрим реализацию простого связанного списка
Список поддерживает следующие операции: · Вставка элемента в начале списка · Удаление элемента в начале списка · Перебор списка для вывода содержимого
Класс Link- предназначен для хранения данных. Класс описывает узел списка
Полное определение класса Link выглядит так: import java.io.*;
//////////////////////////////////////////////////////////////// class Link { public int iData; // data item (key) public double dData; // data item public Link next; // next link in list // ------------------------------------------------------------- public Link(int id, double dd) // constructor { iData = id; // initialize data dData = dd; // (‘next’ is automatically } // set to null) // ------------------------------------------------------------- public void displayLink() // display ourself { System.out.print(“{“ + iData + “, “ + dData + “} “); } } // end class Link ////////////////////////////////////////////////////////////////
В классе LinkList описаны методы для работы со списком:
class LinkList {//указатель на 1 элемент private Link first; // ref to first link on list // ------------------------------------------------------------- public LinkList() // constructor { first = null; // no items on list yet } // ------------------------------------------------------------- //проверка. Является ли список пустым public boolean isEmpty() // true if list is empty { return (first==null); } // ------------------------------------------------------------- // insert at start of list // вставить в начало списка public void insertFirst(int id, double dd) { // make new link Link newLink = new Link(id, dd); newLink.next = first; // newLink --> old first first = newLink; // first --> newLink } // ------------------------------------------------------------- public Link deleteFirst() // delete first item { // (assumes list not empty) Link temp = first; // save reference to link first = first.next; // delete it: first-->old next return temp; // return deleted link } // ------------------------------------------------------------- public void displayList() { System.out.print(“List (first-->last): “); Link current = first; // start at beginning of list while(current != null) // until end of list, { current.displayLink(); // print data current = current.next; // move to next link } System.out.println(“”); } // ------------------------------------------------------------- } // end class LinkList //////////////////////////////////////////////////////////////// Основная программа
class LinkListApp { public static void main(String[] args) { LinkList theList = new LinkList(); // make new list theList.insertFirst(22, 2.99); // insert four items theList.insertFirst(44, 4.99); theList.insertFirst(66, 6.99); theList.insertFirst(88, 8.99); theList.displayList(); // display list while( !theList.isEmpty() ) // until it’s empty, { Link aLink = theList.deleteFirst(); // delete link System.out.print(“Deleted “); // display it aLink.displayLink(); System.out.println(“”); } theList.displayList(); // display list } // end main() } // end class LinkListApp ////////////////////////////////////////////////////////////////
Следующий пример программы добавляет методы : · метод для поиска в связанном списке элемента с указанным значением ключа ; · метод удаление элемента с указанным значением ключа. class LinkList { private Link first; // ref to first link on list // ------------------------------------------------------------- public LinkList() // constructor { first = null; // no links on list yet } // ------------------------------------------------------------- public void insertFirst(int id, double dd) { // make new link Link newLink = new Link(id, dd); newLink.next = first; // it points to old first link first = newLink; // now first points to this } // ------------------------------------------------------------- Public Link find(int key) // find link with given key { // (assumes non-empty list) Link current = first; // start at ‘first’ while(current.iData != key) // while no match, { if(current.next == null) // if end of list, return null; // didn’t find it else // not end of list, current = current.next; // go to next link } return current; // found it } // ------------------------------------------------------------- Public Link delete(int key) // delete link with given key { // (assumes non-empty list) Link current = first; // search for link Link previous = first; while(current.iData != key) { if(current.next == null) return null; // didn’t find it else { previous = current; // go to next link current = current.next; } } // found it if(current == first) // if first link, first = first.next; // change first else // otherwise, previous.next = current.next; // bypass it return current; } // ------------------------------------------------------------- public void displayList() // display the list { System.out.print(“List (first-->last): “); Link current = first; // start at beginning of list while(current != null) // until end of list, { current.displayLink(); // print data current = current.next; // move to next link } System.out.println(“”); } // ------------------------------------------------------------- } // end class LinkList
Лабораторна робота № 3 Тема: «Рекурсія . Задача пошуку. Лінійний та бінарний пошук»
Мета роботи Отримання практичних навичок програмування задач лінійного пошуку у масиві та бінарне дерево пошуку. Вивчення властивості бінарного дерева пошуку. Отримання практичних навичок находження наступного та попереднього елементів бінарного дерева пошуку. Вивчення рекурсивні алгоритми вставки, пошуку та видалення у бінарному дереві пошуку.
Завдання до лабораторної роботи Побудувати бінарне дерево пошуку. І виконати операції : - вставка і видалення елементів; - пошук елемента по ключу; - пошук мінімального елементу; - пошук максимального елементу.
Методичні вказівки
Лабораторна робота спирається на знання й уміння, отримані при вивченні наступних тем лекційного курсу: - Алгоритми лінійного та бінарного пошуку. - Пошук у бінарних деревах. - Рекурсія. Особливості рекурсивних програм. Тому під час підготовки до лабораторної роботи рекомендується повторити зазначені розділи дисципліни. Наведемо нижче декілька важливих визначень, які слід пам’ятати під час виконання лабораторної роботи та перелік важливих методів, що дозволяють полегшити обробку дерева і можуть бути використані при створенні програми лабораторної роботи. У алгоритмах пошуку нас цікавить процес перегляду списку у пошуках деякого конкретного елементу, що називається цільовим. Алгоритм лінійного пошуку послідовно переглядає по одному елементу списку, починаючи з першого, до тих пір, поки не знайде цільовий елемент. Очевидно, що чим далі в списку знаходиться конкретне значення ключа, тим більше часу піде на його пошук. Це слід пам'ятати при аналізі алгоритму. У алгоритмі послідовного пошуку два найгірші випадки. У першому випадку цільовий елемент стоїть в списку останнім. У другому його зовсім немає в списку. Припустимо, що усі ключові значення в списку унікальні, і тому якщо збіг стався в останньому записі, то усі попередні порівняння були невдалими. Проте алгоритм проробляє усі ці порівняння доки не дійде до останнього елементу. В результаті буде виконано Бінарне дерево пошуку– структура даних, яка підтримує багато операцій з динамічними множинами, включаючи пошук елементу, мінімального і максимального значення, попереднього і подальшого елементу, вставку і видалення. Основні операції у бінарному дереві пошуку виконуються за час, пропорційний його висоті. Для повного бінарного дерева з Бінарне дерево пошуку може бути представлене за допомогою зв'язаної структури даних, в якій кожен вузол є об'єктом Node. На додаток до полів ключа
class Node { public int iData; // data item (key) public double dData; // data item public Node leftChild; // this node’s left child public Node rightChild; // this node’s right child public void displayNode() // display ourself { System.out.print('{'); System.out.print(iData); System.out.print(", "); System.out.print(dData); System.out.print("} "); } } // end class Node
Ключі у бінарному дереві пошуку зберігаються особливим чином, щоб у будь-який момент задовольняти наступній властивості бінарного дерева пошуку: якщо Вставка елементу. Алгоритм вставки елементу починає свою роботу в корені дерева і проходить по низхідному шляху, переміщаючись вліво або управо залежно від результату порівняння ключів, до тих пір, поки не наштовхнеться на незайняту позицію лівого або правого спадкоємця елементу.
public void insert(int id, double dd) { Node newNode = new Node(); // make new node newNode.iData = id; // insert data newNode.dData = dd; if(root==null) // no node in root root = newNode; else // root occupied { Node current = root; // start at root Node parent; while(true) // (exits internally) { parent = current; if(id < current.iData) // go left? { current = current.leftChild; if(current == null) // if end of the line, { // insert on left parent.leftChild = newNode; return; } } // else // or go right? { current = current.rightChild; if(current == null) // if end of the line { // insert on right parent.rightChild = newNode; return; } } // end else go right } // end while } // end else not root } //
Пошук. Для пошуку вузла із заданим ключем у бінарному дереві пошуку використовується наступний алгоритм: для кожного вузла
public Node find(int key) // find node with given key { Node current = root; // start at root while(current.iData != key) { if(key < current.iData) current = current.leftChild; else // or go right? current = current.rightChild; if(current == null) return null; } return current; } // end find()
Видалення елементу. Алгоритм видалення вузла працює по-різному, залежно від того – чи є у елемента, що видаляється, дочірні вузли: - Якщо у вузла, що видаляється, немає дочірніх елементів, то ми просто змінюємо його батьківський вузол, замінюючи в ньому вказівник на елемент, що видаляється, значенням - Якщо у вузла, що видаляється, тільки один дочірній елемент, то ми видаляємо вузол, зв'язуючи батьківський елемент і дочірній елемент вузла, що видаляється. - Якщо у вузла, що видаляється, два дочірні елементи, то знаходимо вузол, що йде за ним, у якого немає лівого дочірнього вузла, прибираємо його з позиції, де він знаходився раніше, шляхом створення нового зв'язку між його батьком і нащадком, і замінюємо ним вузол, що видаляється. Час роботи алгоритму видалення у всіх трьох випадках, для бінарного дерева пошуку заввишки
public boolean delete(int key) // delete node with given key { Node current = root; Node parent = root; boolean isLeftChild = true; while(current.iData != key) // search for node { parent = current; if(key < current.iData) // go left? { isLeftChild = true; current = current.leftChild; } else // or go right? { isLeftChild = false; current = current.rightChild; } if(current == null) // end of the line, return false; // didn’t find it } // end while if(current.leftChild==null && current.rightChild==null) { if(current == root) // if root, root = null; // tree is empty else if(isLeftChild) parent.leftChild = null; // disconnect else // from parent parent.rightChild = null; } else if(current.rightChild==null) if(current == root) root = current.leftChild; else if(isLeftChild) parent.leftChild = current.leftChild; else parent.rightChild = current.leftChild; else if(current.leftChild==null) if(current == root) root = current.rightChild; else if(isLeftChild) parent.leftChild = current.rightChild; else parent.rightChild = current.rightChild; else { Node successor = getSuccessor(current); // connect parent of current to successor instead if(current == root) root = successor; else if(isLeftChild) parent.leftChild = successor; else parent.rightChild = successor; successor.leftChild = current.leftChild; } // end else two children return true; } // end delete Код програми представлений в додатку А.
Контрольні питання 1. Що таке пошук? 2. Що називаються ключем пошуку? 3. Які відомі методи пошуку? 4. Який алгоритм пошуку є найбільш ефективним? 5. Чим відрізняються пошук в масиві від пошуку в списку? 6. У чому полягаю метод лінійного пошуку? 7. Що представляю собоя двійкове дерево? 8. У чому полягає вставка вузла в дерево? 9. У чому полягає видалення вузла з дерева? 10. Які особливості видалення елемента з деревовидної структури даних? 11. У чому полягає пошук в дереві? 12. Що таке «проходження дерева»? Які можливі варіанти проходження дерева? Варіанти завдань
|
|
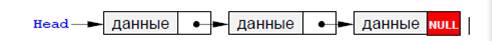
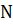порівнянь, де 
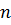вузлами ці операції виконуються за час 
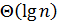у найгіршому випадку. Математичне очікування висоти побудованого випадковим чином бінарного дерева дорівнює 
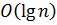, так що усі основні операції над динамічною множиною в такому дереві виконуються в середньому за час 
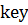і супутніх даних, кожен вузол містить поля leftChild, rightChild, які вказують на лівий, правий дочірні вузли . Якщо дочірній вузол відсутній, відповідне поле містить значення 
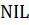. Єдиний вузол, вказівник root– це кореневий вузол дерева.
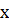– вузол бінарного дерева пошуку, а вузол 
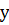знаходиться в лівому піддереві 
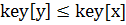. Якщо вузол 
.
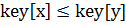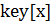порівнюється з шуканим ключем 
. Якщо ключі однакові, пошук завершується. Якщо 
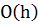, де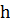 
– висота дерева.
.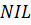