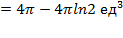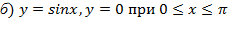|
|
Метод интегрирования по частям
Найдем точки пересечения функций, ограничивающих на плоскости фигуру, которая разбивается на 2 фигуры:
Следует учесть, что фигура ограничена горизонтальной прямой, т.е. при нахождении площади криволинейной трапеции необходимо вычесть площадь квадрата, не включенного в фигуру.
Учебно-методическое и информационное обеспечение дисциплины а) основная литература 1. Геворкян П.С. Высшая математика. Основы математического анализа [Электронный ресурс]: учебник для вузов/ Геворкян П.С.— Электрон. текстовые данные.— М.: ФИЗМАТЛИТ, 2011.— 239 c.— Режим доступа: http://www.iprbookshop.ru/24992.— ЭБС «IPRbooks», по паролю/ 2. Гулиян Б.Ш. Математика. Базовый курс [Электронный ресурс]: учебник/ Гулиян Б.Ш., Хамидуллин Р.Я.— Электрон. текстовые данные.— М.: Московский финансово-промышленный университет «Синергия», 2013.— 712 c.— Режим доступа: http://www.iprbookshop.ru/17023.— ЭБС «IPRbooks», по паролю 3. Ильин В.А. Основы математического анализа. Часть I [Электронный ресурс]: учебник для вузов/ Ильин В.А., Позняк Э.Г.— Электрон. текстовые данные.— М.: ФИЗМАТЛИТ, 2014.— 645 c.— Режим доступа: http://www.iprbookshop.ru/25695.— ЭБС «IPRbooks», по паролю 4. Кремер Н.Ш. Высшая математика для экономистов [Электронный ресурс]: учебник/ Кремер Н.Ш., Путко Б.А., Тришин И.М.— Электрон. текстовые данные.— М.: ЮНИТИ-ДАНА, 2012.— 479 c.— Режим доступа: http://www.iprbookshop.ru/12847.— ЭБС «IPRbooks», по паролю 5. Математика в экономике. Ч. 2. Математический анализ [Электронный ресурс]: учебник/ А.С. Солодовников [и др.].— Электрон. текстовые данные.— М.: Финансы и статистика, 2010.— 560 c.— Режим доступа: http://www.iprbookshop.ru/12435.— ЭБС «IPRbooks».
б) дополнительная литература 6. Бугров, Я.С, Высшая математика: учебник для вузов. В 3-х т. Т.2 / Я.С, Бугров, С.М. Никольский, В.А, Садовничий. – 8-е изд., стереотип. – М.: Дрофа, 2007. 7. Виленкин, И.В. Высшая математика. Интегралы по мере. Дифференциальные уравнения. Ряды: Учебное пособие для студентов экон., техн., естеств.-науч. спец. Вузов / И.В. Виленкин, , Гробер, В.М. – Ростов н/Д: Феникс, 2011. 8. Ганиев В.С. Математический анализ. Часть 1 [Электронный ресурс]: учебное пособие/ Ганиев В.С.— Электрон. текстовые данные.— Самара: Самарский государственный архитектурно-строительный университет, ЭБС АСВ, 2013.— 172 c.— Режим доступа: http://www.iprbookshop.ru/20476.— ЭБС «IPRbooks» 9. Гриб, А.А. Математический анализ для экономистов / А.А. Гриб, А.Ф. Тарасюк. – М.: Филин, 2000. 10. Данко, П.Е. Высшая математика в упражнениях и задачах: В 2-х ч. Т.1,2 / П.Е. Данко, А.Г. Попов, Г.Я. Кожевникова. – М.: Высшая школа, 1999. (в библиотеке ЧИЭП) 11. Демидович, Б.П. Сборник задач и упражнений по математическому анализу: Учебное пособие. – 18-е изд., испр./ Б.П. Демидович, Л.А. Николов. – М.: Изд-во Моск. Ун-та, ЧеРо, 1997. – 624 с. 12. Злобина С.В. Математический анализ в задачах и упражнениях [Электронный ресурс]: учебное пособие/ Злобина С.В., Посицельская Л.Н.— Электрон. текстовые данные.— М.: ФИЗМАТЛИТ, 2009.— 360 c.— Режим доступа: http://www.iprbookshop.ru/12887.— ЭБС «IPRbooks» 13. Ильин, В.А. Основы математического анализа: В 2-х ч.: Учебник для вузов. – 7-е изд., стер. / В.А. Ильин, Э.Г. Позняк. – М.: Физматлит, 2009. – 648 с. 14. Кремер, Н.Ш. Математика для экономистов: от арифметики до эконометрики: Учебно-справ. пособие для бакалавров, студентов вузов, обуч. по спец. 080116 (061800) «Мат. методы в экон.» и др. экон. спец./ Н.Ш. Кремер, Путко, Б.А. – М.: Юрайт, 2012. 15. Математика в экономике. Ч. 2. Математический анализ [Электронный ресурс]: учебник/ А.С. Солодовников [и др.].— Электрон. текстовые данные.— М.: Финансы и статистика, 2010.— 560 c.— Режим доступа: http://www.iprbookshop.ru/12435.— ЭБС «IPRbooks» 16. Солодовников, А.С. Математика в экономике: Учеб.: В 3-х ч. Ч.2 / А.С. Солодовников, В.А. Бабайцев, А.В. Брашов. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2006. 17. Фихтенгольц, Г.М. Курс дифференциального и интегрального исчисления: учебник: В 3-х т. / Г.М. Фихтенгольц. – 8-е изд. – М.: ФИЗМАТЛИТ, 2001. 18. Шипачев, В. С. Высшая математика. Полный курс: Учебник для бакалавров. – М.: Юрайт, 2013 19. Шнейдер В.Е. Курс высшей математики. В 2 книгах. Кн. 1: Учеб. Пособие для вузов / В.Е. Шнейдер, А.И. Слуцкий, А.С. Шумов. 3-е изд., перераб. и испр. – М.: ООО «Мир и образование», 2009. – 544 с.
в том числе Библиотека ЧИЭП 20. Кремер, Н.Ш. Практикум по высшей математике для экономистов. Учебное пособие для ВУЗов. 2-е изд./ Н.Ш. Кремер. – М.: ЮНИТИ – ДАНА, 2005. (в библиотеке ЧИЭП) 21. Кремер, Н.Ш. Высшая математика для экономистов. Учебник для ВУЗов. 2-е изд./ Н.Ш. Кремер. – М.: ЮНИТИ – ДАНА, 2007. (в библиотеке ЧИЭП) 22. Красс, М.С. Математика для экономистов/ М.С. Красс, Б.П. Чупрынов. – СПб.: Питер, 2010. – 464 с. (в библиотеке ЧИЭП) 23. Турецкий, В.Я. Математика и информатика. Учебник. 3-е издание/ В.Я. Турецкий. – М.: ИНФРА–М, 2008. (в библиотеке ЧИЭП)
в) программное обеспечение и Интернет-ресурсы 1. Gaudeamusб ОмскCity [Электронный ресурс]: электронная библиотека он-лайн. – Режим доступа: http:// http://www.gaudeamus.omskcity.com/. – Дата обращения: 11.10.2014. |
|


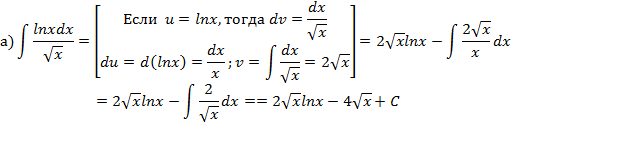
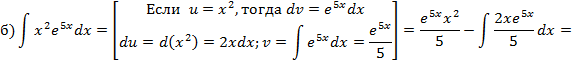
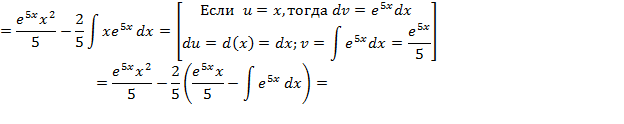
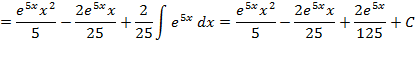





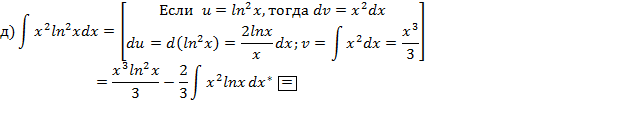
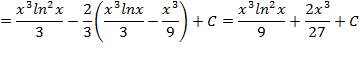
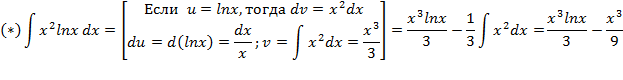
 Найти площадь плоской фигуры
Найти площадь плоской фигуры



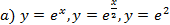
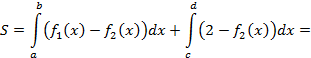

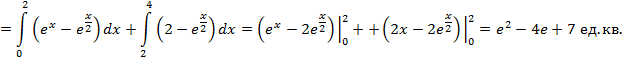
 б)
б) 



 Найти объемы тел, образованных при вращении вокруг осей Ох и Оу плоских фигур, ограниченных линиями:
Найти объемы тел, образованных при вращении вокруг осей Ох и Оу плоских фигур, ограниченных линиями: