|
|
Простейшее уравнение гиперболы
Здесь а - действительная полуось гиперболы, b—мнимая полуось гиперболы. Если 2с — расстояние между фокусами гиперболы, то между а, b и с существует соотношение a2 + b2 = с2 При b= а гипербола называется равносторонней. Уравнение равносторонней гиперболы имеет вид x2 - y2 = a2 фокусы гиперболы лежат на ее действительной оси. Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к длине ее действительной оси е= Асимптоты гиперболы - две прямые, определяемые уравнениями Напомним, что асимптотой кривой, имеющей бесконечную ветвь, называется прямая, которая обладает тем свойством, что когда точка по кривой удаляется в бесконечность, ее расстояние до этой прямой стремится к нулю.
4.Парабола. Параболой называется геометрическое место точек, каждая из которых одинаково удалена от заданной фиксированной точки и от заданной фиксированной прямой. Точка, о которой идет речь в определении, называется фокусом параболы, а прямая — ее директрисой. Простейшее уравнение параболы y2= 2px Входящая в это уравнение величина р называется параметром параболы. Параметр параболы равен расстоянию от директрисы параболы до ее фокуса. Координаты фокуса F параболы F(
Пример. Составить простейшее уравнение гиперболы, если расстояние между вершинами ее равно 20, а расстояние между фокусами 30. Решение: Вершины гиперболы лежат на ее действительной оси. По условию 2а = 20; 2с == 30. Значит, а = 10; с = 15 а2 = 100; с2 = 225. Величины а, и и с у гиперболы связаны соотношением а2 +b2 = с2; отсюда b 2 = с2 —а2 = 225 — 100 Þ b 2 = 125. Значит, уравнением гиперболы будет
Пример. Действительная полуось гиперболы равна 5, эксцентриситет е= 1,4. Найти уравнение гиперболы. Решение: По условию а = 5, значит а2 = 25. По формуле е = Искомым уравнением будет
Пример. Найти уравнение асимптот гиперболы 2x2 - 3y2 = 6. Решение: У гиперболы две асимптоты, определяемые уравнениями Приведем уравнение гиперболы к простейшему виду, разделив обе его части на 6. Получим
Отсюда заключаем, чт а2 = .3, а =
IV. МАТЕМАТИЧЕСКИЙ АНАЛИЗ Функция одной переменной
Если каждому значению переменной х (аргументу) из некоторого множества Х ставится в соответствие одно значение у из множества Y, то говорят, что на множестве Х задана функция f (x)со множеством значений Y, где Х – область определения функции, Y – область значения функции, или у является функцией от х и записывают у = f(x). Если функция задана аналитически, то областью существования функции (иначе, областью значения функции) называется совокупность тех действительных значений аргумента, при которых аналитическое выражение определяющее функцию, принимает только действительные значения. Графиком функции у = f(x) называется множество точек (х, f(x)). Графиком пользуются для геометрического изображения функций. Графики многих функций строят с помощью параллельного переноса, растяжения или сжатия основных элементарных функций: степенной, показательной, логарифмической, тригонометрической и обратных тригонометрических. Функция у = f(x) называется четной, если выполняется равенство Пример: Найти область значения функции:
Решение:
Предел функции.
Число А называется пределом функции при х Функция При вычислении пределов необходимо знать такие теоремы:
Если
Для всех основных элементарных функций в произвольной точке их области определения справедливо равенство
5. Бесконечно малые Если 1. 2. 3. Предел отношений двух бесконечно малых не изменится , если заменить их эквивалентными величинами. При вычислении пределов часто используют: Первый замечательный предел
Второй замечательный предел
Вычисление предела сводится к подстановке в данное выражение предельного значения аргумента. Если при этом получаем неопределенности типа Пример. Найти предел: 1. 2. 3. = 4. = В этом примере неопределенность 5.
в этом примере неопределенность
Непрерывность функции
Функция называется f(x) называется непрерывной в точке х0, , если она определена в некоторой окрестности этой точки и выполняется равенство
где Если хотя бы одно из этих условий не выполняется, то функция называется разрывной в точке х0 . Когда у функции f(x) имеются односторонние пределы Если Если хотя бы один из односторонних пределов Если функция непрерывна в каждой точке некоторого промежутка, то она называется непрерывной на этом промежутке. Алгебраическая сумма, произведение и суперпозиция конечного числа непрерывных функций есть функция непрерывная. Отношение двух непрерывных функций есть функция непрерывная, если знаменатель не равен нулю. Отсюда следует, что всякая элементарная функция непрерывна в точках, в которых она определена. Пример. Исследовать на непрерывность: 1.
.
2. Функция f(x) =
|
|

 .
.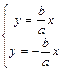
 , 0). Уравнение директрисы параболы
, 0). Уравнение директрисы параболы

 =1,4, отсюда с = 1,4·а = 1,4 · 5 = 7; с2 = 49; b2 = с2 - а2 = 49 — 25 = 24, b2 =24
=1,4, отсюда с = 1,4·а = 1,4 · 5 = 7; с2 = 49; b2 = с2 - а2 = 49 — 25 = 24, b2 =24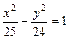

 ; b2 = 2, b ==
; b2 = 2, b ==  . Подставляя эти значения а и b в уравнения асимптот получаем:
. Подставляя эти значения а и b в уравнения асимптот получаем:  ;
; 
 . График четной функции симметричен относительно оси ординат. Функция у = f(x) называется нечетной, если выполняется равенство
. График четной функции симметричен относительно оси ординат. Функция у = f(x) называется нечетной, если выполняется равенство  . График нечетной функции симметричен относительно начала координат.
. График нечетной функции симметричен относительно начала координат.
 .
. , если для любого сколь угодно малого
, если для любого сколь угодно малого  существует число
существует число  такое, что
такое, что  при
при  . Это записывают так:
. Это записывают так:  . Аналогично определяется предел при х
. Аналогично определяется предел при х  .
. называется бесконечно большой при х
называется бесконечно большой при х  и бесконечно малой при х
и бесконечно малой при х  . Аналогично определяются бесконечно большие и бесконечно малые при х
. Аналогично определяются бесконечно большие и бесконечно малые при х  - Const.
- Const. и
и  существуют, то
существуют, то 





 ;
;
 Const.
Const. ,
, 


 и
и  называются эквивалентными при х
называются эквивалентными при х  . Это записывают так:
. Это записывают так: 
 при
при  , то выполняются эквивалентности:
, то выполняются эквивалентности: 4.
4. 
 5.
5. 
 6.
6. 

 или
или 
 , то вычисление этого предела в этом случае называется раскрытием неопределенности.
, то вычисление этого предела в этом случае называется раскрытием неопределенности. , здесь раскрываем неопределенность типа
, здесь раскрываем неопределенность типа  , поделив числитель и знаменатель на
, поделив числитель и знаменатель на  , где n = 5 (наивысшая степень х).
, где n = 5 (наивысшая степень х). , здесь раскрыта неопределенность типа
, здесь раскрыта неопределенность типа  , поделив числитель и знаменатель на (х-2).
, поделив числитель и знаменатель на (х-2).
 ,здесь, раскрывая неопределенность
,здесь, раскрывая неопределенность  .
.
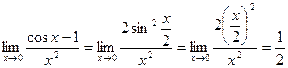 .
.

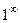 раскрывается с помощью второго замечательного предела.
раскрывается с помощью второго замечательного предела. ,
, ,
,  односторонние (левый и правый) пределы .
односторонние (левый и правый) пределы . и
и  и не все числа f(x0) , f(x0 - 0) и f(x0 + 0) равны между собой , то разрыв в точке х0 называется разрывом I рода. Величина
и не все числа f(x0) , f(x0 - 0) и f(x0 + 0) равны между собой , то разрыв в точке х0 называется разрывом I рода. Величина  называется скачком функции.
называется скачком функции. , то разрыв в точке называется устранимым. Здесь полагая
, то разрыв в точке называется устранимым. Здесь полагая  получают функцию непрерывную в точке х0.
получают функцию непрерывную в точке х0. не существует или равен бесконечности, то разрыв называется разрывом II рода.
не существует или равен бесконечности, то разрыв называется разрывом II рода. имеет в точке х=2 разрыв I рода, поскольку
имеет в точке х=2 разрыв I рода, поскольку  . Скачек функции в точке х=2 равен
. Скачек функции в точке х=2 равен 


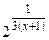 не определена в точке х = -1, потому в этой точке она имеет разрыв. Поскольку
не определена в точке х = -1, потому в этой точке она имеет разрыв. Поскольку  и
и  , то в точке х = -1 функция имеется разрыв II рода.
, то в точке х = -1 функция имеется разрыв II рода.
