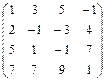Второе достаточное условие существования экстремума
Если в точке х = х0 первая производная функции f (х) = 0, то при х = х0 имеет место максимум, если  < 0, и, минимум, если < 0, и, минимум, если  > 0. Если же > 0. Если же  = 0, то для заключения об экстремуме в этой точке требуется дальнейшее исследование. = 0, то для заключения об экстремуме в этой точке требуется дальнейшее исследование.
Пример. Найти экстремумы функции  . .
Решение. Область определения: 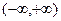
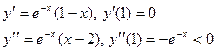
Значит, функция  в точке х = 1 имеет максимум уmax (1) = в точке х = 1 имеет максимум уmax (1) =  1/е. 1/е.
Наибольшее и наименьшее значение функции на отрезке
Если функция f (х) непрерывна на отрезке [а, Ь], то на этом отрезке всегда имеются точки, в которых она принимает наибольшее и наименьшее значения. Этих значений функция достигает или в критических точках, или на концах отрезка [а, Ь]. Поэтому, чтобы определить наибольшее и наименьшее значение функции на отрезке, надо:
определить критическое точка функции;
вычислить значения функции в критических точках и на концах отрезка [а, Ь];
наибольшее из значений, найденных в п. 2, будет наибольшим, а наименьшее - наименьшим значением функции на отрезке [а, Ь].
Точки перегиба.
Говорят, что на интервале (а, Ь) кривая обращена выпуклостью вниз, если она лежит выше касательной, проведенной в любой ее точке.
Говорят, что на интервале (а, Ь) кривая обращена выпуклостью вверх, если она лежит ниже касательной, проведенной в любой ее точке.
Дуги кривой, обращенные выпуклостью вверх, в дальнейшем будем называть выпуклыми, а обращенные выпуклостью вниз,— вогнутыми.
Дуга кривой у = f (х) выпукла на интервале (а, Ь), если во всех точках этого интервала  (х) < 0, и вогнута на этом интервале, если во всех его точках (х) < 0, и вогнута на этом интервале, если во всех его точках  (х) > 0. (х) > 0.
Интервалы, в которых дуги кривой выпуклы, определяются из неравенства  (х) < 0, а интервалы, в которых дуги этой кривой вогнуты, - из неравенства (х) < 0, а интервалы, в которых дуги этой кривой вогнуты, - из неравенства  (х) > 0. (х) > 0.
Точка кривой, отделяющая ее выпуклую дугу от вогнутой, называется точкой перегиба.
Точки, кривой, в которых  (х) = 0 или (х) = 0 или  (х) = (х) = 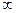 , а также те из них, в которых , а также те из них, в которых  (х) не существует, называются критическими точками второго рода. Точки перегиба следует искать среди критических точек второго рода. (х) не существует, называются критическими точками второго рода. Точки перегиба следует искать среди критических точек второго рода.
В критической точке второго рода х = х0 перегиб будет только в том случае, когда при переходе через эту точку  (х) меняет знак. (х) меняет знак.
Для определения точек перегиба кривой надо определить все критические точки второго рода и рассмотреть знаки  (х) в каждых двух соседних интервалах, на которые эти точки делят область существования функции. В случае, если знаки (х) в каждых двух соседних интервалах, на которые эти точки делят область существования функции. В случае, если знаки  (х) в двух соседних интервалах различны, критическая точка второго рода является точкой перегиба. Если же в двух соседних интервалах (х) в двух соседних интервалах различны, критическая точка второго рода является точкой перегиба. Если же в двух соседних интервалах  (х) имеет один и тот же знак, то в рассматриваемой критической точке второго рода перегиба нет. В точке перегиба кривая пересекает касательную. (х) имеет один и тот же знак, то в рассматриваемой критической точке второго рода перегиба нет. В точке перегиба кривая пересекает касательную.
Пример. Определить интервалы выпуклости и вогнутости и точки перегиба графика функции
у = 5х2 + 20х + 9.
Решение. Область существования функции — интервал  ); );
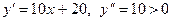
. и так как у" > 0 при любом значении х, то кривая вогнута на всем интервале  ). Точек перегиба нет. ). Точек перегиба нет.
Пример. Определить интервалы выпуклости и вогнутости и точки перегиба графика функции
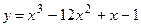
Решение. Область существования функции - интервал  ). ).
Найдем у": 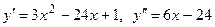 . .
При любом х вторая производная конечна и существует. Критическую точку второго рода найдем из уравнения у" = 0, т.е. из уравнения 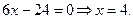 Интервал существования функции она разделяет на два: Интервал существования функции она разделяет на два: 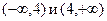 . При любом х из первого интервала у" < 0, а при любом х из второго интервала у" > 0, значит . При любом х из первого интервала у" < 0, а при любом х из второго интервала у" > 0, значит 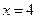 - точка перегиба, а так как на первом интервале у" < 0, то дуга кривой на нем – выпукла, а во втором у" < 0, и дуга кривой вогнута. Координаты точек перегиба (4,-125). - точка перегиба, а так как на первом интервале у" < 0, то дуга кривой на нем – выпукла, а во втором у" < 0, и дуга кривой вогнута. Координаты точек перегиба (4,-125).
Асимптоты.
Если расстояние d от точки кривой у = f (х), имеющей бесконечную ветвь, до некоторой определенной прямой по мере удаления точки по этой кривой в бесконечность стремится к нулю, то прямая называется асимптотой кривой.
Различают асимптоты: 1) горизонтальные, 2) вертикальные и 3) наклонные.
1. Кривая у = f (х) имеет горизонтальную асимптоту у =b только в том случае, когда существует конечный предел функции f (х) при 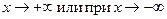 , и этот предел равен b , т. е. если , и этот предел равен b , т. е. если
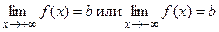
2. Кривая у = f (х) имеет вертикальную асимптоту х = а, если при 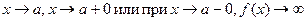 . Для определения вертикальных асимптот надо отыскать те значения аргумента, вблизи которых f (х) неограниченно возрастает по абсолютной величине. Если такими значениями аргумента являются а1, а2, …, то уравнения вертикальных асимптот будут . Для определения вертикальных асимптот надо отыскать те значения аргумента, вблизи которых f (х) неограниченно возрастает по абсолютной величине. Если такими значениями аргумента являются а1, а2, …, то уравнения вертикальных асимптот будут
х = а1, х =а2…
3. Для определения наклонной асимптоты у = kx + b кривой у = f (х) надо найти числа k и b из формул
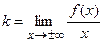
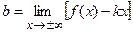
(следует отдельно рассматривать случаи 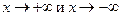 ). Наклонные асимптоты у кривой у = f (х) существуют в том и только в том случае, когда эти пределы имеют конечное значение. При определении этих пределов удобно пользоваться правилом Лопиталя. ). Наклонные асимптоты у кривой у = f (х) существуют в том и только в том случае, когда эти пределы имеют конечное значение. При определении этих пределов удобно пользоваться правилом Лопиталя.
Пример. Найти асимптоты кривой 
Решение. Горизонтальных асимптот нет. Вертикальную асимптоту находим из условия
2х + 3 = 0 => х = - 3/2, при этом у 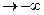 , когда , когда  , у , у 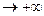 , когда , когда 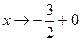 . Определим наклонные асимптоты , уравнение которых имеет вид: у = kx + b . Определим наклонные асимптоты , уравнение которых имеет вид: у = kx + b
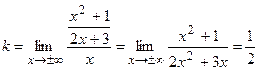

Так как k и b имеют конечные значения и равны между собой при х 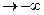 и при х и при х 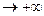 , то имеется единственная наклонная асимптота, уравнение которой , то имеется единственная наклонная асимптота, уравнение которой
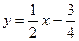
Общее исследование функции
Под полным исследованием функции обычно понимается решение таких вопросов:
- Определение области существования функции.
- Выявление вопроса о четности и нечетности функции.
- Определение точек разрыва функции.
- Определение асимптот графика функции.
- Определение интервалов возрастания и убывания функции.
- Определение экстремума функции.
- Определение интервалов выпуклости и вогнутости графика функции.
- Определение точек перегиба.
- Нахождение пересечения с осями координат.
- Построение графика функции.
Пример. Исследуем функцию 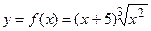
D (y) = ( 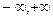 ). Функция непрерывна на всей области определения. Точек разрыва нет. ). Функция непрерывна на всей области определения. Точек разрыва нет.
Функция не является ни четной, ни нечетной, ни периодической.
Точек разрыва нет.
Вертикальных асимптот нет; 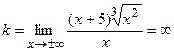 , наклонных асимптот нет. , наклонных асимптот нет.
5, 6.  . Критические точки х = -2, х = 0. . Критические точки х = -2, х = 0.
| х
| ( 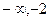 ) )
| -2
| (-2, 0)
|
| ( 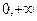 ) )
| Знак 
| +
|  = 0 = 0
| -
| 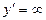
| +
| | Поведение функции
| Возрастает
| max
3 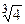
| Убывает
| min
| Возрастает
|
7, 8.  , ,  при х = 1, при х = 1, 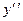 не существует при х = 0. не существует при х = 0.
| х
| ( 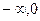 ) )
|
| ( 0, 1)
|
| ( 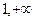 ) )
| Знак 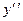
| -
| 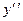 = = 
| -
| 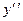 = 0 = 0
| +
| | Поведение функции
| Выпукла верх
| Не является точкой перегиба
| Выпукла верх
| Точка перегиба
у = 6
| Выпукла вниз
|
9. 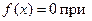 х =0 и х = -5. х =0 и х = -5.
10.

Задание 1
1. Вычислить определитель матрицы А второго порядка
2. Вычислить определитель матрицы В третьего порядка
3. Вычислить определитель матрицы В, разложив его по какой-либо строке и какому либо столбцу
4. Вычислить определитель матрицы В, пользуясь свойствами определителей. Свести вычисление определителя третьего порядка к вычислению одного определителя второго порядка
| Вариант 1
|
|
|
|
|
|
|
|
|
|
| | A =
| (
| -3
| -6
| )
|
| B =
| (
|
| -1
|
| )
| |
|
|
|
|
| -5
| |
|
|
|
|
|
|
| -2
| -4
| | Вариант 2
|
|
|
|
|
|
|
|
|
|
| | A =
| (
|
|
| )
|
| B =
| (
| -1
| -4
| -4
| )
| | -9
| -3
|
| -4
| -1
|
| |
|
|
|
|
|
| -1
|
| -2
| | Вариант 3
|
|
|
|
|
|
|
|
|
|
| | A =
| (
| -1
|
| )
|
| B =
| (
| -5
|
| -3
| )
| | -1
| -8
|
|
| -4
| -4
| |
|
|
|
|
|
| -3
| -1
|
| | Вариант 4
|
|
|
|
|
|
|
|
|
|
| | A =
| (
| -10
| -7
| )
|
| B =
| (
|
| -1
| -2
| )
| |
|
|
| -3
|
|
| |
|
|
|
|
|
| -5
| -5
|
| | Вариант 5
|
|
|
|
|
|
|
|
|
|
| | A =
| (
|
|
| )
|
| B =
| (
| -4
| -4
| -1
| )
| | -5
|
|
|
| -1
| -3
| |
|
|
|
|
|
|
|
| -5
| | Вариант 6
|
|
|
|
|
|
|
|
|
|
| | A =
| (
| -8
| -1
| )
|
| B =
| (
|
|
|
| )
| |
| -3
|
| -2
| -4
|
| |
|
|
|
|
|
|
| -4
| -3
| | Вариант 7
|
|
|
|
|
|
|
|
|
|
| | A =
| (
|
| -8
| )
|
| B =
| (
| -3
| -1
|
| )
| | -9
| -8
|
|
|
| -2
| |
|
|
|
|
|
| -2
|
| -1
| | | | | | | | | | | | | | | | | | |
| Вариант 8
|
|
|
|
|
|
|
|
|
|
| | A =
| (
| -6
|
| )
|
| B =
| (
|
| -4
|
| )
| | -1
|
|
| -1
| -1
|
| |
|
|
|
|
|
| -4
| -3
|
| | Вариант 9
|
|
|
|
|
|
|
|
|
|
| | A =
| (
|
| -2
| )
|
| B =
| (
| -2
|
|
| )
| |
|
|
| -5
| -4
| -1
| |
|
|
|
|
|
|
|
|
| | Вариант 10
|
|
|
|
|
|
|
|
|
|
| | A =
| (
| -4
| -9
| )
|
| B =
| (
|
| -1
| -5
| )
| | -5
| -3
|
|
|
| -5
| |
|
|
|
|
|
|
| -2
| -4
|
Задание 2
1. Решить методом Крамера систему уравнений Ах = а
2. Решить методом Крамера систему уравнений Вx = b
3. Решить методом Гаусса систему уравнений Вx = b
| Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| B =
| (
|
| -3
|
| )
| b=
| (
|
| )
| | A =
| (
|
|
| )
| a=
| (
| -5
| )
|
|
| -1
| -8
| |
| -1
|
|
| -2
| -1
| -3
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| B =
| (
| -4
|
| -3
| )
| b=
| (
|
| )
| | A =
| (
|
|
| )
| a=
| (
|
| )
| -1
| -5
|
|
| | -4
| -2
| -6
| -2
|
|
| -9
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| B =
| (
|
| -4
|
| )
| b=
| (
| -5
| )
| | A =
| (
| -4
| -1
| )
| a=
| (
| -1
| )
|
| -1
| -2
|
| | -1
| -3
| -3
|
| -3
| -2
| -1
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| B =
| (
| -5
|
| -4
| )
| b=
| (
|
| )
| | A =
| (
| -2
| -3
| )
| a=
| (
| -5
| )
| -2
|
|
|
| |
| -4
| -16
| -3
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| B =
| (
| -1
| -5
|
| )
| b=
| (
|
| )
| | A =
| (
|
| -5
| )
| a=
| (
|
| )
|
| -2
| -3
|
| | -4
| -5
|
|
| -4
| -3
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| B =
| (
|
| -1
| -5
| )
| b=
| (
|
| )
| | A =
| (
|
|
| )
| a=
| (
|
| )
| -3
|
|
|
| | -1
|
| -9
| -4
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| B =
| (
| -2
|
| -1
| )
| b=
| (
| -8
| )
| | A =
| (
| -5
|
| )
| a=
| (
| -5
| )
|
| -3
| -4
|
| |
|
|
|
| -5
| -4
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| B =
| (
|
| -2
|
| )
| b=
| (
|
| )
| | A =
| (
| -3
| -2
| )
| a=
| (
| -1
| )
| -4
|
|
|
| | -4
|
|
| -5
| -1
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| B =
| (
| -3
|
| -2
| )
| b=
| (
| -11
| )
| | A =
| (
| -1
| -4
| )
| a=
| (
|
| )
|
| -4
| -5
| -14
| | -1
|
|
| -1
|
| -5
| -10
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| B =
| (
|
| -3
|
| )
| b=
| (
| -5
| )
| | A =
| (
|
|
| )
| a=
| (
| -14
| )
| -5
|
| -1
|
| |
| -1
| -7
|
| -2
| -1
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 3.
1. Решить матричным методом систему уравнений Ах = а
2. Решить матричным методом систему уравнений Вx = b
| Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| B =
| (
|
| -3
|
| )
| b=
| (
|
| )
| | A =
| (
|
| -1
| )
| a=
| (
|
| )
|
|
|
| -2
| -12
| |
| -3
|
|
|
| -2
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| B =
| (
|
|
| -1
| )
| b=
| (
|
| )
| | A =
| (
| -5
| -3
| )
| a=
| (
|
| )
|
| -2
|
| -4
|
| | -2
| -5
|
|
|
|
| -1
| -13
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| B =
| (
| -3
|
| -3
| )
| b=
| (
| -6
| )
| | A =
| (
| -3
| -5
| )
| a=
| (
|
| )
|
|
| -1
|
|
| |
|
| -6
|
| -4
| -5
| -3
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| B =
| (
|
| -3
| -5
| )
| b=
| (
|
| )
| | A =
| (
| -1
|
| )
| a=
| (
| -1
| )
|
| -1
| -2
|
|
| | -5
|
| -5
|
| -2
| -2
| -5
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| B =
| (
|
|
|
| )
| b=
| (
| -5
| )
| | A =
| (
|
|
| )
| a=
| (
| -3
| )
|
| -5
| -3
| -1
|
| | -2
| -2
|
|
|
|
|
| -7
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| B =
| (
| -3
|
|
| )
| b=
| (
| -6
| )
| | A =
| (
|
| -2
| )
| a=
| (
|
| )
|
|
| -4
| -3
|
| |
| -4
| -6
|
|
| -5
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| B =
| (
|
| -3
| -2
| )
| b=
| (
|
| )
| | A =
| (
| -4
| -4
| )
| a=
| (
| -4
| )
|
| -4
| -5
| -5
|
| | -5
|
|
|
| -5
| -2
| -2
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| B =
| (
|
|
| -4
| )
| b=
| (
|
| )
| | A =
| (
| -2
|
| )
| a=
| (
| -21
| )
|
|
|
|
| -3
| | -2
|
| -11
|
| -3
|
| -4
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| B =
| (
| -3
|
|
| )
| b=
| (
| -15
| )
| | A =
| (
|
|
| )
| a=
| (
| -4
| )
|
| -3
|
|
| -16
| |
| -1
|
|
| -1
| -5
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| B =
| (
|
| -3
|
| )
| b=
| (
| -2
| )
| | A =
| (
|
| -1
| )
| a=
| (
| -7
| )
|
|
|
| -2
|
| | -5
| -3
|
|
|
| -2
|
| -2
|
Задание 4.
Вычислить ранг матрицы.
1.  , 2. , 2. 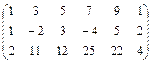 ; ;
3.  4. 4. 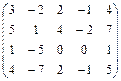
5. 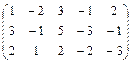 6. 6. 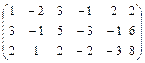
7. 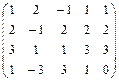 8 8 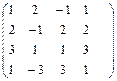
9. 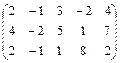 10. 10. 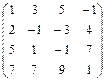
Задание 5
Даны две вершины треугольника Δ АВС: А (х1,у1), В (х2,у2) и точка D (x3,y3)пересечения высот:
а) составить уравнение высот, медиан, биссектрис треугольника Δ АВС.
б) найти уравнения прямых, проходящих через вершины треугольника и параллельных сторонам.
в) определить длины высот треугольника и расстояние от точки М (х4, у4) до сторон треугольника.
|
 < 0, и, минимум, если
< 0, и, минимум, если  .
.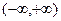
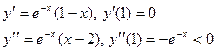
 1/е.
1/е.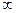 , а также те из них, в которых
, а также те из них, в которых  );
);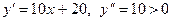
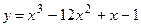
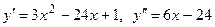 .
.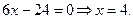 Интервал существования функции она разделяет на два:
Интервал существования функции она разделяет на два: 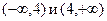 . При любом х из первого интервала у" < 0, а при любом х из второго интервала у" > 0, значит
. При любом х из первого интервала у" < 0, а при любом х из второго интервала у" > 0, значит 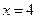 - точка перегиба, а так как на первом интервале у" < 0, то дуга кривой на нем – выпукла, а во втором у" < 0, и дуга кривой вогнута. Координаты точек перегиба (4,-125).
- точка перегиба, а так как на первом интервале у" < 0, то дуга кривой на нем – выпукла, а во втором у" < 0, и дуга кривой вогнута. Координаты точек перегиба (4,-125).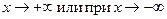 , и этот предел равен b , т. е. если
, и этот предел равен b , т. е. если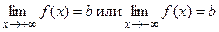
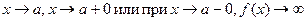 . Для определения вертикальных асимптот надо отыскать те значения аргумента, вблизи которых f (х) неограниченно возрастает по абсолютной величине. Если такими значениями аргумента являются а1, а2, …, то уравнения вертикальных асимптот будут
. Для определения вертикальных асимптот надо отыскать те значения аргумента, вблизи которых f (х) неограниченно возрастает по абсолютной величине. Если такими значениями аргумента являются а1, а2, …, то уравнения вертикальных асимптот будут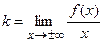
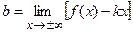
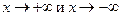 ). Наклонные асимптоты у кривой у = f (х) существуют в том и только в том случае, когда эти пределы имеют конечное значение. При определении этих пределов удобно пользоваться правилом Лопиталя.
). Наклонные асимптоты у кривой у = f (х) существуют в том и только в том случае, когда эти пределы имеют конечное значение. При определении этих пределов удобно пользоваться правилом Лопиталя.
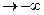 , когда
, когда  , у
, у 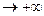 , когда
, когда 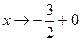 . Определим наклонные асимптоты , уравнение которых имеет вид: у = kx + b
. Определим наклонные асимптоты , уравнение которых имеет вид: у = kx + b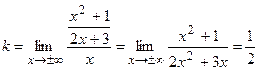

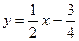
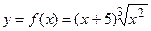
 ). Функция непрерывна на всей области определения. Точек разрыва нет.
). Функция непрерывна на всей области определения. Точек разрыва нет.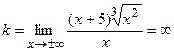 , наклонных асимптот нет.
, наклонных асимптот нет. . Критические точки х = -2, х = 0.
. Критические точки х = -2, х = 0.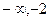 )
)
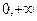 )
)

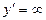
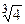
 ,
,  при х = 1,
при х = 1, 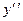 не существует при х = 0.
не существует при х = 0. )
)
 )
)

 х =0 и х = -5.
х =0 и х = -5.
 , 2.
, 2. 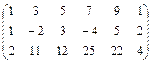 ;
; 4.
4. 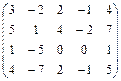
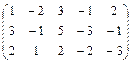 6.
6. 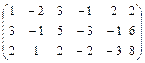
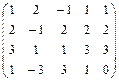 8
8 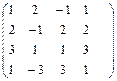
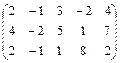 10.
10.