|
|
с помощью математического маятника
Математический маятник – это материальная точка на длинной, невесомой и нерастяжимой нити. На практике математическим маятником считают небольшой шарик, подвешенный к длинной тонкой нити (рис. 23). При этом При малых амплитудах (a £ 60) такая система совершает гармонические колебания с частотой w0. Возвращающая сила F, как следует из рис. 23, равна
Знак «минус» показывает, что вектор силы Из DОАВ (рис. 23) видно, что
где коэффициент пропорциональности
С другой стороны, из теории гармонических колебаний следует, что коэффициент К равен
Приравнивая правые части выражений (2-15) и (2-16), получим соотношение:
Учитывая, что циклическая частота w0 связана с периодом Т колебаний:
можно записать выражение периода колебаний математического маятника, подставив последнее выражение в формулу (2-17).
Запишем формулу (2-18) для двух маятников с длинами
Вычитая из одного уравнения другое, получим
Выразим отсюда ускорение свободного падения.
(где t – время n полных колебаний), можно рассчитать ускорение свободного падения g по формуле (2-19). Экспериментальная установка показа- Рис.24 на на рис. 24. Смещая кольцо вдоль стойки, можно менять длину нити. Методика измерения длины
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Смещая кольцо (рис. 24) по стойке вверх, установите максимально возможную длину 2. Отведите шарик от положения равновесия на небольшой угол (a £ 60, т.е. примерно Х = 10 см при длине нити Отпустив шарик, одновременно включите секундомер и измерьте время n = 10 полных колебаний. Запишите t1 в табл. 14. 3. Повторите опыт (п.2) не менее 7 раз для заданной длины 4. Повторите опыты (п.п.2,3) с другой длиной маятника 5. По формуле (2-19) рассчитайте ускорение свободного падения gi для каждого опыта и найдите среднее значение <g>. Результаты занесите в табл. 14.
Таблица 14
6. Оцените случайную погрешность Dg по формуле Стьюдента; найдите относительную погрешность и запишите ответ в виде: 7. Сравните <g> с табличным значением gт = 9,81 м/с2, округлив его с той же точностью, что и <g>. Сделайте вывод.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Как записывается закон всемирного тяготения? Как направлена сила тяготения? Что характеризует гравитационная постоянная? 2. Что называется силой тяжести? Как она направлена? Можно ли утверждать, что Р = Fт? 3. Чем обусловлена центробежная сила, действующая на тело на поверхности Земли? От чего она зависит? Как меняется центробежная сила при переносе точки с полюса на экватор? 4. От каких факторов зависит сила тяжести? Как обосновать эти зависимости? Как меняется сила тяжести на полюсе по сравнению с экватором? 5. Что называется свободным падением? С каким ускорением тело свободно падает? Как показать, что ускорение g одинаково для всех тел, независимо от их массы? 6. С одинаковой высоты h бросили с одинаковой начальной скоростью u0 три тела: первое – вверх; второе – вниз и третье – в горизонтальном направлении. С каким ускорением движется каждое тело? Какое из этих тел быстрее упадет на Землю? 7. Выберите ответы, относящиеся к определению свободного падения. Свободное падение – это движение … 1) равномерное с u = const; вертикально вниз; 2) равноускоренное с ускорением g = const, согласно уравнения: 3) под действием только силы тяжести; 4) обусловленное вращением земли вокруг оси; 5) равнозамедленное вертикально вниз с ускорение g; 6) сложное, представляющее собой наложение равноускоренного движения вдоль оси Y с ускорением g и равномерного вдоль оси Х с начальной скоростью u0. 8. Какие методы определения ускорения свободного падения существуют? Опишите подробно один из методов определения g (с выводом рабочей формулы). 9. Тело брошено с поверхности земли вверх с начальной скоростью u0. Начертить графики пути h(t), скорости u(t) и ускорения а(t). Сопротивление воздуха не учитывать. 10. За последнюю секунду своего падения шарик прошел путь в 9 раз больше, чем за первую секунду. С какой высоты и сколько времени тело падало? 11. На какой высоте скорость тела, брошенного вертикально вверх, уменьшится в 2 раза? а) в) 12. Тело свободно падает с высоты 80 м. Каково его перемещение в последнюю секунду падения? а) 35 м; б) 80м; в) 5 м; г) 45 м 13. Стрела, выпущенная из лука вертикально вверх, упала на Землю через 6 с. Какова начальная скорость стрелы и максимальная высота подъема? а) u0 = 60 м/с; б) u0 = 30 м/с; в) u0 = 0; г) u0 = 20 м/с h = 180 м h = 45 м h = 90 м h = 60 м 14. Из точки, расположенной на достаточно большой высоте, одновременно брошены два тела с одинаковой начальной скоростью u0 = 2 м/с: одно – вертикально вверх, а другое вертикально вниз. Как будет меняться расстояние между телами с течением времени?
ЛАБОРАТОРНАЯ РАБОТА №3
ИЗУЧЕНИЕ ЗАКОНОВ ДИНАМИКИ НА МАШИНЕ АТВУДА
Цель работы: проверка второго закона Ньютона.
Оборудование: машина Атвуда; набор грузов; секундомер.
Основным законом динамики материальной точки является второй закон Ньютона, смысл которого заключается в том, что геометрическая сумма всех сил, действующих на точку, сообщает ей ускорение, пропорциональное результирующей силе и обратно пропорциональна массе.
где Если на два тела различной массы
С другой стороны, если на два тела одинаковой массы
Целью данной лабораторной работы является проверка соотношений (3-2) и (3-3). Для этой цели служит установка, называемая машиной Атвуда, которая схематически изображена на рис. 26. Общий вид показан на рис. 27. На верхнем конце стойки 1 укреплен блок 2. Через блок перекинута нить 3, к которой привязаны два груза одинаковой массы
Уравнения движения в скалярной форме имеют вид: а) для левого груза: б) для правого груза: Решая совместно эти два уравнения, получим теоретическое выражение для ускорения системы тел.
При равноускоренном движении правого груза с высоты h1 (рис.27, общий вид установки) ускорение будет равно
Отсюда время
Перегрузок
Отсюда выразим скорость u0 и подставим в формулу (3-6). Получим соотношение
Все величины (h1, h2, t2), входящие в последнюю формулу, можно легко измерить. Поэтому выражение (3-7) дает экспериментальное значение ускорения. Поместив на правый груз перегрузок другой массы
где h – высота, с которой правый груз опускается за время t1. Переложив меньший перегрузок на левый груз (масса системы при этом не изменяется), изменяем действующую силу. Ускорение в этом случае будет равно
Раздели (3-8) на (3-9). Получим
Отношение действующих сил в рассмотренном случае будет равно
Согласно выражения (3-3), правые части (3-10) и (3-11) должны быть одинаковыми, т.е.
Проверка соотношения (3-12) является целью данной лабораторной работы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Установите кольцо 5 (рис. 27) на некоторой высоте h1 от начала шкалы. Запишите в табл. 14 значение h1 расстояние от кольца до «ловушки» h2. 2. Положите на правый груз перегрузок 3. Повторите опыт (п.2) не менее 3 раз при тех же значениях h1. Результаты занесите в табл. 14. Найдите среднее значение <t2>. 4. По формуле (3-7) рассчитайте экспериментальное значение ускорения аэ по среднему значению времени <t2>. 5. Повторите опыты (п.п.2-4) с другим перегрузком 6. Оцените относительную погрешность эксперимента по формуле:
где Dh и Dt – половина цены деления шкалы линейки и секундомера соответственно. Абсолютную погрешность найдите по формуле: 7. По формуле (3-4) рассчитайте теоретическое значение ускорения ат. Сравните ат и аэ. Сделайте вывод. 8. Положите оба перегрузка 9. Переложив меньший перегрузок на левый груз (больший перегрузок остается на правом грузе), повторите опыты по измерению времени t2 на участке h1. Результаты занесите в табл. 15 (полож. 2). 10. Рассчитайте средние значения <t1> и <t2>. Найдите значения <t1>2 и <t2>2 и отношение (а1/а2) по формуле (3-10), а также отношение действующих сил (F1/F2) по формуле (3-11). Результаты занесите в табл. 15. Проверьте справедливость уравнения (3-12) и сделайте вывод.
Таблица 14
Таблица 15
КОНТРОЛЬНЫЕ ВОПРОСЫ
2. Что называется ускорением? В каких единицах оно измеряется? Рис. 28 3. Что означает термин «сила»? В каких единицах она измеряется? 4. Что характеризует масса тела? Как можно измерить массу?
6. Какие соотношения проверяются в данной работе? Как обеспечивается постоянство массы системы при проверке соотношения между действующими силами и ускорениями?
8. Тело массой m движется прямолинейно с ускорением a по горизонтальной поверхности под действием силы F, направленной под углом к a к горизонту. Определить величину этой силы, если а) поверхность идеально гладкая; б) коэффициент трения равен К (рис. 29). 9. Нарушится ли равновесие весов (рис. 30), если шарик погрузить в воду, опустив штангу штатива так, чтобы шарик не касался ни дна, ни стенок сосуда? Груз какой массы и на какую чашу весов надо положить, чтобы восстановить равновесие?
ЛАБОРАТОРНАЯ РАБОТА №4
ИЗУЧЕНИЕ НЕПРУГОГО УДАРА И ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО МАЯТНИКА
1) знакомство с методом баллистического маятника; 2) проверка законов сохранения импульса и энергии при неупругом ударе.
Оборудование: баллистический маятник; пневматическое ружье; набор пуль Баллистический маятник (рис. 31) представляет собой коробку, заполненную пластилином или песком. Коробка подвешивается на четырех длинных нитях (бифилярный подвес). Маятник снабжен указателем для удобства отсчета горизонтального смещения после попадания в него пули. Выстрел производится в переднюю (открытую) стенку неподвижного маятника. При попадании пули массой m в неподвижный маятник массой М он отклоняется от вертикали, приобретая в момент удара скорость
где Таким образом, после удара пули о маятник он приходит в движение со скоростью
Решая совместно уравнения (4-1) и (4-2), получим выражение скорости пули перед ударом:
Учитывая, что масса пули во много раз меньше массы маятника (m << М), последнее выражение упростим
Высоту h, на которую поднимается центр масс маятника при отклонении от вертикального положения, найдем из подобия треугольников АКВ и АОД (рис. 31). Введем обозначения: ОД =
Отсюда высота h будет равна
Подставим это значение h в формулу (4-3), окончательно получим
Таким образом, скорость пули u можно определить по отклонению S маятника при попадании в него пули (удар неупругий). Все остальные величины (М, m, Сравнивая кинетическую энергию пули до удара и кинетическую энергию системы «маятник-пуля» после удара, можно убедиться, что при неупругом ударе кинетическая энергия системы уменьшается, т.е.
где кинетическая энергия пули до удара
кинетическая энергия системы «маятник-пуля» после попадания в маятник пули равна
где
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Ознакомьтесь с инструкцией обращения с пневматическим ружьем и правилами ТБ. После получения допуска со стороны преподавателя можно приступать к выполнению эксперимента.
2. Убедитесь в том, что коробка маятника занимает строго горизонтальное положение (длина всех четырех нитей должна быть строго одинаковой). Отметьте по шкале номер деления (n0), против которого находится указатель маятника (рис. 31) и запишите его значение в табл. 16. 3. Произведите выстрелы пулями, отмечая каждый раз номер деления ni, до которого отклоняется указатель маятника после каждого выстрела. Запишите значения ni в табл. 16.
4. Для каждого опыта рассчитайте горизонтальное смещение указателя: Si = ni – n0. Запишите все значения Si в табл. 16, выразив их в метрах. 5. По формуле (4-4) рассчитайте скорость пули ui для каждого опыта. Найдите среднее значение <u>. Значения m, M, Таблица 16
При расчетах не забывайте учитывать увеличение массы маятника после каждого выстрела на величину m. 6. Оцените случайную погрешность Du по формуле Стьюдента. Найдите относительную погрешность. Результат запишите в виде: 7. Рассчитайте среднюю массу маятника (см. выше). Значение <M> запишите в табл. 17. 8. Выразив из формулы (4-1) скорость маятника с пулей (<U>), рассчитайте ее по среднему значению <u> и <M>. Результат запишите в табл.17.
Таблица 17
9. Рассчитайте кинетическую энергию системы до и после попадания пули в маятник соответственно по формулам (4-5) и (4-6). Результаты занесите в табл. 17. 10. Рассчитайте долю энергии пули, превратившуюся во внутреннюю в результате неупругого удара:
рассчитав предварительно изменение энергии
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется импульсом движения? Как формулируется закон сохранения импульса для изолированной системы? 2. Какой удар с энергетической точки зрения называется неупругим? 3. Как записывается закон сохранения импульса и энергии при «неупругом» попадании пули в маятник? 4. Как рассчитать потерю кинетической энергии при неупругом ударе (пуля застряла в маятнике)?
6. На нити подвешен шар массой М (рис.32). Пуля, летящая горизонтально со скоростью u0, попадает в него. Сравнить углы a отклонения шара от вертикали, если: а) пуля застряла в нем; б) пуля пробив шар, летит дальше со скоростью u = u0/2; в) пуля упруго отскакивает от шара; г) пуля, ударившись о шар, падает вниз. Записать закон сохранения импульса и энергии для каждого случая. Масса пули m << M. 7. Центры шаров 1,2,3 расположены на одной прямой (рис. 33). Массы шаров 3m, 2m, m. Шар 1 со скоростью u0 ударяет по неподвижному шару 2, который получив после удара некоторую скорость, ударяет шар 3. Оба удара абсолютно неупругие. Какую скорость приобретут шары в результате удара? Какая часть кинетической энергии первого шара перейдет во внутреннюю в результате соударения со вторым шаром и какая часть кинетической энергии второго шара перейдет во внутреннюю при ударе с шаром 3?
ЛАБОРАТОРНАЯ РАБОТА №5
ИЗУЧЕНИЕ ЦЕНТРАЛЬНОГО УПРУГОГО УДАРА ШАРОВ
Цель работы: 1) изучение упругого удара на примере соударения шаров, подвешенных на нитях; 2) проверка законов сохранения импульса и энергии при упругом ударе шаров
Оборудование: установка для изучения удара шаров; набор шаров раличной массы.
Под ударом в физике понимают явление изменения скоростей взаимодействующих тел на конечную величину за очень короткий промежуток времени.
Относительная скорость реальных тел после удара отличается от скорости тел до удара. Это объясняется тем, что в реальных условиях нет абсолютно упругих тел и идеально гладких поверхностей. Величина, равная отношению относительной скорости тел после удара к их относительной скорости до удара, называется коэффициентом восстановления.
где Если коэффициент восстановления g = 1, удар называется абсолютно упругим; если g = 0 – абсолютно неупругим. Коэффициент восстановления реальных тел лежит в интервале от 0 до 1, т.е. 0 £ g £ 1. Например, для стальных шаров g = 0,6 ¸ 0,7; для шаров из слоновой кости g = 0,9; для свинца g » 0. В момент удара возникают кратковременные ударные силы взаимодействия между телами, которые во много раз превосходят внешние силы, действующие на тела. Поэтому систему соударяющихся тел можно считать изолированной, для которой выполняются законы сохранения импульса и энергии.
Если одно тело до удара покоилось (например, u2 = 0), то уравнения примут вид:
Решая систему уравнений (5-2) и (5-3), получим выражение для определения скоростей после удара.
 (5-4) (5-4)
Пусть шар 1 отклонили от вертикали на угол a (рис. 35) и отпустили. Скорость первого шара в момент удара найдем из закона сохранения механической энергии:
Отсюда
Из рис. 35 следует, что высота h1, на которую поднимется центр масс первого шара, будет равна
Рассуждая аналогично, найдем скорости шаров после удара (рис.37).
где b1 и b2 – углы отклонения шаров от вертикали после удара. Таким образом, измерив углы a (до удара), b1 и b2 (после удара), можно рассчитать скорости шаров до удара (u1) и после удара (U1, U2) и коэффициент восстановления g.
При нажатии «Сброс» на электронном секундомере 8 включается электромагнит; а при нажатии клавиши «Пуск» он отключается. В момент соударения шаров секундомер автоматически отключается, что позволяет измерить продолжительность удара.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Подвесьте два шара различной массы (по указанию преподавателя). Добейтесь их точной центровки, укорачивая или удлиняя соответствующую нить с помощью валиков подвески (рис. 37). Установите электромагнит в крайнее положение в конце шкалы 5. Измерьте линейкой длину нитей подвеса от точки крепления до центра шарика и значение Таблица 18
2. Включите установку в сеть (220 В) и нажмите клавишу «Сеть». На цифровом индикаторе при этом должны высветиться нули. Отклоните от вертикали правый шар, подводя его к электромагниту. Нажмите кнопку «Сброс» на секундомере. В табл. 19 запишите значения угла a1 (в градусах), на который отклонили шар от вертикали. 3. Нажмите кнопку «Пуск», отключив тем самым электромагнит и одновременно включив секундомер. После первого соударения шаров зафиксируйте (визуально) углы b1 и b2 отклонения шаров 1 и 2 соответственно (рис. 36) и занесите их значения в табл. 19. Таблица 19
4. Опыт (п.п.2-3) повторите не менее 3 раз, отклоняя правый шар 1 на один и тот же угол a1. Результаты занесите в табл. 19. Найдите средние значения углов <b1> и <b2>. 5. Для каждого опыта рассчитайте скорости шаров до и после удара по формулам (5-7), (5-8) и (5-9) и коэффициент восстановления g - по формуле (5-1). Результаты занесите в табл. 19. Найдите средние значения <u1>, <U1>, <U2> и <g>. 6. Оцените случайные погрешности Du1, DU1 и DU2 по формуле Стьюдента. Найдите относительные погрешности eu1, eU1 и eU2. Результаты запишите в виде: Х= <Х> ± DХ. 7. Повторите опыты (п.п. 2-6) при другом значении a, изменяя a на несколько градусов (по указанию преподавателя). Результаты занесите в табл. 19, продолжив ее вниз. 8. Сравните скорости шаров U1 и U2 при разных углах a. Сделайте вывод. 9. Рассчитайте импульсы шаров до (Р1) и после удара Таблица 20
10. Сравните сумму импульсов шаров после удара 11. Рассчитайте кинетические энергии шаров: первого шара W1 и
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что в физике понимают под ударом? Какой удар называется прямым центральным? 2. Что называется коэффициентом восстановления? В каких пределах он может изменяться? Какой удар называется абсолютно упругим и абсолютно неупругим? 12 |
|
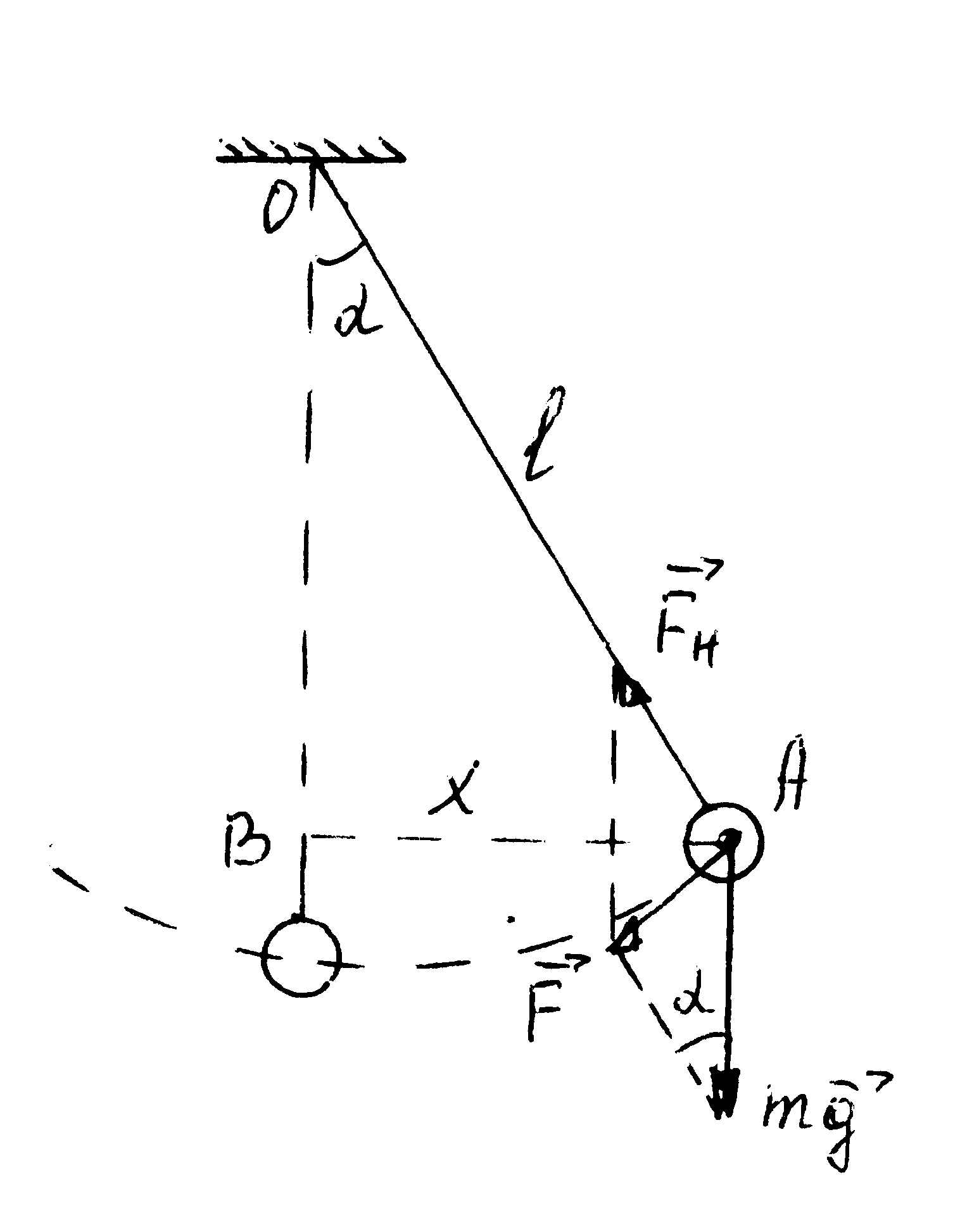 Рис. 23
Рис. 23
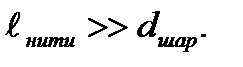
 (2-13)
(2-13) всегда направлен против смещения
всегда направлен против смещения  точки, т.е. вектор
точки, т.е. вектор  всегда направлен в сторону положения равновесия.
всегда направлен в сторону положения равновесия. Подставив значение sin a в формулу (2-13), получим
Подставив значение sin a в формулу (2-13), получим (2-14)
(2-14) (2-15)
(2-15)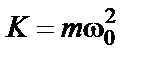 (2-16)
(2-16) (2-17)
(2-17)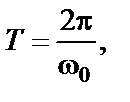
 (2-18)
(2-18) и
и 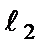
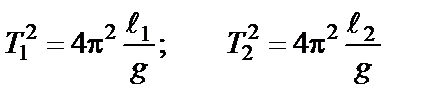
 .
. . (2-19)
. (2-19) Таким образом, измерив длины
Таким образом, измерив длины  и
и  и, определив период колебаний в каждом случае по формуле:
и, определив период колебаний в каждом случае по формуле: (2-20)
(2-20) понятна из рис. 24. При
понятна из рис. 24. При  < 1 м ее измеряют от центра шарика до точки подвеса по вертикали.
< 1 м ее измеряют от центра шарика до точки подвеса по вертикали. Измерив
Измерив  с помощью линейки, запишите ее значение в табл. 14.
с помощью линейки, запишите ее значение в табл. 14. = 1 м) в направлении, перпендикулярном плоскости, образованной нитями.
= 1 м) в направлении, перпендикулярном плоскости, образованной нитями. нити, отклоняя маятник каждый раз на один и тот же угол a.
нити, отклоняя маятник каждый раз на один и тот же угол a. , сместив кольцо К (рис. 24) вниз не менее, чем на 1/3 от
, сместив кольцо К (рис. 24) вниз не менее, чем на 1/3 от  . Результат занесите в табл. 14.
. Результат занесите в табл. 14.


 ;
; ; б)
; б)  ;
; ; г)
; г) 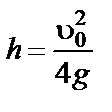
 (3-1)
(3-1) - результирующая всех сил, действующих на материальную точку; m – масса точки.
- результирующая всех сил, действующих на материальную точку; m – масса точки. подействовать одинаковой силой F, то они получат различные ускорения а1 и а2, которые будут удовлетворять условию:
подействовать одинаковой силой F, то они получат различные ускорения а1 и а2, которые будут удовлетворять условию: (3-2)
(3-2) подействовать различными силами
подействовать различными силами  то
то (3-3)
(3-3) Если на один из грузов положить перегрузок
Если на один из грузов положить перегрузок  то система придет в движение.
то система придет в движение. Рассмотрим силы, действующие на систему тел (рис. 26) и запишем уравнения движения грузов. В условиях данной лабораторной работы массой блока 2 и трением в подшипниках пренебрегаем. Поэтому приближенно можно считать, что силы натяжения нитей одинаковы:
Рассмотрим силы, действующие на систему тел (рис. 26) и запишем уравнения движения грузов. В условиях данной лабораторной работы массой блока 2 и трением в подшипниках пренебрегаем. Поэтому приближенно можно считать, что силы натяжения нитей одинаковы: 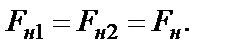
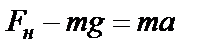
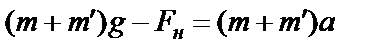
 . (3-4)
. (3-4) . (3-5)
. (3-5) Рис. 27
Рис. 27
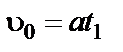
 Подставим это значение t1 в формулу (3-5). Получим
Подставим это значение t1 в формулу (3-5). Получим (3-6)
(3-6) при прохождении сквозь кольцо 5 остается на нем, а груз m движется дальше с постоянной скоростью u0 на участке h2 до момента падения на «ловушку» 6 (рис. 27). Время, затраченное на прохождение пути h2, равно
при прохождении сквозь кольцо 5 остается на нем, а груз m движется дальше с постоянной скоростью u0 на участке h2 до момента падения на «ловушку» 6 (рис. 27). Время, затраченное на прохождение пути h2, равно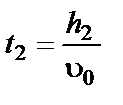
 (3-7)
(3-7) изменим тем, самым действующую силу. Для проверки соотношения (3-3) поступают следующим образом. Оба перегрузка
изменим тем, самым действующую силу. Для проверки соотношения (3-3) поступают следующим образом. Оба перегрузка  и
и  помещают на правый груз. Ускорение, которое приобретает система в этом случае, будет равно
помещают на правый груз. Ускорение, которое приобретает система в этом случае, будет равно (3-8)
(3-8) . (3-9)
. (3-9) . (3-10)
. (3-10) (3-11)
(3-11) (3-12)
(3-12) (диаметр его должен быть больше диаметра кольца). Оба груза (левый и правый) должны находиться на одном уровне. Опустив грузы, включите секундомер в момент прохождения правого груза сквозь кольцо (перегрузок остается на кольце) и выключите его в момент падения груза в «ловушку». Запишите в табл. 14 значение времени t2 прохождения грузом расстояния h2.
(диаметр его должен быть больше диаметра кольца). Оба груза (левый и правый) должны находиться на одном уровне. Опустив грузы, включите секундомер в момент прохождения правого груза сквозь кольцо (перегрузок остается на кольце) и выключите его в момент падения груза в «ловушку». Запишите в табл. 14 значение времени t2 прохождения грузом расстояния h2. , но при тех же значениях h1 и h2. Результаты занесите в табл. 14. Сравните значения аэ(1) и аэ(2). Сделайте вывод.
, но при тех же значениях h1 и h2. Результаты занесите в табл. 14. Сравните значения аэ(1) и аэ(2). Сделайте вывод.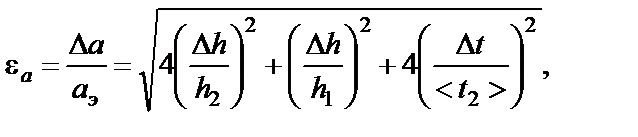
 Результат запишите в виде:
Результат запишите в виде: 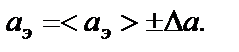
 на правый груз (положение 1). Измерьте время падения t1 на участке h1 не менее 3 раз. Результаты занесите в табл. 15 (полож. 1).
на правый груз (положение 1). Измерьте время падения t1 на участке h1 не менее 3 раз. Результаты занесите в табл. 15 (полож. 1). = ….. г
= ….. г
 = ….. г
= ….. г


 1. Как формулируются законы Ньютона? Каков их физический смысл? Для каких систем отсчета они справедливы?
1. Как формулируются законы Ньютона? Каков их физический смысл? Для каких систем отсчета они справедливы? Рис. 29
Рис. 29
 Рис. 30
Рис. 30
 Рис. 31
Рис. 31
 . По закону сохранения импульса суммарный импульс изолированной системы не изменяется, т.е.
. По закону сохранения импульса суммарный импульс изолированной системы не изменяется, т.е. (4-1)
(4-1) – скорость пули до удара;
– скорость пули до удара;  – скорость, приобретаемая маятником после попадания в него пули.
– скорость, приобретаемая маятником после попадания в него пули. . После удара система «маятник-пуля» обладает кинетической энергией, которая будет переходить в потенциальную (при отклонении маятника от положения равновесия его центр масс поднимается на высоту h – рис. 32). По закону сохранения энергии для изолированной системы тел имеем
. После удара система «маятник-пуля» обладает кинетической энергией, которая будет переходить в потенциальную (при отклонении маятника от положения равновесия его центр масс поднимается на высоту h – рис. 32). По закону сохранения энергии для изолированной системы тел имеем (4-2)
(4-2)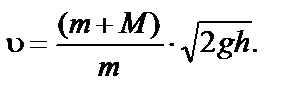
 (4-3)
(4-3) - длина нитей маятника; КВ = h – высота подъема центра масс маятника; АК = S – горизонтальное смещение указателя маятника. В силу того, что h << S, можно приближенно считать ДВ » s/2. Тогда
- длина нитей маятника; КВ = h – высота подъема центра масс маятника; АК = S – горизонтальное смещение указателя маятника. В силу того, что h << S, можно приближенно считать ДВ » s/2. Тогда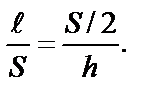
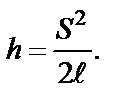
 (4-4)
(4-4) ) заданы на установке.
) заданы на установке.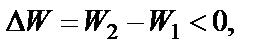
 (4-5)
(4-5) (4-6)
(4-6) - средняя масса маятника после N выстрелов (после каждого выстрела масса маятника увеличивается на массу пули m).
- средняя масса маятника после N выстрелов (после каждого выстрела масса маятника увеличивается на массу пули m). указаны на установке. Результаты занесите в табл. 16.
указаны на установке. Результаты занесите в табл. 16. , м
, м
 .
. (4-7)
(4-7) (4-8)
(4-8) Результаты занесите в табл. 17. Сделайте выводы.
Результаты занесите в табл. 17. Сделайте выводы. Рис. 32
Рис. 32
 Рис. 34
Рис. 34
 (5-1)
(5-1) - скорости тел до удара;
- скорости тел до удара;  - скорости тел после удара.
- скорости тел после удара.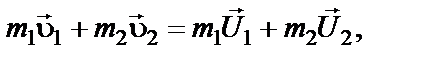
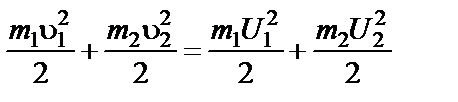
 (5-2)
(5-2) (5-3)
(5-3)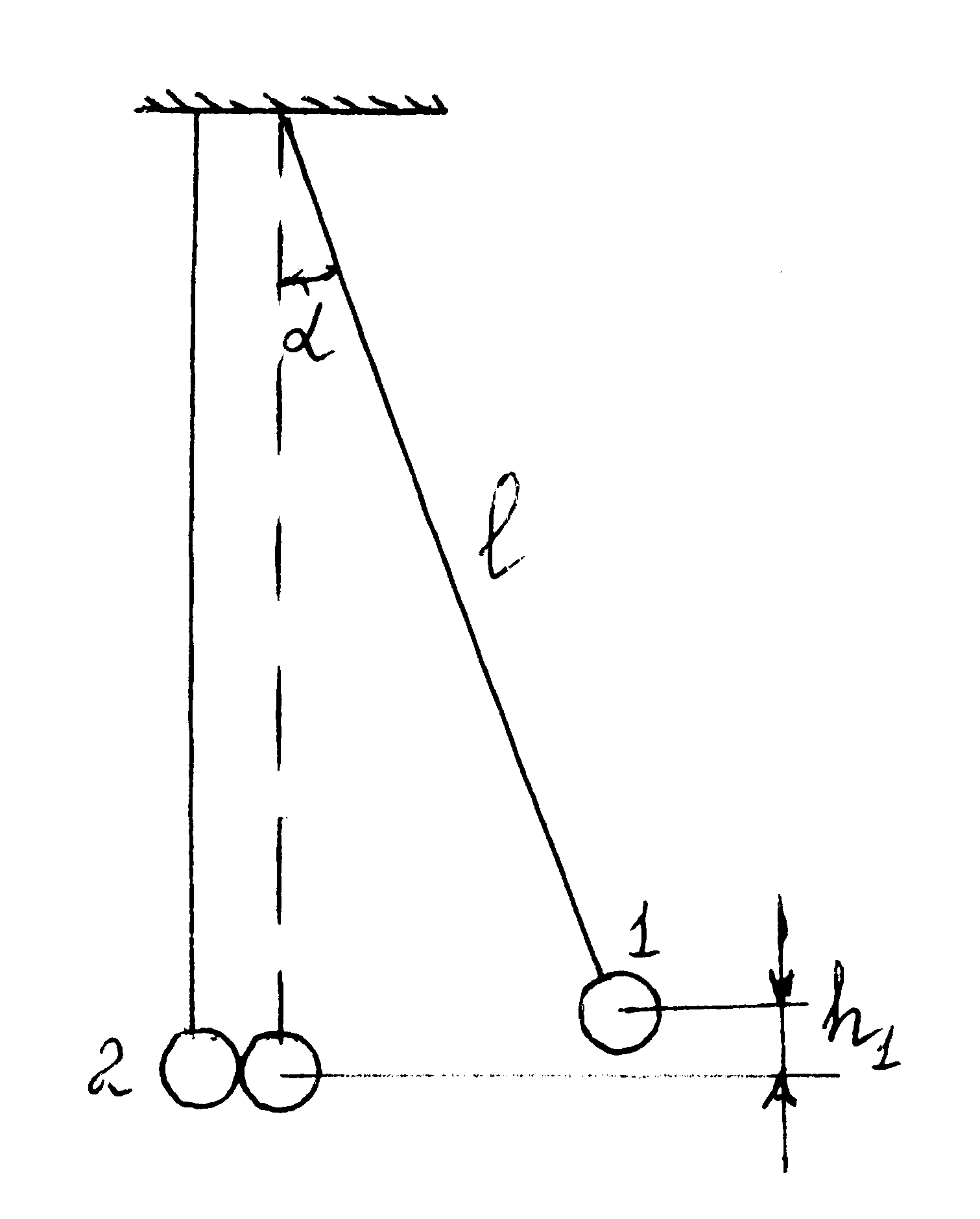 Рис. 35
Рис. 35
 (5-5)
(5-5)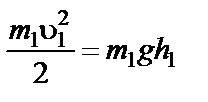
 (5-6)
(5-6) . После преобразования получим
. После преобразования получим .
. Рис. 36
Рис. 36
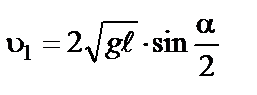 . (5-7)
. (5-7)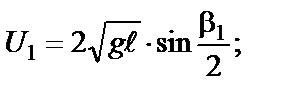 (5-8)
(5-8) (5-9)
(5-9) Рис. 37
Рис. 37
 занесите в табл. 19. Запишите в табл. 20 значения массы шариков m1 и m2 (из табл. 18).
занесите в табл. 19. Запишите в табл. 20 значения массы шариков m1 и m2 (из табл. 18). , м
, м
 для каждого угла по средним значениям скоростей: Р = mu. Результаты вычислений занесите в табл. 20.
для каждого угла по средним значениям скоростей: Р = mu. Результаты вычислений занесите в табл. 20.
 ,
,

 ,
,  ,
,
 , Дж
, Дж
 , Дж
, Дж
 Дж
Дж
 с импульсом первого шара (Р1) до удара. Сделайте вывод.
с импульсом первого шара (Р1) до удара. Сделайте вывод. до и после удара и кинетическую энергию
до и после удара и кинетическую энергию  второго шара после удара для каждого угла a (по средним значениям соответствующих скоростей):
второго шара после удара для каждого угла a (по средним значениям соответствующих скоростей):  . Найдите суммарные энергии до и после удара и сравните их. Результаты занесите в табл. 20. Сделайте вывод.
. Найдите суммарные энергии до и после удара и сравните их. Результаты занесите в табл. 20. Сделайте вывод.