Общие сведения о преобразовании схем

Однотипные элементы электрической цепи соединенные последовательно или параллельно можно заменить одним общим (эквивалентным) элементом. Под "эквивалентным элементом" подразумевается тот факт, что замена не повлияет на величину токов и напряжений в остальной части схемы. Значение параметров эквивалентного элемента определяются исходя из свойств каждого соединения. Подобное преобразование соединений элементов осуществляют для упрощения электрической схемы, а следовательно и упрощения решения электротехнической задачи.

Последовательное соединение элементов

Соединение элементов электрической цепи называют последовательным, если через них протекает один и тот же ток. При последовательном соединении условный конец первого элемента электрической цепи соединяют с условным началом второго элемента, конец второго - с началом третьего и т. д. Ниже на рисунке наглядно отображены принципы преобразования двух и более элементов электрической цепи соединенных последовательно в один эквивалентный.

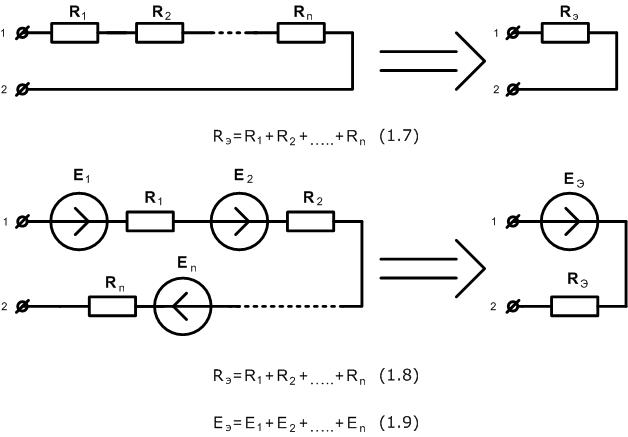
По приведенным в рисунке формулам следует сделать только одно замечание. Если в соотношениях 1.7 и 1.8 имеет место арифметической суммирование величин сопротивлений (т.е. все сопротивления суммируются), то уже в 1.9 имеем дело с алгебраическим суммированием. Некоторые слагаемые могут принимать отрицательные значения, если имеют обратное направление ЭДС. Направление ЭДС источника напряжения определяется по направлению стрелки в условном графическом изображении.

Параллелное соединение элементов

Соединение нескольких элементов называют параллельным, если напряжение на каждом из элементов имеет одно и то же значение. Более наглядно паралленьное соединение элементов отражено на рисунке ниже.

Так же заметим, что в соотношениях 1.10 и 1.11 имеет место арифметическое суммирование, а в 1.12 алгебраическое.

Смешанное соединение элементов

Смешанное соединение элементов представляет собой сочетание рассмотренных последовательного и параллельного соединений. В каждом конкретном случае следует выделять элементы соединенные последовательно или параллельно и по известным формулам заменять их эквивалентными элементами электрической цепи. Таким образом можно существенно упростить схему, а следовательно, и сам расчет электрической цепи. Более наглядно изложенные выше принципы отражены на рисунке.

Типичные решенные задачи, связанные с преобразованием смешанных соединений элементов электрической цепи, приведены в примере №1 и примере №2.

Преобразование соединений треугольник и звезда

Иногда встречаются такие соединения нескольких элементов электрической цепи, в которых нет возможности выделить последовательное или параллельное соединение. Когда заходит разговор про подобные цепи, как правило, вспоминается мостовая схема. Пример схемы мостовой цепи изображен на рисунке ниже.

В таких случаях необходимо выполнить преобразование элементов соединенных по схеме звезда или треугольник. Это преобразование само по себе не является упрощением схемы (количество элементов цепи не меняется), однако приводит схему к виду в котором уже можно выделить последовательные или параллельные соединения элементов, а следовательно, упростить последующими преобразованиями.

Решенная задача, связанная с преобразованием элементов схемы звезда и треугольник приведена в примере №3.

Закон Ома

Данный закон очень удобно применять для ветви электрической цепи. Позволяет определить ток ветви при известном напряжении между узлами, к которым данная ветвь подключена. Также позволяет буквально в одно действие рассчитать одноконтурную электрическую цепь.

При применении закона Ома предварительно следует выбрать направление тока в ветви. Выбор направления можно осуществить произвольно. Если при расчете будет получено отрицательное значение, то это значит, что реальное направление тока противоположно выбранному.

Для ветви, состоящей только из резисторов и подключенной к узлам электрической цепиa и b (см. рис.) закон Ома имеет вид:

Соотношение (1.15) написано в предположении, что выбрано направление тока в ветви от узла a к узлу b. Если мы выберем обратное направление, то числитель будет иметь вид: (U_b-U_a). Теперь становится понятно, что если в соотношении (1.15) возникнет ситуация, когда U_b>U_a то получим отрицательное значение тока ветви. Как уже упоминалось выше, это значит, что реальное направление тока противоположно выбранному. Примером практического применения данного частного случая закона Ома при расчетах электрических цепей является соотношение (1.18) для электрической цепи, изображенной на рисунке.

Для ветви содержащей резисторы и источники электрической энергии закон Ома принимает следующий вид:

Соотношение (1.16) написано в предположении, что предварительно выбрано напавление тока от узла a к узлу b. При расчете алгебраической суммы ЭДС ветви следует знак "+" присваивать тем ЭДС, чье направление совпадает с направлением выбранного тока ветви (направление ЭДС определяется направлением стрелки в обозначении источника электрической энергии). Если направления не совпадают, то ЭДС берется со знаком "-". На рисунке есть примеры применения данного варианта закона Ома - соотношения (1.17) и (1.19)

Если необходимо рассчитать одноконтурную электрическую цепь с произвольным количеством источников электрической энергии и резисторов, то следует применять соотношение (1.16), имея ввиду что U_a=U_b.

Первый закон Кирхгофа

Данный закон применим к любому узлу электрической цепи.

Первый закон Кирхгофа - алгебраическая сумма всех токов, сходящихся в узле равна нулю.

Токи, наравленные к узлу, условно принимаются положительными, а направленные от него - отрицательными (или наоборот). На рисунке ниже изображен пример применения первого закона Кирхгофа для узла, в котором сходится 5 ветвей.

Более понятна для понимания другая формулировка первого закона Кирхгофа: сумма токов, направленных к узлу электрической цепи равна сумме токов, направленных от него.

Второй закон Кирхгофа

Данный закон применим к любому замкнутому контуру электрической цепи.

Второй закон Кирхгофа - в любом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений в отдельных сопротивлениях.

Для применения данного закона на практике, сначала необходимо выбрать замкнутый контур электрической цепи. Далее в нем произвольно выбирают направление обхода (по часовой стрелке, или наоборот). При записи левой части равенства ЭДС, направления которых совпадают с выбранным направлением обхода, принимаются положительными, в обратном случае - отрицательными. При записи правой части равенства положительными считают падения напряжения в тех сопротивлениях, в которых выбранное положительное направление тока совпадает с направлением обхода. В противном случае, падению напряжения следует присвоить знак "минус".На рисунке ниже наглядно представлены примеры составления равенств для нескольких контуров электрической цепи.
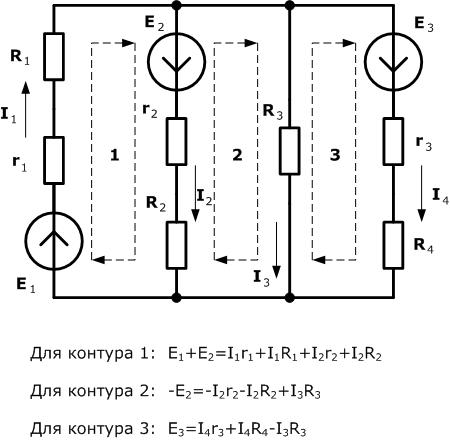