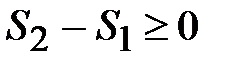|
|
Обратимые и необратимые процессыМомент импульса Определение. Моментом импульса материальной точки относительно точки О называется векторное произведение радиуса-вектора
 перпендикулярно плоскости, в которой лежат векторы перпендикулярно плоскости, в которой лежат векторы  и и  , в соответствии с правилом правого винта, например момент импульса электрона, двигающегося по круговой орбите в боровской модели атома. , в соответствии с правилом правого винта, например момент импульса электрона, двигающегося по круговой орбите в боровской модели атома.
Свяжем момент импульса с моментом инерции и угловой скоростью. Пусть радиус-вектор
5. Уравнение моментов. Уравнение моментов (оно связывает момент импульса с моментом силы).
Производная по времени момента импульса материальной точки относительно точки О равна моменту действующей силы относительно точки О. Уравнение динамики вращательного движения твёрдого тела Относительно неподвижной оси В проекции на ось
а так как
Замечание: если вокруг оси
(Угловое ускорение Закон сохранения импульса.
Закон сохранения импульса Импульс изолированной системы не изменяется при любых процессах, протекающих внутри системы. Закон сохранения импульса связан с однородностью пространства: параллельный перенос замкнутой системы с одного места пространства в другое, поставив при этом все тела в те же условия (без изменения расположения и скоростей), в каких они находились в прежнем положении, не отразится на ходе всех последующих явлений.
Дляизолированной системы Закон сохранения момента импульса: момент импульса замкнутой системы частиц остаётся постоянным. Если система движется в поле силы тяжести Земли, то легко показать, что относительно любой вертикальной осимомент силы тяжести равен нулю и закон сохранения момента импульса выполняется в проекции на вертикальную ось, т.е.
Закон сохранения механической энергии.
Закон сохранения механической энергии: полная механическая энергия замкнутой системы частиц, на которую действуют только консервативные силы, остаётся постоянной в процессе движения системы. В основе закона сохранения энергии лежит однородность времени, которая означает, что если в два любых момента времени все тела замкнутой системы поставить в совершенно одинаковые условия, то, начиная с этих моментов, все явления в ней будут протекать совершенно одинаково 7. Уравнение неразрывности. - для несжимаемой жидкости при стационарном течении произведение
Это утверждение носит название теоремы о неразрывности струи. Она применима даже к газам, если их сжимаемостью можно пренебречь (
Уравнение Бернулли
Заметим, что уравнение вполне строго лишь при
Уравнение выражает для движущейся жидкости закон сохранения механической энергии. Для горизонтальной линии тока:
8. Циркуляция скорости. Рассмотрим поле скоростей жидкости Пусть Н.Е. Жуковский (выдающийся русский механик, уроженец Владимирской губернии (1847 – 1921)) впервые установил вихревую природу сил, действующих со стороны потока на крыло, и указал на наличие простой зависимости между силой и циркуляцией скорости по контуру, охватывающему обтекаемое идеальной несжимаемой жидкостью крыло (рис. 5.9). Рис. 5.9 Сверху профиль крыла выпуклый, линии тока сверху крыла сгущаются, сечение потока уменьшается, скорость больше, чем снизу, где профиль плоский. Циркуляция скорости потока по контуру профиля крыла оказывается отличной от нуля. Согласно формуле Жуковского возникает подъёмная сила на единицу длины крыла:
где 9. Принцип относительности Эйнштейна. Классическая механика, основанная на законах Ньютона, справедлива только для тел, движущихся со скоростями, много меньшими скорости света в пустоте ( В основе теории лежит принцип относительности, состоящий из двух постулатов: 1. Постулат относительности. Все законы природы и уравнения, их описывающие, инвариантны, т.е. не меняются при переходе от одной инерциальной системы отсчёта к другой (Замечание: неизменность вида уравнений при замене координат и времени одной системы отсчёта координатами и временем другой системы называется инвариантностью). 2. Постулат постоянства скорости света. Скорость света в вакууме не зависит от движения источника и приёмника света и одинакова во всех направлениях, т.е. скорость света в вакууме одинакова во всех инерциальных системах отсчёта. Лоренцево сокращение длины.
или Так как Таким образом, длина стержня, измеренная в системе, относительно которой он движется Замедление времени
Так как Время
2 раздел: основы молекулярной физики и термодинамики! Понятие идеального газа. 1. Идеальным называется газ, взаимодействие, между молекулами которого пренебрежимо мало и состояние которого описывается уравнением Клапейрона-Менделеева. Основное уравнение молекулярно-кинетической теории. Постановка задачи. Требуется получить связь между макропараметрами – давлением P, температурой T, с микропараметрами – массой молекулы m, её скоростью
Физический смысл уравнения: давление, оказываемое газом на стенки сосуда прямо пропорциональна числу молекул в единице объёма и средней кинетической энергии поступательного движения одной молекулы. Уравнение состояния идеального газа Клапейрона-Менделеева Количество вещества 2. Распределение Максвелла(английский физик 1831-1879). Скорости каждой молекулы в пространстве скоростей соответствует точка. Распределение этих точек в Барометрическая формула. Атмосферное давление на высоте h обусловлено весом вышележащих слоёв газа. Давление на высоте h+dh будет P+dP (dh>0, dP<0, т.к. вес и давление с высотой убывают). Разность давлений P и P+dP обусловлена весом газа, заключённого в объёме цилиндра, с площадью основания, равной При нормальных условиях воздух можно считать идеальным газом. Для случая, когда температура постоянная (изотермическая атмосфера), получим:
Распределение Больцмана Из барометрической формулы в результате подстановок и сокращений получим распределение концентрации молекул по высоте в поле силы тяжести Земли.
Из этой формулы следует, что с понижением температуры число частиц на высотах, отличных от нуля, убывает обращаясь в 0 при Т=0 (при абсолютном нуле все молекулы расположились бы на поверхности Земли). При высоких температурах n слабо убывает с высотой, так что молекулы оказываются распределёнными по высоте почти равномерно. Распределение молекул по высоте является результатом конкуренции между притяжением молекул к Земле и тепловым движением, стремящимся разбросать молекулы по всем высотам. На разной высоте молекула обладает различным запасом потенциальной энергии
Таким образом, закон Больцмана (*) даёт распределение частиц, находящихся в состоянии хаотического теплового движения, по значениям потенциальной энергии. 3. Уравнение Ван-дер-Ваальса Сила взаимодействия между двумя элементарными объёмами пропорциональна плотности молекул, заключённых в одном и другом объёмах
- уравнение Ван-дер-Ваальса. Здесь a и b – постоянные Ван-дер-Ваальса, для разных газов они имеют свои значения. Изотермы реального газа Эти кривые рассматриваются для четырёх различных температур. При высоких температурах
при температурах 2. Метастабильные состояния (греч. meta – после, за, в данном случае за стабильным состоянием, неустойчивые состояния). Рассмотрим часть изотермы
( Эффект Джоуля-Томсона Эффект Джоуля – Томсона заключается в изменении температуры газа в результате адиабатического дросселирования – медленного протекания газа под действием постоянного перепада давления через дроссельное препятствие (например, пористую перегородку Др - дроссель на рис. 9.4). Термин «адиабатическое» означает без теплообмена с окружающей средой. Адиабатичность может быть осуществлена, например, с помощью теплоизолирующей оболочки вокруг канала. При
между молекулами. При расширении молекулы газа совершают работу против сил притяжения и температура уменьшается. При этом кинетическая энергия теплового движения газа расходуется на работу против сил молекулярного притяжения. Сжижение газов Газ может быть превращён в жидкое состояние, если его температура ниже критической и ниже температуры кипения при данном давлении. Атмосферный воздух сжимается компрессором (К) до давления 220 атм. Сжатый воздух проходит по трубопроводу и охлаждается проточной водой до 10
4. Основные термодинамические понятия Термодинамика рассматривает явления, опираясь на основные законы (начала), которые являются обобщением огромного количества опытных данных. Внутренняя энергия– энергия физической системы, зависящая от её внутреннего состояния. Внутренняя энергия включает энергию хаотического (теплового) движения всех микрочастиц системы (молекул, атомов, ионов и т.д.) и энергию взаимодействия этих частиц. Внутренняя энергия – функция состояния системы. Работа термодинамической системы над внешними телами заключается в изменении состояния этих тел и определяется количеством энергии, передаваемой системой внешним телам при изменении объема. Теплота (количество теплоты) – количество энергии, получаемой или отдаваемой системой при теплообмене. Элементарное количество теплоты 1-ый закон (начало) термодинамики: количество теплоты, сообщённое системе, идёт на приращение внутренней энергии системы и на совершение системой работы над внешними телами.
где
5. Теплоёмкостью
Размерность теплоёмкости тела 1. Рассмотрим нагревание газа при постоянном объёме. По первому закону термодинамики:
Тогда
2. Теплоёмкость газа при постоянном давлении:
Для идеального газа для 1 моля (из уравнения Менделеева-Клапейрона).
Продифференцируем это выражения по температуре Т, получим:
3. При адиабатическом процессе (процесс протекающий без теплообмена с внешней средой).
4. При изотермическом процессе Существуют процессы, при которых газ, расширяясь, совершает работу большую, чем полученная теплота, тогда его температура понижается, несмотря на приток теплоты. Теплоёмкость в этом случае отрицательна. В общем случае
Обратимые и необратимые процессы Процесс называется обратимым, если возможно осуществить обратный переход из В в А через те же промежуточные состояния, что и в прямом процессе, чтобы не осталось никаких изменений и в самом теле и в окружающих телах. Если же обратный процесс невозможен, или по окончании процесса в окружающих телах и в самом теле остались какие-либо изменения, то процесс являетсянеобратимым. Примеры необратимых процессов. Любой процесс сопровождаемый трением является необратимым (теплота, выделяющаяся при трении не может без затраты работы другого тела собраться и вновь превратиться в работу). Все процессы, сопровождаемые теплопередачей от нагретого тела к менее нагретому, является необратимыми (например, теплопроводность). К необратимым процессам также относятся диффузия, вязкое течение. Все необратимые процессы являются неравновесными. Равновесные – это такие процессы, которые представляют из себя последовательность равновесных состояний. Равновесное состояние – это такое состояние, в котором без внешних воздействий тело может находиться сколь угодно долго. Круговой процесс (цикл). Если тело из состояния А в состояние В переходит через одни промежуточные состояния, а возвращается в начальное состояние А через другие промежуточные состояния, то совершается круговой процесс, или цикл.
2. Цикл Карно и его КПД для идеального газа Рабочий цикл состоит из двух равновесных изотерм и двух равновесных адиабат (рис. 15.2). В машине, как допускают, отсутствуют потери на трение, теплопроводность и т.д. С машиной связаны два резервуара теплоты. Один, имеющий температуру Цикл Карно заключается в следующем. Сначала система, имея температуру
Рассчитаем коэффициент полезного действия идеальной тепловой машины, работающей по циклу Карно. Эта величина равна отношению количества теплоты, превращённого в работу, к количеству теплоты, полученному от нагревателя.
Полезная работа за цикл равна сумме всех работ отдельных частей цикла:
Работа изотермического расширения:
адиабатического расширения:
изотермического сжатия:
адиабатического сжатия:
То есть КПД цикла Карно определяется только температурами нагревателя и холодильника. Принцип действия теплового двигателя и холодильной машины Любой тепловой двигатель состоит из 3-х основных частей: рабочего тела, нагревателя и холодильника. Рабочее тело получает некоторое количество теплоты
Холодильная машина. Цикл Карно обратим, следовательно, его можно провести в обратном направлении. (4-3-2-1-4 (рис.15.3)) От холодильной камеры поглощается тепло
электрической сети. За счёт этой энергии и совершается процесс “передачи теплоты” от холодильной камеры к более нагретым телам (к окружающей среде). 7. Энтропия. Закон возрастания энтропии Из статической физики: отношение количества теплоты Закон возрастания энтропии. Допустим, что изолированная система переходит из равновесного
(для обратного процесса знак “=” , для необратимого “<”). Для нашего перехода 1 – 2 – 1 :
Так как процесс 2 – 1 обратимый, то будет равенство
Под температурой Если система адиабатически изолирована, то
Таким образом, энтропия адиабатически изолированной системы не может убывать, она либо возрастает, либо остаётся постоянной. (Закон возрастания энтропии). |
|
 :
:
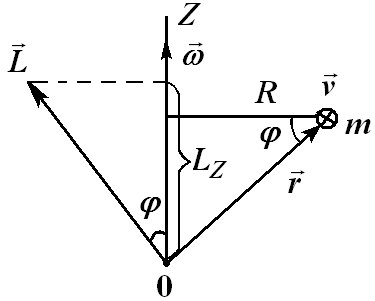 Рис. 3.10
Рис. 3.10
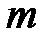 лежит в плоскости рис. 3.10, скорость
лежит в плоскости рис. 3.10, скорость 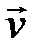 перпендикулярна ей («от нас»), частица движется по окружности радиусом
перпендикулярна ей («от нас»), частица движется по окружности радиусом  .
.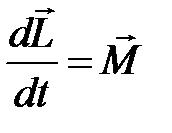
 предыдущее уравнение запишется:
предыдущее уравнение запишется: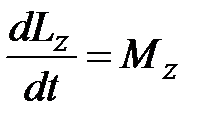
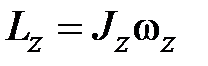 , то
, то  , если
, если  , то
, то  . Так как
. Так как 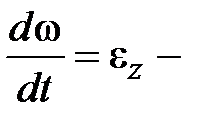 проекция углового ускорения на ось
проекция углового ускорения на ось 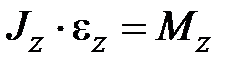



 , и тогда очевидно:
, и тогда очевидно:
 совпадает по направлению с вектором момента силы).
совпадает по направлению с вектором момента силы).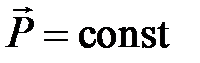

 (
( 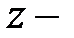 вертикальная ось), и соответственно:
вертикальная ось), и соответственно:

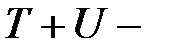 полная механическая энергия системы.
полная механическая энергия системы. в любом сечении данной трубки тока имеет постоянное значение:
в любом сечении данной трубки тока имеет постоянное значение: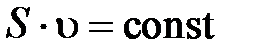
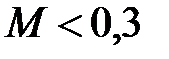 ). Примеры: 1) в узком месте река течёт быстро, в широком – медленно; 2) пожарный брандспойт имеет сужающийся наконечник, чтобы скорость воды была больше и струя летела дальше.
). Примеры: 1) в узком месте река течёт быстро, в широком – медленно; 2) пожарный брандспойт имеет сужающийся наконечник, чтобы скорость воды была больше и струя летела дальше.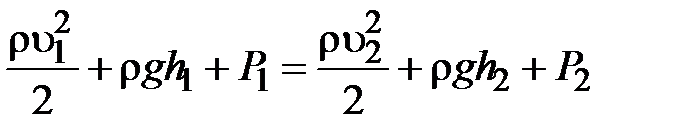
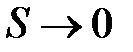 , т.е. для одной и той же линии тока. Так как
, т.е. для одной и той же линии тока. Так как  и
и 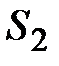 были выбраны произвольно, то можно утверждать, что для любой линии тока в стационарно текущей идеальной и несжимаемой жидкости выполняется условие (уравнение Бернулли):
были выбраны произвольно, то можно утверждать, что для любой линии тока в стационарно текущей идеальной и несжимаемой жидкости выполняется условие (уравнение Бернулли):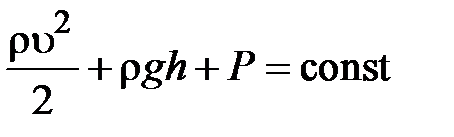

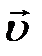 . В этом поле возьмём произвольный замкнутый контур L (рис. 5.8).
. В этом поле возьмём произвольный замкнутый контур L (рис. 5.8).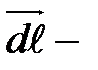 элемент длины контура. Интеграл
элемент длины контура. Интеграл  называется циркуляцией вектора скорости по контуру L. Если циркуляция скорости по любому замкнутому контуру, охватывающему обтекаемое тело, равна нулю, то движение жидкости (газа) называется потенциальным. В противном случае движение называется вихревым.
называется циркуляцией вектора скорости по контуру L. Если циркуляция скорости по любому замкнутому контуру, охватывающему обтекаемое тело, равна нулю, то движение жидкости (газа) называется потенциальным. В противном случае движение называется вихревым.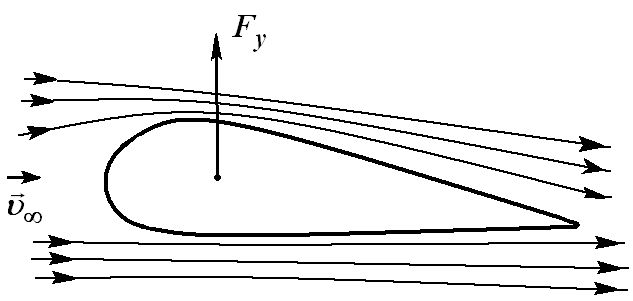
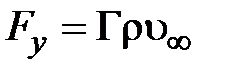
 и
и 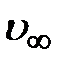 соответственно плотность потока и скорость невозмущённого крылом потока.
соответственно плотность потока и скорость невозмущённого крылом потока. ). Для описания движений, совершающихся со скоростями, сравнимыми со скоростью света, Эйнштейн создал релятивистскую механику (relativus (лат.) – относительный). Различают специальную (являющуюся предметом нашего рассмотрения) и общую теорию относительности. Специальная означает рассмотрение явлений в инерциальных системах отсчёта.
). Для описания движений, совершающихся со скоростями, сравнимыми со скоростью света, Эйнштейн создал релятивистскую механику (relativus (лат.) – относительный). Различают специальную (являющуюся предметом нашего рассмотрения) и общую теорию относительности. Специальная означает рассмотрение явлений в инерциальных системах отсчёта. ,
,
 , то
, то  .
. , оказывается меньше длины
, оказывается меньше длины  , измеренной в системе, относительно которой стержень покоится. Это явление называется лоренцевым сокращением длины.
, измеренной в системе, относительно которой стержень покоится. Это явление называется лоренцевым сокращением длины.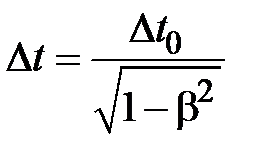
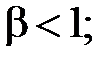
 , тогда
, тогда  .
.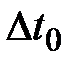 , отсчитываемое по часам, движущимся вместе с телом, называется собственным временем тела. Таким образом, время, отсчитанное по часам, относительно которых система движется, всегда больше собственного времени (замедление времени).
, отсчитываемое по часам, движущимся вместе с телом, называется собственным временем тела. Таким образом, время, отсчитанное по часам, относительно которых система движется, всегда больше собственного времени (замедление времени). и концентрацией молекул n.
и концентрацией молекул n.
 можно представить в виде отношения массы газа m к молярной массе газа М
можно представить в виде отношения массы газа m к молярной массе газа М 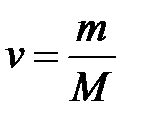 и окончательно уравнение состояния идеального газа (уравнение Клапейрона-Менделеева) для массы газа m:
и окончательно уравнение состояния идеального газа (уравнение Клапейрона-Менделеева) для массы газа m: 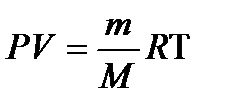
 пространстве характеризует распределение молекул по скоростям. Вследствие равноправности всех направлений движения, расположение точек относительно начала координат будет сферически симметричным. Плотность точек в
пространстве характеризует распределение молекул по скоростям. Вследствие равноправности всех направлений движения, расположение точек относительно начала координат будет сферически симметричным. Плотность точек в  пространстве будет зависеть только от модуля скорости
пространстве будет зависеть только от модуля скорости 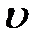 . Для скоростей, лежащих в пределах от
. Для скоростей, лежащих в пределах от  до
до 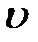 +d
+d  пространстве
пространстве 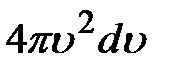 (объём сферического слоя). Число точек, находящихся в этом слое (каждая точка соответствует скорости отдельной молекулы)
(объём сферического слоя). Число точек, находящихся в этом слое (каждая точка соответствует скорости отдельной молекулы) 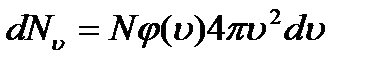 , где
, где  плотность точек в
плотность точек в  пространстве (подобно тому, как из выражения следует
пространстве (подобно тому, как из выражения следует  ). Смысл
). Смысл 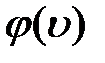 далее.
далее.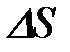 и высотой dh
и высотой dh , отсюда получаем барометрическую формулу:
, отсюда получаем барометрическую формулу: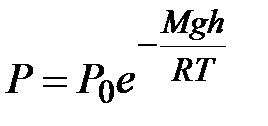

 .Следовательно, распределение молекул по высоте является и распределением их по значениям потенциальной энергии.
.Следовательно, распределение молекул по высоте является и распределением их по значениям потенциальной энергии.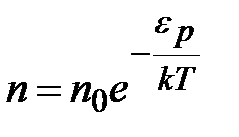
 . Плотность – величина, обратная объёму, занимаемому молекулами.
. Плотность – величина, обратная объёму, занимаемому молекулами. 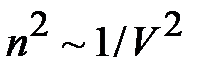 . Отсюда поправка на взаимодействие молекул
. Отсюда поправка на взаимодействие молекул 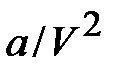 , где a – некоторая константа, характеризующая силы молекулярного притяжения. В результате уравнение состояния одного моля реального газа приняло вид:
, где a – некоторая константа, характеризующая силы молекулярного притяжения. В результате уравнение состояния одного моля реального газа приняло вид:
 изотерма реального газа отличается от изотермы идеального газа только некоторым искажением её формы, оставаясь монотонно спадающей кривой. При некоторой температуре
изотерма реального газа отличается от изотермы идеального газа только некоторым искажением её формы, оставаясь монотонно спадающей кривой. При некоторой температуре  на изотерме имеется точка перегиба К. Эта изотерма называется критической, соответствующая ей температура
на изотерме имеется точка перегиба К. Эта изотерма называется критической, соответствующая ей температура  называется критическим состоянием.
называется критическим состоянием.
 изотермы имеют волнообразный участок. У реальных изотерм такого завитка нет, вместо него у них имеется прямолинейный горизонтальный участок (на рис. 9.2 обозначены пунктиром). Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая, ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму P, V под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар Ж+П), слева от неё находится область жидкого состояния (Ж), а справа – область пара (П). Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращён в жидкость ни при каком давлении.
изотермы имеют волнообразный участок. У реальных изотерм такого завитка нет, вместо него у них имеется прямолинейный горизонтальный участок (на рис. 9.2 обозначены пунктиром). Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая, ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму P, V под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар Ж+П), слева от неё находится область жидкого состояния (Ж), а справа – область пара (П). Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращён в жидкость ни при каком давлении.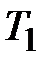 рис. 9.3. Состояния на участке 2-3 не реализуются, т.к. на нём
рис. 9.3. Состояния на участке 2-3 не реализуются, т.к. на нём  , т.е. увеличение объёма газа сопровождалось бы не уменьшением, а ростом давления – совершенно противоестественное свойство. На участках 1-2 и 3-4
, т.е. увеличение объёма газа сопровождалось бы не уменьшением, а ростом давления – совершенно противоестественное свойство. На участках 1-2 и 3-4 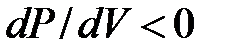 , это нормально, но оказывается, что эти состояния не вполне устойчивы. Достаточно в состоянии А попадание в пар пылинки, чтобы вещество распалось на две фазы и перешло в состояние В. (Напомним, что фазой называется однородная, одинаковая по свойствам часть системы. Например, в закрытом сосуде вода и смесь воздуха и паров воды. Пар, находящийся вравновесии со своей жидкостью называетсянасыщенным.
, это нормально, но оказывается, что эти состояния не вполне устойчивы. Достаточно в состоянии А попадание в пар пылинки, чтобы вещество распалось на две фазы и перешло в состояние В. (Напомним, что фазой называется однородная, одинаковая по свойствам часть системы. Например, в закрытом сосуде вода и смесь воздуха и паров воды. Пар, находящийся вравновесии со своей жидкостью называетсянасыщенным.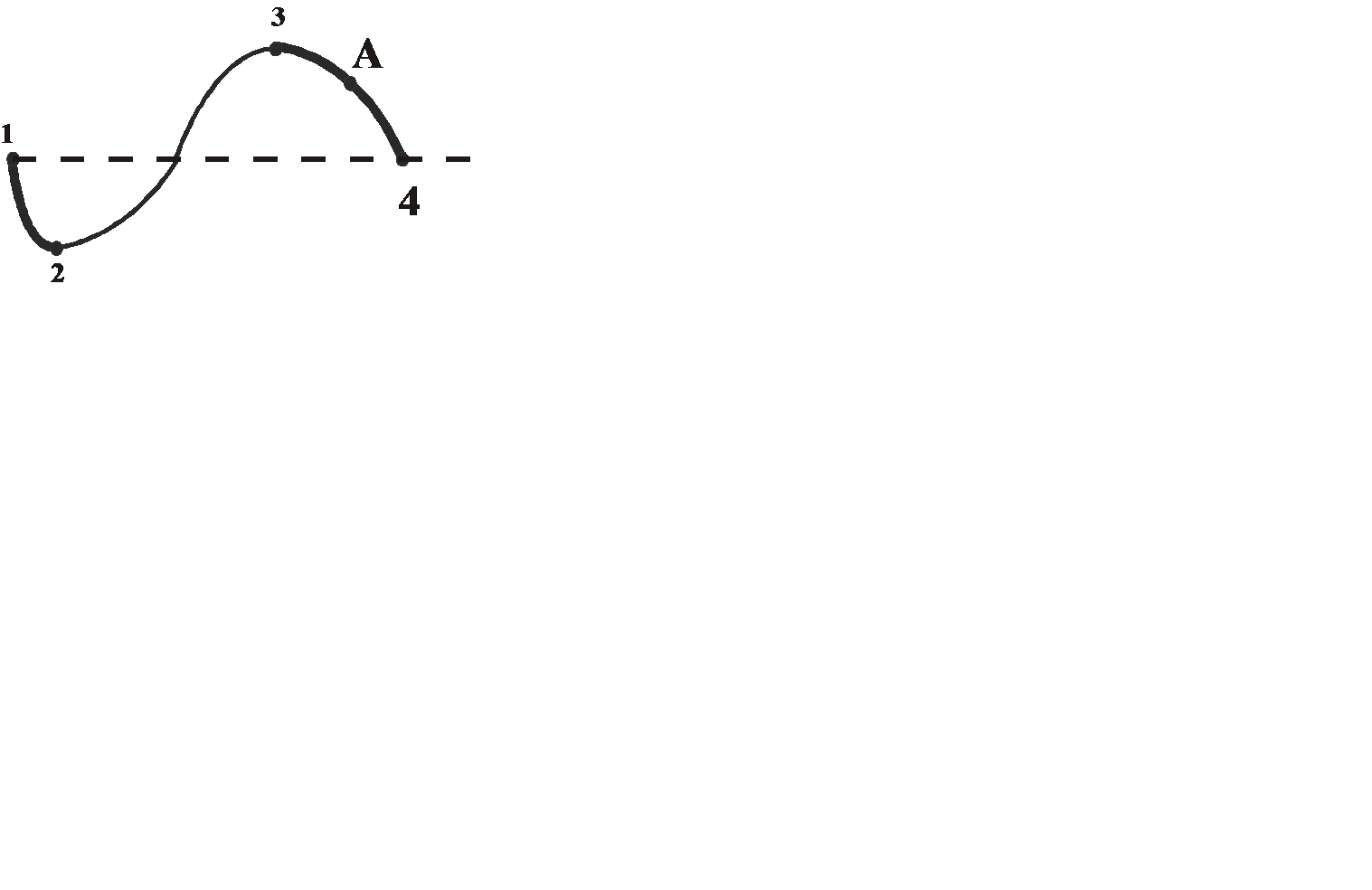
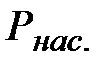 ). Состояния, подобные состоянию А (неустойчивые) называются метастабильными. Состояние 1-2, где давление меньше
). Состояния, подобные состоянию А (неустойчивые) называются метастабильными. Состояние 1-2, где давление меньше  ) – пересыщенным паром.
) – пересыщенным паром.
 (
(  ). Различают а) положительный эффект для Т, когда температура реального газа понижается
). Различают а) положительный эффект для Т, когда температура реального газа понижается  и б) отрицательный эффект, когда
и б) отрицательный эффект, когда  (для идеального газа T=const). Практический интерес представляет положительный эффект. Положительный эффект наблюдается в области давлений, где преобладают силыпритяжения
(для идеального газа T=const). Практический интерес представляет положительный эффект. Положительный эффект наблюдается в области давлений, где преобладают силыпритяжения
 15
15  . Далее воздух поступает во внутренний канал змеевика откуда в резервуар (Р), где давление 20 атм. При этом воздух охлаждается на 50
. Далее воздух поступает во внутренний канал змеевика откуда в резервуар (Р), где давление 20 атм. При этом воздух охлаждается на 50  При температуре 180
При температуре 180  не является в общем случае дифференциалом какой-либо функции параметров состояния. Передаваемое системе количество теплоты, как и работа, зависит от того, каким способом система переходит из начального состояния в конечное.
не является в общем случае дифференциалом какой-либо функции параметров состояния. Передаваемое системе количество теплоты, как и работа, зависит от того, каким способом система переходит из начального состояния в конечное.
 количество сообщённой телу теплоты;
количество сообщённой телу теплоты; и
и  начальное и конечное значения внутренней энергии;
начальное и конечное значения внутренней энергии;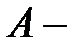 работа, совершённая системой над внешними телами.
работа, совершённая системой над внешними телами. тела называется величина, равная отношению сообщённого телу количества теплоты
тела называется величина, равная отношению сообщённого телу количества теплоты  к соответствующему приращению температуры
к соответствующему приращению температуры  .
.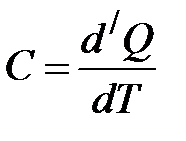
 .
.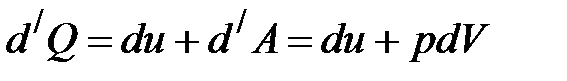 , т.к.
, т.к.  , то
, то 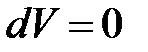 .
.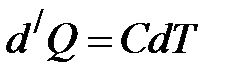 по определению, а для процесса с
по определению, а для процесса с 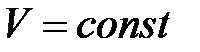 :
: , где
, где теплоёмкость газа при постоянном объёме.
теплоёмкость газа при постоянном объёме.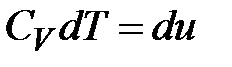 и
и
 .
. .
. , получим для 1 моля
, получим для 1 моля
 ,
,  , т.е. теплоёмкость в адиабатическом процессе равна нулю.
, т.е. теплоёмкость в адиабатическом процессе равна нулю. ,
,  , и, следовательно, теплоёмкость
, и, следовательно, теплоёмкость 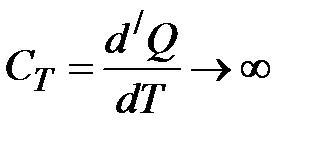 .
. .
.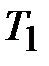 , называется нагревателем, другой имеющий более низкую температуру
, называется нагревателем, другой имеющий более низкую температуру  – холодильником (или теплоприёмником). Резервуары настолько велики, что отдача или получение теплоты не изменяет их температуру.
– холодильником (или теплоприёмником). Резервуары настолько велики, что отдача или получение теплоты не изменяет их температуру. , приводится в тепловой контакт с нагревателем. Затем, бесконечно медленно уменьшая внешнее давление, её заставляют расширяться по изотерме 1-2. При этом она получает тепло
, приводится в тепловой контакт с нагревателем. Затем, бесконечно медленно уменьшая внешнее давление, её заставляют расширяться по изотерме 1-2. При этом она получает тепло 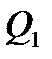 от нагревателя и производит работу
от нагревателя и производит работу 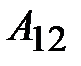 против внешнего давления. После этого систему адиабатически изолируют и заставляют расширяться по адиабате 2 – 3, пока её температура не достигает температуры холодильника
против внешнего давления. После этого систему адиабатически изолируют и заставляют расширяться по адиабате 2 – 3, пока её температура не достигает температуры холодильника 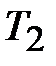 . При адиабатическом расширении система также совершает некоторую работу против внешнего давления. В состоянии 3 систему приводят в тепловой контакт с холодильником и непрерывным увеличением давления изотермически сжимают её до некоторого состояния 4. При этом над системой производится работа (т.е. сама система совершает отрицательную работу
. При адиабатическом расширении система также совершает некоторую работу против внешнего давления. В состоянии 3 систему приводят в тепловой контакт с холодильником и непрерывным увеличением давления изотермически сжимают её до некоторого состояния 4. При этом над системой производится работа (т.е. сама система совершает отрицательную работу  ), и она отдаёт холодильнику некоторое количество тепла
), и она отдаёт холодильнику некоторое количество тепла  . Состояние 4 выбирается так, чтобы можно было сжатием по адиабате 4 – 1 вернуть систему в исходное состояние. Для этого над системой надо совершить работу
. Состояние 4 выбирается так, чтобы можно было сжатием по адиабате 4 – 1 вернуть систему в исходное состояние. Для этого над системой надо совершить работу 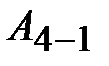 (система должна произвести отрицательную работу
(система должна произвести отрицательную работу  ). В результате кругового процесса Карно внутренняя энергия системы не изменяется, поэтому произведённая работа
). В результате кругового процесса Карно внутренняя энергия системы не изменяется, поэтому произведённая работа 
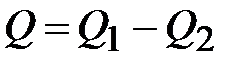
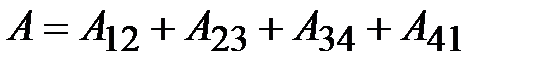 .
.
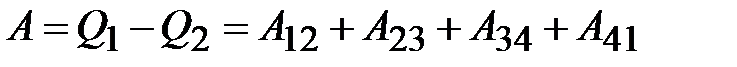 .
. ,
, ,
, ,
,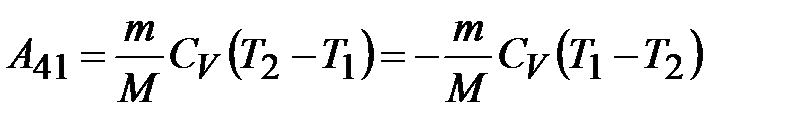 .
.
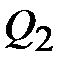 холодильнику. Полученная работа, совершаемая двигателем за цикл:
холодильнику. Полученная работа, совершаемая двигателем за цикл: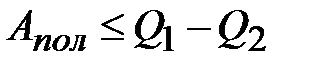
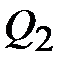 .
.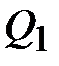 . Внешние силы совершают работу
. Внешние силы совершают работу  , тогда
, тогда
 В результате цикла некоторое количество теплоты переходит от холодного тела к телу с более высокой температурой.
Реально рабочим телом в холодильной установке обычно служат пары легкокипящих жидкостей – аммиак, фреон и т. п. К машине подводится энергия от
В результате цикла некоторое количество теплоты переходит от холодного тела к телу с более высокой температурой.
Реально рабочим телом в холодильной установке обычно служат пары легкокипящих жидкостей – аммиак, фреон и т. п. К машине подводится энергия от
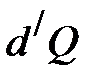 , сообщаемого системе, к температуре
, сообщаемого системе, к температуре  (системы) есть приращение некоторой функции состояния
(системы) есть приращение некоторой функции состояния  (энтропий).
(энтропий). 

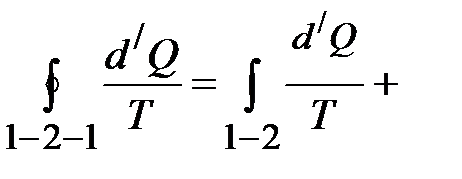
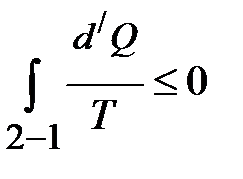 .
.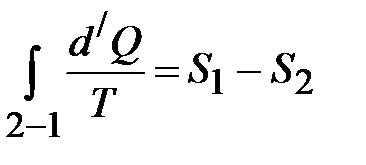 , отсюда
, отсюда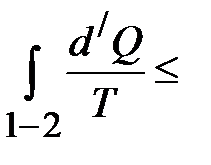
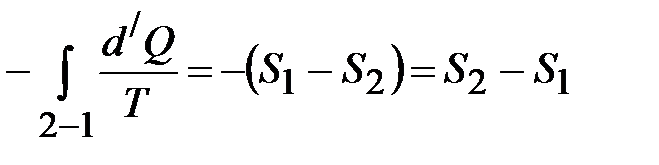 .
.
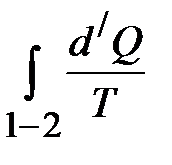
 понимается температура системы, при которой она отдаёт или принимает тепло
понимается температура системы, при которой она отдаёт или принимает тепло  .
. и
и