|
|
Волновое уравнение и его решение.Уравнение, позволяющее определить смещение
(28-1) , где
 , на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны , на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны
Введем величину
 , то получится вектор, называемый волновым вектором , то получится вектор, называемый волновым вектором 
На рис.28.2 представлено графическое изображение волны
Уравнение любой волны является решением дифференциального уравнения, называемого волновым уравнением
Гармоническая волна- волна при которой каждая точка колеблющейся среды или поля в каждой точке пространства совершает гармонические колебания. 4. 5. 6. Система уравнений Максвелла в интегральной и дифференциальной формах. Электромагнитное поле. В законе электромагнитной индукции (ЭМИ) ℇ ℇ =
 = =  Магнитный поток по определению Ф = Магнитный поток по определению Ф =  . Подставляя в закон ЭМИ получим . Подставляя в закон ЭМИ получим
(30-4)
Это первое уравнение Максвелла.
(Поскольку в общем случае
производную Смысл первого уравнения соответствует максвелловской трактовке явления ЭМИ, то есть, изменяющееся со временем магнитное поле порождает вихревое электрическое поле. Второе уравнение Максвелла
(30-5)
Это уравнение выражает тот факт, что силовые линии магнитного поля не имеют источника (нет «магнитных зарядов») и всегда замкнуты и, что оно имеет вихревой характер, поток вектора магнитной индукции равен нулю. Третье уравнение Максвелла
Это обобщенный закон полного тока (см. часть 3, лекция №24), который подчеркивает тот факт, что магнитное поле может создаваться не только токами проводимости ( Четвертая теорема Максвелла (см. часть 3, лекция №18).
(30-7)
Физически эта теорема подчеркивает тот факт, что электрическое поле может создаваться зарядами, то есть источниками силовых линий электрического поля являются электрические заряды. Уравнения (30-3,5,6,7) представляют уравнения Максвелла в интегральной форме. Уравнения Максвелла подчеркивают тот факт, что электрическое поле может создаваться как зарядами, так и переменным магнитным полем, а магнитное поле может создаваться как токами проводимости, так и переменным электрическим полем. При этом магнитное поле всегда носит вихревой характер, о чем говорит второе уравнение Максвелла. Электрическое поле, создаваемое зарядами и переменным магнитным полем носят различный характер.Силовые линии в первом случае начинаются и кончаются на зарядах (четвертое уравнение Максвелла). А электрическое поле, создаваемое переменным магнитным полем не имеет источников и носит вихревой характер, также как магнитное поле (первое уравнение Максвелла). В вакууме, где нет зарядов и токов, магнитное поле может создаваться только переменным электрическим полем, а электрическое поле только переменным магнитным полем. Эту совокупность непрерывно изменяющихся и порождающих друг друга электрического и магнитного полей Максвелл назвал электромагнитным полем. Кроме четырех рассмотренных уравнений в полную систему уравнений Максвелла входят еще три уравнения, называемых материальными. В них входят характеристики вещества («материи»), такие как диэлектрическая и магнитная проницаемости ℰ и µ, проводимость σ.
Связь
Связь
Закон Ома в локальной форме (лекция №20, часть 3)
Уравнения Максвелла (30-4) ÷ (30-7) можно представить в дифференциальной форме, т.е. в виде системы дифференциальных уравнений. Для этого используем теоремы Стокса
(30-8)
и Остроградского – Гаусса:
где Первое уравнение Максвелла
С другой стороны, используя теорему Стокса, получим
Поскольку равны левые части, равны и правые
откуда следует
(30-10)
Второе уравнение Максвелла
С другой стороны из теоремы Остроградского – Гаусса
Третье уравнение запишем, предварительно выразив токи проводимости через плотность токов проводимости
тогда
с другой стороны
получим
(30-12)
Аналогичный подход для четвертого уравнения дает систему уравнений
 - объемная плотность заряда) из которой следует: - объемная плотность заряда) из которой следует:
(30-13)
Сведем четыре уравнения Максвелла в интегральной и дифференциальной формах, а также три материальных уравнения в таблицу: Уравнения Максвелла
Отметим, что физический смысл уравнений в дифференциальной форме такой же, что и соответствующих уравнений в интегральной форме. Интегрируя их, можно получить Примечание.Вихревое электрическое поле характеризуется особой векторной величиной, называемой ротором напряженности поля: По определению
7. где - скорость распространения электромагнитной волны. Процесс распространения электромагнитного поля в пространстве называется электромагнитной волной.
то есть скорость электромагнитной волны в вакууме равна скорости света в вакууме. Это обстоятельство приводит к выводу, что свет - электромагнитная волна. Решения уравнений (30-14)
Выражения (30-15) – уравнения электромагнитной волны. Их графическое
Как показывает опыт, электромагнитные волны проходят через диэлектрики и отражаются от металлов. Для них свойственны такие явления как интерференция, дифракция, поляризация, дисперсия (рассмотрим далее в разделе «Оптика»).
Физика. 5 раздел – оптика! 1. Принцип Гюйгенса устанавливает способ построения фронта волны в момент Каждая точка, до которой доходит волновое движение, служит центром
Законы отражения и преломления. Линии, вдоль которых распространяется световая энергия, называется лучами.В изотропных средах направление распространения световой энергии совпадает с направлением волнового вектора
 ) на на плоскую границу раздела двух однородных и изотропных диэлектриков (рис. 31.2) кроме ) на на плоскую границу раздела двух однородных и изотропных диэлектриков (рис. 31.2) кроме
плоскостью падения волны. Энергия, которую несет с собой падающий луч, распределяется между отраженным и преломленным лучами. На рис. 31.2 ϑ, ϑ΄и ϑ˝ собственные углы падения, отражения и преломления световой волны.
 . .
|
|
 (х,t) любой точки среды с координатой х в любой момент времени t называется уравнением волны.
(х,t) любой точки среды с координатой х в любой момент времени t называется уравнением волны.
 (х,t) – смещение точек через время t, за которое волна распространяется на расстояние х =
(х,t) – смещение точек через время t, за которое волна распространяется на расстояние х =  t (
t (  - скорость распространения волны).
- скорость распространения волны).
 , которая называется волновым числом.
, которая называется волновым числом.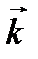 показывает направление распространения волны в данной точке волнового фронта (рис.28.1).
Перепишем выражение (28-1) в виде
показывает направление распространения волны в данной точке волнового фронта (рис.28.1).
Перепишем выражение (28-1) в виде
 .
Преобразуем отношение
.
Преобразуем отношение 
 .
Тогда уравнение волны запишется в виде
.
(28-2)
.
Тогда уравнение волны запишется в виде
.
(28-2)



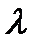

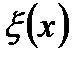
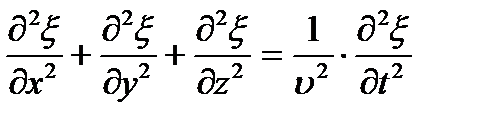
 (см. часть 2, лекция №20), в данном случае (ЭМИ) сторонние силы не связаны ни с химическими, ни с тепловыми процессами, они также не могут быть магнитными силами, по тому, что такие силы работу над зарядами не совершают. Остается заключить, что индукционный ток обусловлен возникающим в проводе электрическим полем, тогда ЭДС
(см. часть 2, лекция №20), в данном случае (ЭМИ) сторонние силы не связаны ни с химическими, ни с тепловыми процессами, они также не могут быть магнитными силами, по тому, что такие силы работу над зарядами не совершают. Остается заключить, что индукционный ток обусловлен возникающим в проводе электрическим полем, тогда ЭДС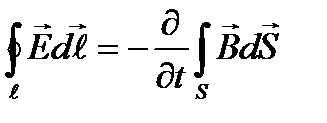
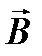 может быть
может быть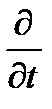 )
)
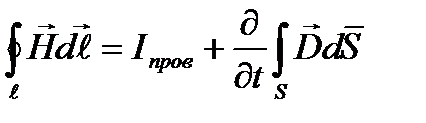
 ), но и перемещенным электрическим полем («ток смещения»
), но и перемещенным электрическим полем («ток смещения»  ).
).
 ℰℰ
ℰℰ 

 и
и  (лекция №18, часть 3)
(лекция №18, часть 3)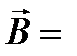 μμ
μμ 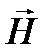
 и
и  (лекция №23, часть 3)
(лекция №23, часть 3) σ
σ 


 - некоторый вектор в нашем случае:
- некоторый вектор в нашем случае:  (О функции rot
(О функции rot 




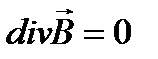

 ,
,


 ,
,

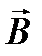 ,
,  .
.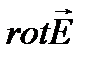 . Вектор ротора приложен в центре поля перпендикулярно плоскости его силовых линий (в случае круговых линий – в центре окружностей) и направлен относительно них согласно правилу правого винта.
. Вектор ротора приложен в центре поля перпендикулярно плоскости его силовых линий (в случае круговых линий – в центре окружностей) и направлен относительно них согласно правилу правого винта. .
.
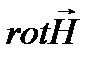 )
)
 Подставим ℰ
Подставим ℰ  μ
μ  в выражение для скорости u. Если среда – вакуум, то ℰ = 1, μ = 1, тогда получим u = ,
в выражение для скорости u. Если среда – вакуум, то ℰ = 1, μ = 1, тогда получим u = ,
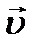


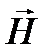
 и
и  +
+  по известному положению в момент
по известному положению в момент 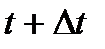
 . (Напомним, что вектор
. (Напомним, что вектор  . равный по модулю волновому числу
. равный по модулю волновому числу 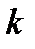 = 2πۤ/λ и имеющий направление по нормали к волновой поверхности)
= 2πۤ/λ и имеющий направление по нормали к волновой поверхности)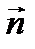



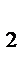

 ℰ
ℰ