|
|
Топологические свойства однослойных, двухслойных и трехслойных НС. Теорема Минского
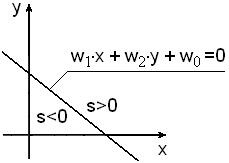
Количество слоев НС определяет ее возможности по распознаванию изображений. Если рассматривать в качестве входного вектора НС координаты некоторой точки плоскости, то каждый нейрон однослойной сети может определить факт принадлежности точки определенной полуплоскости. Будем считать, что (x,y) – координаты точки плоскости и одновременно входные сигналы нейрона. Соответствующая схема нейрона представлена на рис.14.1.
Рис.14.1. Нейрон и соответствующая разделительная линия двух полуплоскостей
Сигмоидальная сумма определяется по следующей формуле:
Соответствующее каноническое уравнение прямой, являющейся границей двух полуплоскостей, имеет вид:
В одной полуплоскости сигмоидальная сумма s>0, а в другой s<0, что отображено на рис.14.1. Известно несколько теорем об ограниченности функциональных возможностей НС. Одной из таких теорем является теорема Минского. Теорема Минского 1: Однослойный персептрон не может воспроизвести функцию «исключающее или». Рассмотрим доказательство теоремы, построенное на геометрической интерпретации входных сигналов персептрона и логической функции. Персептрон должен иметь два входа, что соответствует двум аргументам функции «исключающее ИЛИ». Таблица истинности этой функции показана на рис.14.2.
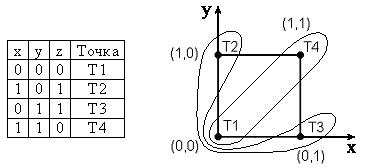
Рис.14.2. Множества, которые соответствуют функции “исключающее ИЛИ”
Будем считать, что x, y – координаты точек плоскости, имена которых указаны в правом столбике таблицы истинности. Точки Т1 и Т4 должны принадлежать множеству, которое соответствует значениям функции z=1, а точки Т2 и Т3 – множеству z=0. Один из вариантов конфигурации таких множеств приведен на рис14.2. На вход персептрона подаются координаты (х,у), которые умножаются на весовые коэффициенты w1 и w2, а затем складываются со смещением w0:
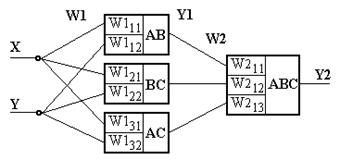
Полученная синаптическая сумма преобразуется активационной функцией в выходной сигнал Двухслойная НС может решить более сложные задачи, комбинируя во втором слое нейронов выходные сигналы нейронов первого слоя. Для задачи идентификации положения точки этот тезис можно интерпретировать следующим образом: выходной сигнал нейрона второго слоя определяет факт принадлежности точки выпуклого многоугольника, граничные линейные участки которого определяются нейронами первого слоя. Например, для разделения множеств W1 и W2, показанных на рис.14.3, необходима двухслойная НС, первый слой которой должен состоять из трех нейронов, а второй - из одного.
Рис.14.3. Области классификации точек плоскости и соответствующая двухслойная нейронная сеть, идентифицирующая точки плоскости
Весовые коэффициенты первого слоя рассчитываются на основе геометрических представлений и следующих аналитических соотношений:
Из приведенных соотношений видно, что матрица весовых коэффициентов W1 и вектор смещений V1 могут быть получены в результате трансформации системы уравнений для прямых, проходящих через заданные точки плоскости. Важным моментом является переход от системы уравнений к системе неравенств, который осуществляется для каждого равенства так, чтобы точки, принадлежащие выпуклому многоугольнику, обеспечивали компонентам функции Q(X,Y) одинаковые знаки, для определенности - положительные. Из аналитической геометрии известно, что если прямая задается уравнением: aX+bY+c=0, то вектор (a,b) направлен в сторону положительной полуплоскости, образуемой этой прямой. Таким образом, если вектор (a,b) направлен во внешнюю сторону многоугольника, то для получения требуемого неравенства необходимо изменить знаки коэффициентов: -aX-bY-c>0, в противном случае изменения знаков не требуется: aX+bY+c>0. Для примера, приведенного на рис.14.3, весовые коэффициенты нейронов первого слоя определяются следующим образом:
Результирующий сигнал
Рис. 14.4. Ступенчатая активационная функция
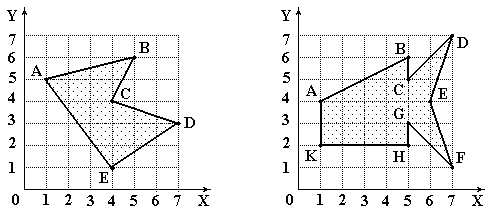
Трехслойные НС позволяют распознавать области плоскости, форма которых не ограничена требованием выпуклости, так как она образуется логической комбинацией выпуклых многоугольников. На рис.14.5 представлены примеры таких фигур.
Рис.14.5. Распознаваемые области
Точки A, B и D лежат на одной прямой и это позволяет ограничить число нейронов в первом слое до пяти. Если бы продолжение прямой CD проходило выше точки А, то НС пришлось бы дополнить шестым нейроном.
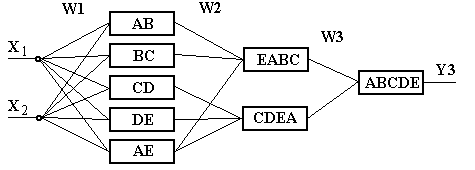
Рис.14.6. Пример трехслойной нейронной сети
Первый слой НС определяет множество полуплоскостей, второй слой нейронов формирует выпуклые многоугольники, а третий слой комбинирует многоугольники для образования требуемых фигур, не обладающих свойством выпуклости.
Свойства НС Хопфилда
НС Хопфилда является однослойной НС, предназначенной для распознавания бинарных образов [2,18]. Сеть охвачена обратной связью (feedback loop), как показано на рис.15.1. Каждая линия обратной связи содержит элемент задержки на 1 такт времени
Рис.15.1. НС Хопфилда
Сеть используется в качестве ассоциативной памяти. Сеть должна уметь на основе двоичного неидеального сигнала на входе сформировать сигнал идентификации или отказа на выходе. Весовые коэффициенты сети вычисляются на основе эталонной информации, которая имеет формат входной информации.
Число запоминаемых образов должно удовлетворять ограничению:
Возможными результатами переходного процесса могут являться: o Одно из эталонных изображений o Негатив одного из эталонных изображений o Зацикливания длины 2 некоторых битов выходного сигнала – отказ от распознавания. Рассмотрим пример распознавания бинарных изображений с помощью НС Хопфилда. Даны два образца изображений:
и входное, распознаваемое изображение
В этом случае m=2, n=16, т.е. выполняется неравенство Данные матрицы преобразуем по столбцам в вектора:
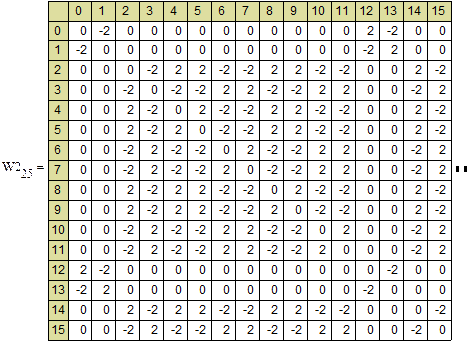
Матрица весовых коэффициентов сети:
Формирование i-го элемента выходного сигнала происходит следующим образом: i-я строка матрицы скалярно умножается на вектор входного сигнала. Полученное значение подставляется в активационную функцию. Например, первый элемент выходного вектора равен:
Выходной вектор НС имеет вид:
Второй и третий выходные сигналы рассчитываются аналогично, но в качестве входного сигнала используется предыдущий выходной сигнал.
Третий выходной сигнал в точности повторяет первый, это говорит о зацикливании нейронной сети.
Рис. 15.2. Два образцовых изображения Z1, Z2, входной вектор Z3, выходные вектора Y1, Y2, Y3.
Приведенный пример расчета показывает, что переходной процесс формирования выходного сигнала был коротким, что свойственно для НС Хопфилда.
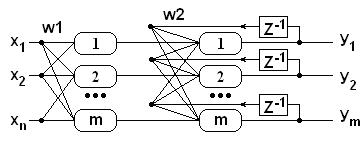
Свойства НС Хемминга НС Хэмминга формирует на выходе номер распознанного эталона [2,18]. Сеть состоит из двух слоев, с обратной связью во втором слое, как показано на рис.16.1. Сеть выбирает только один эталон с минимальным расстоянием Хэмминга до входного сигнала и активизирует только один выход сети, соответствующий этому эталону. Первый слой НС формирует на своем выходе вектор, состоящий из коэффициентов корреляции входного образа со множеством запомненных образов. Второй слой определяет наибольший коэффициент корреляции и устанавливает в «1» соответствующую выходную линию. Второй слой реализует стратегию WTA (winner take all) – «победитель получает все». Входной и выходной слои содержит столько пар нейронов, сколько образов должна запомнить НС Хэмминга.
Рис.16.1. НС Хэмминга
Весовые коэффициенты 1-го слоя инициируются следующими значениями: Выходные сигналы первого и второго слоев имеют вид:
Активационная функция первого слоя – линейная функция, второго слоя – положительная линейная ограниченная функция. Активационная функция и матрица второго слоя НС Хэмминга показаны на рис.16.2.
Рис.16.2. Активационная функция и матрица весовых коэффициентов второго слоя
Матрица
|
|

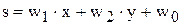 .
. .
.
 .
.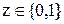 . Выше было показано, что персептрон осуществляет линейное разделение точек плоскости, однако, как видно из рисунка, пары точек {Т1,Т4} и {Т2,Т3} невозможно разделить прямой. Таким образом, персептрон не способен воспроизвести функцию «исключающее или».
. Выше было показано, что персептрон осуществляет линейное разделение точек плоскости, однако, как видно из рисунка, пары точек {Т1,Т4} и {Т2,Т3} невозможно разделить прямой. Таким образом, персептрон не способен воспроизвести функцию «исключающее или».
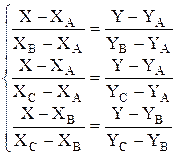 ,
, 
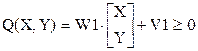 .
.
 ,
,  ,
,  ,
,  .
. преобразуется с помощью активационной функции, приведенной на рис. 14.4. Если классифицируемая точка попадает в положительную полуплоскость, то выходной сигнал
преобразуется с помощью активационной функции, приведенной на рис. 14.4. Если классифицируемая точка попадает в положительную полуплоскость, то выходной сигнал  . Точку можно считать принадлежащей заданной области, только в том случае, если все выходные сигналы равны 1. Весовые коэффициенты нейрона второго слоя должны быть подобраны так, чтобы выполнялось неравенство:
. Точку можно считать принадлежащей заданной области, только в том случае, если все выходные сигналы равны 1. Весовые коэффициенты нейрона второго слоя должны быть подобраны так, чтобы выполнялось неравенство:  . Например,
. Например, 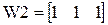 ,
,  .
.
 (unit delay element). Обратная связь элементов типа «связь самого с собой» в сети не используется.
(unit delay element). Обратная связь элементов типа «связь самого с собой» в сети не используется.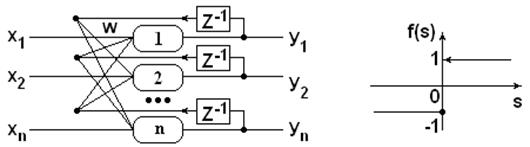
 - где
- где 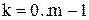 ,
, 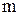 - количество эталонов. Если
- количество эталонов. Если  , то сигнал распознан.
, то сигнал распознан.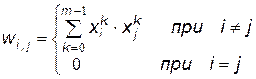 . (15.1)
. (15.1) . Кроме того, эталоны попарно должны иметь существенные корреляционные отличия. Появление на входе системы нового сигнала вызывает переходный процесс, который описывается следующими векторными соотношениями:
. Кроме того, эталоны попарно должны иметь существенные корреляционные отличия. Появление на входе системы нового сигнала вызывает переходный процесс, который описывается следующими векторными соотношениями: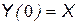 ,
,  ,
, 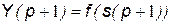 .
. .
. .
. ,
, 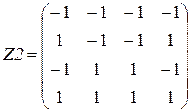
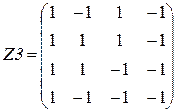 .
.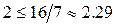 , возможно использование НС Хопфилда.
, возможно использование НС Хопфилда. ,
,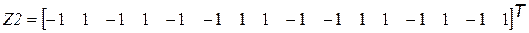 ,
, .
.



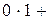




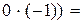
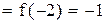 .
. .
.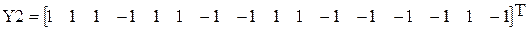 ,
, .
.
 ,
, 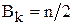 , где
, где  - номер эталона,
- номер эталона,  - номер входного сигнала. Весовые коэффициенты второго слоя назначаются следующим образом:
- номер входного сигнала. Весовые коэффициенты второго слоя назначаются следующим образом: 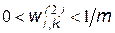 , если
, если  , иначе
, иначе 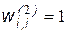 . Число запоминаемых образов должно удовлетворять ограничению:
. Число запоминаемых образов должно удовлетворять ограничению:  .
.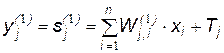 ,
, 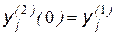 ,
,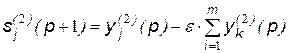 ,
, 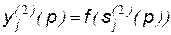 .
.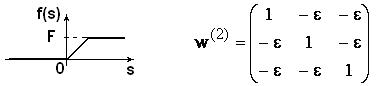
 имеет отрицательные и положительные элементы. Такая матрица сохраняет наибольший сигнал и ослабляет до нуля меньшие сигналы. От каждого сигнала, кроме максимального, вычитается
имеет отрицательные и положительные элементы. Такая матрица сохраняет наибольший сигнал и ослабляет до нуля меньшие сигналы. От каждого сигнала, кроме максимального, вычитается 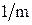 часть других, пока он не станет нулевым (отрицательные значения исключены активационной функцией).
часть других, пока он не станет нулевым (отрицательные значения исключены активационной функцией).