|
|
Метод обратного распространения ошибки
Обучение нейронной сети методом градиентного поиска, с учетом слоистой структуры, называется методом обратного распространения ошибки (МОРО – back propagation algorithm)). Данный метод хорошо изучен и достаточно устойчив [2,14,18]. Сигналы ошибки распространяются от выходов НС к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Согласно методу наименьших квадратов минимизируемой целевой функцией ошибки НС является сигнал ошибки обучения:
где
где
где
Здесь суммирование по Введя новую переменную
получим рекурсивную формулу для расчетов величин
Для выходного слоя:
Теперь можно записать основное выражение для весовых коэффициентов в обобщенном виде:
Рассмотренный метод обучения не всегда приводит к правильному решению, что обусловлено рядом причин. Во-первых, в процессе обучения может возникнуть ситуация, когда большие положительные или отрицательные значения весовых коэффициентов сместят рабочую точку на сигмоидах многих нейронов в область насыщения. Малые величины производной от активационной функции приведут к остановке обучения, что парализует НС. Во-вторых, применение метода градиентного спуска не гарантирует, что будет найден глобальный, а не локальный минимум целевой функции. Эта проблема связана еще с одной, а именно - с выбором величины скорости обучения. Занижение скорости обучения приводит к увеличению длительности обучения. С другой стороны, слишком большие коррекции весов могут привести к потере устойчивости процесса обучения. Несмотря на указанные недостатки, рассмотренный метод считается одним из наиболее эффективных методов обучения нейронных сетей.
Матричная форма МОРО
Наиболее просто метод обратного распространения ошибки представляется в матричной форме. Прямое распространение сигнала по НС, состоящей из N слоев, описывается следующей системой уравнений:
Вектор входного сигнала наращивается единичной компонентой, так как необходимо учитывать величину смещения в каждом слое нейронов. Обратное распространение сигнала ошибки по НС позволяет вычислить корректирующие коэффициенты с помощью следующих уравнений:
Коррекция весовых коэффициентов НС проводится с помощью следующих уравнений:
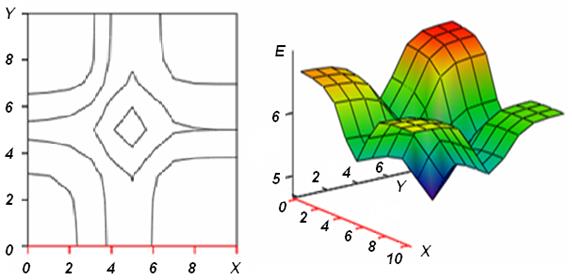
где Приведенные выше уравнения являются компактной формой описания метода обратного распространения ошибки, используемого для обучения нейронных сетей. Применение данных уравнений позволяет строить модели НС с произвольным числом слоев. Пример зависимости невязки от величины весовых коэффициентов приведен на рис.19.1. Алгоритм построения графиков: трехслойная НС была обучена распознаванию заданных образов, произвольным образом во втором и третьем слоях выбраны два весовых коэффициента, в квадратной окрестности, окружающей оптимальные значения коэффициентов, задана сеть значений коэффициентов, для которых вычислена невязка.
Рис.19.1. Графики зависимости невязки на выходе НС от значений двух весовых коэффициентов
Приведенные графики наглядно показывают наличие минимума невязки и демонстрируют сложность исследуемой поверхности: к точке минимума сходится 4 взаимно ортогональных канала.
|
|
 , (18.1)
, (18.1) - реальное выходное состояние нейрона j выходного слоя N нейронной сети при подаче на ее входы p-го образа;
- реальное выходное состояние нейрона j выходного слоя N нейронной сети при подаче на ее входы p-го образа;  - идеальное (желаемое) выходное состояние этого нейрона. Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью образам. Минимизация ведется методом градиентного спуска, что означает подстройку весовых коэффициентов следующим образом:
- идеальное (желаемое) выходное состояние этого нейрона. Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью образам. Минимизация ведется методом градиентного спуска, что означает подстройку весовых коэффициентов следующим образом: ,
, - весовой коэффициент синаптической связи;
- весовой коэффициент синаптической связи;  - номер нейрона;
- номер нейрона;  - номер входа нейрона;
- номер входа нейрона;  - номер слоя;
- номер слоя;  - коэффициент скорости обучения,
- коэффициент скорости обучения,  . Производная сложной функции имеет вид:
. Производная сложной функции имеет вид: ,
, - выход нейрона
- выход нейрона  - взвешенная сумма входных сигналов, то есть аргумент активационной функции. Для производной сигнала ошибки по выходному сигналу имеем:
- взвешенная сумма входных сигналов, то есть аргумент активационной функции. Для производной сигнала ошибки по выходному сигналу имеем: .
. выполняется среди нейронов слоя
выполняется среди нейронов слоя  .
. ,
, слоя
слоя  слоя
слоя  :
: .
. .
.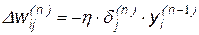
 ,
,  , …,
, …, ,
,  , …,
, …, ,
,  .
. , …,
, …, ,…,
,…,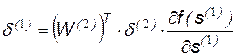 .
. ,…,
,…,  ,
, ,…,
,…,  ,
, ,
,  .
. – коэффициент скорости обучения.
– коэффициент скорости обучения.