|
|
Расчет переходных процессов классическим методомОбщие сведения В курсовой работе «Дополнительные разделы теории цепей» следует произвести расчет переходных процессов в линейных электрических цепях изученными методами. В работе приводится 100 вариантов задания. Вариант определяется двумя последними цифрами номера зачетной книжки студента. Если последняя и предпоследняя цифры нули, то нужно выполнять 100-й вариант. Результаты выполнения курсовой работы оформляют в виде пояснительной записки, имеющей титульный лист, где указывают следующее: Министерство образования и науки Российской Федерации, Сибирский федеральный университет, кафедра «Радиотехники», фамилия, инициалы студента, номер зачетной книжки. В нижней части титульного листа указывают год, месяц и число окончания выполнения курсовой работы. Титульный лист оформляют на бумаге форматом 297х210. Материал в пояснительной записке рекомендуется излагать в том порядке, в каком выполняется курсовая работа. В тексте записки формулы приводятся в общем виде и лишь затем в них подставляют числовые значения. Рядом с формулами делаются ссылки на соответствующие литературные источники. Весь графический материал, приводимый в записке (схемы, графики и т.д.), рекомендуется выполнять на миллиметровой бумаге того же формата, что и листы пояснительной записки. Графический материал располагают в тех местах записки, к которым он относится. К иллюстрациям делают надписи с тематическим названием. В конце пояснительной записки приводят список использованной литературы.
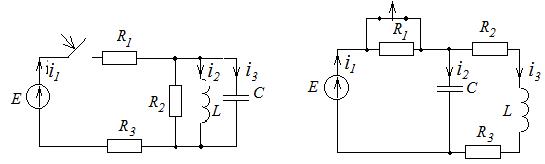
Задание на курсовую работу Задача. Дана электрическая цепь, в которой происходит коммутация (схемы цепей на рис. 1-20). В цепи действует источник ЭДС. Параметры цепи даны в таблице 1. Требуется: 1. Определить зависимость тока от времени после коммутации в одной из ветвей цепи или напряжения на каком-либо элементе или между заданными точками схемы. Задачу следует решить двумя методами: классическим и операторным, если действует постоянная ЭДС. 2. Заменив постоянную ЭДС в схеме гармонической, частота, амплитуда и начальная фаза которой для каждого варианта даны в таблице 2, решить задачу любым методом. 3. На основании полученных аналитических выражений построить графики искомой величины в функции времени в интервале от t=0 до 4. Для данной цепи определить комплексную передаточную характеристику (комплексную передаточную проводимость или комплексный коэффициент передачи по напряжению); рассчитать и построить графики амплитудно-частотной и фазочастотной характеристик. 5. Используя операторный метод, определить временные характеристики цепи: переходную h(t)и импульсную g(t) и построить их графики. 6. Используя интегралы Дюамеля, рассчитать и построить отклик цепи на импульсный сигнал, поданный на вход вместо постоянной ЭДС. В таблице 3, в соответствии с номером варианта, указан номер рисунка, на котором приведена форма импульсного сигнала (рис.21-28), а также его амплитуда. Примечание: 1. Длительность импульса принять равной 2.Сигналы на рис.27-28 содержат показательную функцию
Рис. 1 Рис. 2
Рис. 3 Рис. 4
Рис. 5 Рис. 6
Рис. 7 Рис. 8
Рис. 9 Рис. 10
Рис. 11 Рис. 12
Рис. 13 Рис. 14
Рис. 15 Рис. 16
Рис. 17 Рис. 18
Рис. 19 Рис. 20
Рис. 21 Рис. 22
Рис. 23 Рис. 24
Рис. 25 Рис. 26
Рис. 27 Рис. 28
2.Указания к решению задачи
Расчет переходных процессов классическим методом Классическим называют метод расчета, в котором решение системы уравнений, описывающих переходные процессы в разветвленной цепи, находят в виде суммы принужденного и свободного решений (составляющих). Определение постоянных интегрирования, входящих в выражения для свободных составляющих, производят путем совместного решения системы алгебраических уравнений по известным значениям корней характеристического уравнения, а также по известным значениям свободных составляющих токов (или напряжений) и их производных по времени, взятых при t = 0, т. е. i(t) = iПР(t) + iCB(t), U(t) = UПР(t) + UCВ(t). Поскольку принужденная составляющая определяется воздействующей ЭДС, то для её нахождения можно использовать все известные методы расчета цепи в установившемся режиме, метод уравнений Кирхгофа, метод контурных токов, метод узловых потенциалов, метод эквивалентного генератора и др. Свободные составляющие токов и напряжений представляют собой общее решение системы однородных линейных дифференциальных уравнений, составленных для цепи после коммутации. Свободные составляющие токов (напряжений) в цепи могут быть представлены в виде суммы экспоненциальных слагаемых, число членов которой равно числу корней характеристического уравнения. Для заданной цепи степень характеристического уравнения не зависит от выбора контуров, для которых составляются уравнения по второму закону Кирхгофа. Степень характеристического уравнения равна числу независимых начальных условий в послекоммутационной цепи после максимального её упрощения (параллельно соединенные ёмкости заменяются одной ёмкостью, последовательно включенные индуктивности также заменяются одной индуктивностью и т. д.). Система уравнений составляется обычным образом: Для свободных составляющих токов в ветвях в уравнениях, составленных по второму закону Кирхгофа, следует освободиться от принуждающих ЭДС, т. е. взять правые части равные нулю. Поскольку решение для свободных составляющих ищется в виде
Заменив в исходной системе дифференциальных уравнений
получим систему однородных алгебраических уравнений относительно свободных составляющих токов в ветвях. Решив эту систему, получим для тока в k-ой ветви
где Δ – определитель системы, Δk – определитель, полученный заменой k-го столбца в определителе системы на столбец из правых частей уравнений равных нулю, т. е. Δk = 0. А это значит, что система уравнений имеет решение, отличное от нулевого решения, если определитель Δ = 0. Уравнение Δ(p) = 0 называют характеристическим уравнением системы. Единственным неизвестным в нём является р. Корни характеристического уравнения могут быть действительными и комплексными. Если корни комплексные, то они образуют комплексно-сопряженные пары. Действительные части всех корней отрицательны, что физически обусловлено затуханием свободных составляющих в пассивных цепях с течением времени. Пусть характеристическое уравнение имеет n корней, тогда
где Ak – постоянная интегрирования. Число слагаемых в последнем выражении определяется степенью характеристического уравнения: а) уравнение первой степени имеет только один действительный и отрицательный корень (цепи первого порядка RL и RC); б) уравнение второй степени может иметь два действительных отрицательных неравных корня (апериодический режим в RLC-цепи), два действительных равных отрицательных корня (критический режим) либо два комплексно-сопряженных корня с отрицательной действительной частью (колебательный режим в RLC-цепи). В последнем случае свободная составляющая имеет вид
где В общем случае сложная цепь может иметь все три вида корней характеристического уравнения и решение для свободных составляющих представляет собой совокупность экспонент и затухающих по экспоненте синусоид. Постоянные интегрирования находятся из системы уравнений, полученной (n–1) – кратным дифференцированием выражения для свободной составляющей с учетом уравнений Кирхгофа для послекоммутационной цепи при t = 0 и независимых начальных условий, т. е. из решения системы уравнений
Определив Аk, можем записать полное выражение для искомой величины i(t) = iПР(t) + iCB(t), U(t) = UПР(t) + UCB(t). Таким образом, расчет переходных процессов классическим методом производится в следующем порядке: 1. Производится расчет режима до коммутации, где находятся значения токов в индуктивностях и напряжений на ёмкостях в момент времени 2. Производится расчет принужденного режима после коммутации. 3. Составляется система уравнений Кирхгофа для цепи после коммутации. 4. Находится общее решение системы однородных уравнений (определяется характеристическое уравнение и находятся его корни). Определяются зависимые начальные условия из независимых начальных условий и системы уравнений Кирхгофа для t = 0. 5. Определяются постоянные интегрирования по начальным условиям. 6. Записывается полное решение в виде i(t) = iПР(t) + iCB(t), U(t) = UПР(t) + UCB(t). Пример 1. В цепи (рис. 29) действует постоянная ЭДС Е = 100В.
Рис. 29
R1 = 10Ом, R2 = 20Ом, R3 = 50Ом, R4 = 20Ом, L = 1мГН, C = 100мкФ. Требуется определить закономерность изменения во времени тока iL = i3. Решение. 1. Независимыми начальными условиями будут ток iL(0–) = i3(0–) и напряжение на ёмкости UC(0–), определим их:
2.Составим систему уравнений по законам Кирхгофа для послекоммутационной схемы:
Для свободных составляющих токов эта система имеет вид:
Произведя алгебраизацию системы, получим:
Данная система имеет решение, отличное от нулевого решения, если определитель системы равен нулю, т. е.
Раскрывая определитель, получим характеристическое уравнение второй степени:
3. Общее решение для тока iLCB(t) имеет вид
4. Найдём принужденную составляющую тока:
5. На основании законов коммутации iL(0–) = iL(0) и UC(0–) = UC(0). Определим производную
отсюда
6. Определим постоянные интегрирования A1 и A2:
отсюда A1 = 0,805; A2= – 1,055. 7. Запишем выражение для искомого тока в виде
i3(t) = i3ПР(t) + i3CB(t) = 1,25 + 0,805e–680t – 1,055e–19480t. Графики принужденной, свободных оставляющих и полного тока приведены на рис. 30.
Рис. 30
Пример 2. Решить задачу, приведенную в примере 1, заменив постоянную ЭДС гармонической e(t) = 100cos(ωt+ 60°), где ω= 10000P/C. Решение. 1.Определим независимые начальные условия UC(0–) и iL(0). На основании закона Ома для до коммутационной цепи имеем
Подставив значения R, L, C, E, получим
Мгновенные значения напряжения и тока
UC(t) = 1,64cos(ωt + 150°), iL(t) = 0,04cos(ωt + 137°),
для t = 0 UC(0–) = 1,64cos150° = –1,42В, iL(0–) = 0,04cos137° = 0,03A.
Система уравнений Кирхгофа для цепи после коммутации не зависит от вида ЭДС, следовательно, можно использовать систему из примера 1. Характеристическое уравнение системы и общее решение для тока имеет такой же вид, как и в первом примере. Найдем принужденную составляющую тока i3ПР. Как и в цепи до коммутации
Подставив значения R, L, C, E, получим
для t = 0 iLПР(0) = 0,04cos(–53°) = 0, 046А.
Зависимое начальное условие
Определим постоянные интегрирования А1 и А2:
для t = 0
отсюда А1 = –0,1548, А2 = 0,0788. Полное выражение для искомого тока:
i3(t) = 0,076cos(ωt – 53°) – 0,546e–680t + 0,0788e–19480t.
Графики принужденной и свободных составляющих тока приведены на рис. 31.
Рис. 31
Следует отметить, что довольно часто при нахождении постоянных интегрирования можно в системе уравнений использовать не производную искомой величины по времени, а интеграл. Например, при нахождении тока через ёмкость имеем iC(0) = iCПР(0) + А1 + А2. Поскольку в систему уравнений, составленных по законам Кирхгофа, производная di/dt не входит, используем интеграл от тока по времени. Действительно,
для t = 0
Таким образом, система уравнений для расчета постоянных интегрирования
Аналогичное решение можно предложить, если в задаче необходимо найти напряжение на индуктивности:
|
|
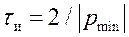 |.Здесь |
|.Здесь | |-меньший по модулю корень характеристического уравнения. На графиках показать каждую экспоненту свободной составляющей, их сумму, а также принужденную составляющую после коммутации. Слева от оси ординат изобразить часть до коммутационной составляющей искомой величины (для постоянной и гармонической ЭДС отдельно).
|-меньший по модулю корень характеристического уравнения. На графиках показать каждую экспоненту свободной составляющей, их сумму, а также принужденную составляющую после коммутации. Слева от оси ординат изобразить часть до коммутационной составляющей искомой величины (для постоянной и гармонической ЭДС отдельно). .
. , где
, где  .
.












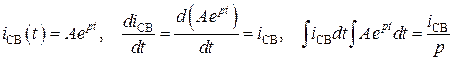 .
. ,
, ,
, ,
,
 .
.

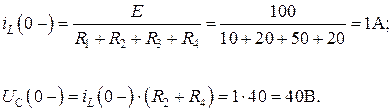 ;
;




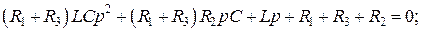


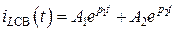 .
. .
. в момент времени t = 0 (зависимое начальное условие). Из второго уравнения системы для t = 0 следует
в момент времени t = 0 (зависимое начальное условие). Из второго уравнения системы для t = 0 следует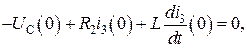
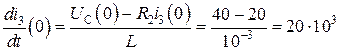 В/Гн.
В/Гн.







 .
.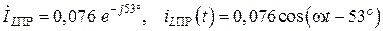 ,
, в момент t = 0 определим из второго уравнения системы
в момент t = 0 определим из второго уравнения системы В/Гн.
В/Гн. ,
,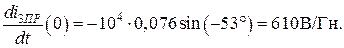

 ,
,


 ,
, .
.
