|
|
Оценка стоимости ценных бумаг с фиксированным доходомК ценным бумагам с фиксированным доходом принято относить облигации и привилегированные акции. Определение, классификация, экономическое содержание и юридическая природа этих инструментов являются предметом рассмотрения других курсов; здесь же рассмотрим лишь их оценку при известной альтернативной доходности r.
Оценка бескупонных (дисконтных) облигаций По определению, бескупонные (дисконтные) облигации, или, как их еще называют, облигации с нулевым купоном, реализуются со скидкой (дисконтом) от номинала (номинальной или нарицательной стоимости) и погашаются по номиналу. Никаких промежуточных выплат эти облигации не предусматривают. Если обозначить через PV– текущую стоимость облигации; F– ее номинальную стоимость; а n–число лет до погашения, то оценка будет производиться по формуле:
В формуле (2.14) число лет до погашения может быть как целым, так и дробным.
Пример. Необходимо оценить шестимесячную государственную облигацию номиналом в 1000 руб., если альтернативная годовая доходность составляет 16%. Решение. Применяя формулу (2.14) с учетом времени до погашения, равного половине года, получаем PV = 1000/(1 + 0.16)1/2 = 928.50 руб.
Оценка купонных облигаций6 В отличие от бескупонных, купонные облигации предполагают регулярную выплату процентного дохода, обычно по фиксированной ставке в процентах от номинальной стоимости, а в конце срока обращения вместе с последним процентным платежом погашается номинальная стоимость облигации. Купонную ставку принято обозначать rc, ее значение равно суммарному годовому процентному доходу, поделенному на номинал облигации. Если частота купонных выплат по облигации выше, чем один раз в год, то купонные платежи с рассчитываются как годовой процентный доход по облигации, деленный на количество выплат в году.
Пример. Облигация имеет номинальную стоимость $1000 и купонную ставку 12%. Если проценты начисляются 1 раз в год, то выплаты составят $120 в конце каждого года вплоть до срока погашения. Если выплаты предусмотрены два раза в год, то платить будут по $60 в конце каждого полугодия. При поквартальной выплате процентов доход кредитора составит $30 в конце каждого квартала.
Если через m обозначить число периодов, оставшихся до погашения облигации, то в приведенных выше обозначениях формула (2.13) для купонной облигации примет вид
Соотношение (2.15) достаточно легко упростить, используя формулу (2.7) для дисконтированной стоимости срочного аннуитета с постоянными платежами:
Из приведенной формулы следует, что текущая стоимость облигации в значительной степени зависит от нормы доходности, которую требует рынок от ценных бумаг данного уровня риска. Если эта рыночная норма доходности (необходимый уровень дохода) превышает установленную купонную ставку, облигация продается со скидкой (дисконтом) от номинала. В противоположном случае облигация продается с премией. При совпадении требуемого уровня дохода и купонной ставки облигация продается по номиналу. Можно также показать, что при заданном изменении необходимого уровня доходности цена облигации изменится тем сильнее, чем дольше период времени до ее погашения.
Пример. Рассчитать рыночную стоимость облигации номиналом 1000 руб. с поквартальной выплатой купонного дохода. До погашения облигации осталось два года. Купонная ставка - 10%; в качестве ставки доходности по альтернативным инвестициям принять 8% годовых. Решение. Так как доход по облигации выплачивается четыре раза год, то величина купонного платежа составит с = 0.1•1000/4 = 25 руб. Квартальная ставка rкв может быть найдена из соотношения (1+ rкв)4 = 1+ 0.08, откуда rкв = 0.0194 или 1.94% (при этом предполагается, что альтернативная ставка начисляется один раз в год). Тогда в соответствии с формулой (2.16): PV = 25[1-(1+0.0194)-8]/0.0194 + 1000/(1+0.0194)8. = 1041 руб. 13 коп. Следует отметить, что оценочная стоимость облигации выше номинала: это объясняется тем, что купонная ставка превышает альтернативную доходность. Оценка бессрочных облигаций и привилегированных акций Хотя правовая природа акций и облигаций принципиально различная, с финансовой точки зрения процедура их оценки может быть сходной, если и тот, и другой инструменты предполагают фиксированные регулярные выплаты дохода держателям. Для оценки бессрочного финансового инструмента следует использовать формулу текущей стоимости бессрочного аннуитета (2.11):
где с – доход за соответствующий период, r – периодическая ставка ожидаемой доходности. Пример. Рассчитать рыночную стоимость привилегированной акции номиналом 10 руб., ставкой дивиденда – 15% и выплатой дохода два раза в год. Ставка рыночной капитализации - 20% годовых. Решение. Так как дивиденд по акции выплачивается два раза год, то его величина составит 0.15*10/2 = 0.75 руб., или 75 коп. Дивиденд выплачивается в конце каждого полугодия, следовательно необходимо определить полугодовую ставку дисконтирования rпг на основе заданной ставки рыночной капитализации: (1+ rпг)2 = 1+ 0.20, откуда rпг =0.0954. Из формулы (2.11) PV = 0.75/0.0954 = 7 руб. 86 коп. Оценка обыкновенных акций Оценка рыночной стоимости обыкновенных акций в рамках используемой базовой модели (применительно к акциям она носит название модели дисконтирования дивидендов) существенно осложняется тем обстоятельством, что дивиденды по этим инструментам выплачиваются по результатам хозяйственной деятельности предприятия. Как следствие, необходимо иметь достаточно достоверный прогноз ожидаемых дивидендных выплат. Однако, прогнозирование дивидендов, даже если компания придерживается стабильной дивидендной политики, представляет собой достаточно сложную задачу в силу наличия хозяйственных рисков. Тем не менее, существует ряд приемов и моделей7, позволяющих с определенной степенью точности аппроксимировать будущие выплаты, что, соответственно, делает возможным применение формулы (2.13). Обозначая дивиденды за соответствующий период через Divi , из формулы (2.13) получим:
где r – ставка ожидаемой доходности (рыночной капитализации) за соответствующий период. Следует иметь в виду, что под будущими выплатами (дивидендами) понимаются не только собственно дивиденды, но и ликвидационные выплаты, и выкупные платежи при выкупе акций у акционеров. Бесконечное суммирование в формуле (2.17) может также вызвать вопрос о ее применимости в случае ограниченного периода владения акцией. Однако предположение о возможной продаже акции ее нынешним владельцем не ограничивает применимости формулы (2.17): каждый из последующих покупателей акции даст за нее цену, равную текущей (на момент приобретения) стоимости ожидаемых им денежных поступлений. Более серьезные сомнения в применимости формулы (2.17) может вызвать то обстоятельство, что большинство фирм стабильно реинвестирует значительную часть извлекаемой прибыли, а некоторые за всю свою историю не платили никаких дивидендов в принципе, реинвестируя всю генерируемую прибыль в свою финансово-хозяйственную деятельность. Подробное обоснование применимости модели дисконтированных денежных потоков к оценке акций, по которым выплачиваются ограниченные дивиденды, обычно приводится в курсах корпоративных финансов. В настоящем курсе будет достаточным отметить, что стоимость акции может быть представлена не только как сумма дисконтированных будущих дивидендов, но и как сумма дисконтированных свободных денежных потоков фирмы8 или как сумма дисконтированных средних будущих доходов фирмы плюс дисконтированные возможности роста (последний вариант в случае, если компания выбирает стратегию роста). Дивиденды в последнем случае могут быть незначительными либо нулевыми в течение многих лет, однако рано или поздно рост должен замедлиться, и тогда у фирмы появятся денежные средства для выплаты дивидендов. Некоторые выкладки, обосновывающие применение формулы (2.17) к оценке обыкновенных акций найти в Приложении 1 к настоящей главе. Наиболее часто применяется модель, использующая предположение о постоянном темпе прироста дивидендов – модель Гордона. Если обозначить через g темп прироста дивиденда, то дивиденды последующих лет выразятся через дивиденд в конце первого года Div1 формулами:
Тогда соотношение (2.17) примет вид
которое может быть свернуто на основании предельного перехода в формуле дисконтированной стоимости бессрочного аннуитета при i→∞ (формула (2.12)). В результате получим:
Формула (2.19) и представляет собой модель Гордона. Очевидно, что в реальности трудно ожидать от акций точного следования данной модели даже для компаний с устоявшейся дивидендной политикой. Темп прироста дивидендов с течением времени может изменяться, возможны периоды постоянных по величине дивидендов, которые сменяются периодами роста или уменьшения и т.п. С чисто математической точки зрения учет более сложного характера изменения дивидендов проблемы не составляет и соответствующий материал может быть найден в курсах финансовых вычислений. Следует, однако, иметь в виду, что погрешность прогнозирования дивидендных выплат достаточно велика и может свести на нет самые изощренные математические модели. Именно поэтому на практике для целей оценки используются достаточно простые модели, сочетающие периоды нулевого и равномерного роста. Модель Гордона, в отличие от других приведенных формул, имеет ограниченную применимость: темп прироста дивиденда должен быть строго меньше ставки дисконтирования (это следует непосредственно из формулы (2.19)).
Пример. Оценить рыночную стоимость обыкновенной акции, если в течение ближайших пяти лет дивиденд на нее ожидается постоянным и равным 80 коп., после чего прогнозируется начало неограниченно долгого роста в 5% ежегодно. Выплата дивидендов – один раз в год. Ставка рыночной капитализации - 15% годовых. Решение. Так как дивиденды в течение первых пяти лет прогнозируются постоянными, то для расчета их вклада в оценочную стоимость акции следует использовать формулу для дисконтированной стоимости срочного аннуитета с постоянным платежом (2.8). Дальнейшее ежегодное увеличение дивидендов на 5% учитывается в соответствии с формулой (2.19). При этом результат применения модели Гордона следует дисконтировать на пять лет назад, чтобы получить оценку "сегодня". Расчетная стоимость составит: PV = 0.8[1-(1+0.15)-5]/0.15 + 0.8(1+0.05)/[(0.15-0.05)(1+0.15)5] = = 2.68+4.18 = 6.86. Оценочная стоимость акции составит, таким образом, 6 руб. 86 коп. Изложенный выше подход к оценке финансовых активов на основе дисконтированных денежных потоков базируется на ряде очевидных положений: дисконтируются именно будущие, ожидаемые денежные потоки; прошлые поступления значения для оценки не имеют; ставки дисконтирования должны отражать уровень риска, присущий оцениваемому финансовому активу. Очевидно, что использование описанной модели оценки акций, основанной на дисконтировании будущих дивидендов, требует не только наличия достаточно эффективного финансового рынка, но и весьма высокой профессиональной квалификации аналитиков. Мировая практика наработала ряд альтернативных методов оценки обыкновенных акций. Некоторые из них, в частности модель оценки по стоимости чистых активов и подход, основанный на Р/Е-мультипликаторе будут рассмотрены ниже, применительно к характерным для трансформационных экономик низколиквидным финансовым рынкам. |
|
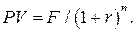 (2.14)
(2.14) (2.15)
(2.15)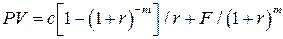 (2.16)
(2.16)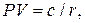 (2.11')
(2.11') (2.17)
(2.17)
 (2.18)
(2.18)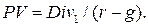 (2.19)
(2.19)