|
|
Доходность финансовых активовСобственно доходность представляет собой относительный показатель, характеризующий отношение дохода на соответствующий актив за определенный период (обычно за год) к рыночной цене актива[27]. Существует несколько подходов к определению показателя доходности. В частности, различают доходность ожидаемую и фактическую (рассчитываемую по фактическим данным). Как следует из предыдущих разделов, основную роль в оценке и анализе играет именно ожидаемая доходность. При расчете доходности для конкретных видов активов может учитываться как собственно доход (дивиденд, процент и др.), так и прирост курсовой стоимости актива. В наиболее общем виде полная доходность за период рассчитывается как отношение дохода на актив плюс прирост его курсовой стоимости за период к рыночной цене на начало периода
Если не учитывать прирост курсовой стоимости актива, то получаем формулу расчета текущей (в случае акций - дивидендной) доходности:
В формулах (2.20) и (2.21) Dt представляет собой доход на актив за год; Pt-1 - цену актива в начале года (в текущий момент), Pt - цену актива в конце года. Показатель текущей доходности для купонной облигации рассчитывается как отношение годового купонного дохода к ее текущей рыночной цене.
Пример. Облигация номинальной стоимостью 1000 руб. имеет ставку купонной доходности 10% годовых с поквартальной выплатой дохода. При курсовой стоимости в 976 руб. показатель текущей доходности облигации составит: 1000*0.10/976 = 0.10246, или 10.246%.
Однако, несмотря на простоту исчисления, текущая доходность не может рассматриваться как вполне корректный показатель доходности финансового инструмента. Наиболее корректным с финансовой точки зрения является показатель полной доходности. Полная доходность наиболее просто определяется для бессрочных облигаций и привилегированных акций, а также бескупонных облигаций: для этого достаточно разрешить соответственно уравнения (2.11') или (2.14) относительно ставки r. Для купонных облигаций основным является показатель доходности к погашению (YTM – от английского Yield to Maturity). Указанный показатель применяемый, как это следует из названия, только к срочным (погашаемым) облигациям, определяется как "процентная ставка, при которой дисконтированная стоимость всех будущих купонных выплаты по облигации, а также ее номинальной стоимости равна ее текущей рыночной цене" [Kohn]. При этом предполагается, что все получаемые купонные платежи могут быть реинвестированы с нормой прибыли, равной этому самому показателю доходности. Как следует из определения, точное значение показателя YTM находится как корень уравнения (2.15) при известной рыночной цене облигации. В соответствии с теоремой Декарта число положительных корней указанного уравнения равно числу перемен знаков в системе коэффициентов этого многочлена. В нашем случае знак меняется один раз. Так как в общем случае уравнение (2.15) представляет собой алгебраическое уравнение высокой степени, решение его без применения финансового калькулятора затруднительно. Поэтому часто применяются приближенные формулы (см., например, [Ковалев],[Kohn], и др). Пример. Рассчитать доходность к погашению облигации номиналом 1000 руб., которая продается за 1041 руб. Купонная ставка составляет 10% годовых, выплата процентов производится два раза в год. До погашения облигации осталось 12 месяцев. Решение. Так как до погашения облигации осталось всего два купонных платежа, полугодовую ставку доходности к погашению YTMполуг можно найти из квадратного уравнения: 1041 = 50/(1+ YTMполуг) + (50+1000)/(1+ YTMполуг)2, которое имеет один положительный корень YTMполуг = 0.0286. Годовая ставка YTM будет определена путем начисления YTMполуг два раза по правилу сложного процента из уравнения (1+ YTMполуг)2 = 1+ YTM, и составит 5.80%. Для сравнения, если бы выплата процентов по облигации производилась один раз в год при прочих равных условиях, доходность к погашению была бы определена из уравнения 1041 = (100+1000)/(1+ YTM), составила бы 5.67%.
Полная доходность обыкновенной акции может в общем виде быть найдена из уравнения (2.17). Для случая постоянного темпа прироста дивиденда полная ожидаемая доходность определится как результат разрешения уравнения (2.19) относительно ставки r.
Другими словами, ставка полной доходности равна дивидендной доходности увеличенной (уменьшенной) на темп роста дивиденда.
|
|
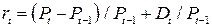 (2.20)
(2.20) (2.21)
(2.21) (2.22)
(2.22)