|
|
Закони Стефана-Больцмана й ВінаВ законі Кірхгофа (6) стверджується, що спектральна густина випромінювальної здатності абсолютно чорного тіла є універсальною функцією, тому знаходження її явної залежності від частоти й температури є важливим завданням теорії теплового випромінювання. Аналізуючи експериментальні дані, вчені И. Стефан і Л. Больцман, застосовуючи лише термодинамічний метод, розв’язали це завдання лише частково, установивши залежність інтегральної випромінювальної здатності абсолютно чорного тіла Re від температури. Цей закон дістав назву закону Стефана-Больцмана,
тобто інтегральна випромінювальна здатність абсолютно чорного тіла пропорційна термодинамічній температурі в четвертому степені. Тут
Закон Стефана-Больцмана, визначаючи залежність Re від температури, не дає відповіді щодо спектрального складу випромінювання абсолютно чорного тіла. Експериментальні криві залежності функції
Рис. 2 Площа, обмежена кривою залежності Німецький фізик В. Він, опираючись на закони термодинаміки й електродинаміки, установив залежність довжини хвилі λ, на яку припадає максимум функції
де b – постійна Віна, її експериментальне значення дорівнює 2,9 · 10-3 мК. Вираз (11) називають законом зміщення Віна, оскільки він показує зсув положення максимуму функції Незважаючи на те, що закони Стефана-Больцмана й Віна відіграють у теорії теплового випромінювання важливу роль, вони не відносяться до фундаментальних законів, тому що не дають загальної картини розподілу енергії випромінювання за частотами при різних температурах. Формула Планка. Виведення законів Стефана-Больцмана й Віна
Значення спектральної випромінювальної здатності абсолютно чорного тіла було знайдено німецьким фізиком М. Планком у 1900 р. Для цього йому довелося відмовитися від одного із основних положень класичної фізики, відповідно до якого енергія будь-якої випромінювальної системи може змінюватися неперервно, тобто приймати довільні значення. Відповідно до висунутої Планком квантової гіпотези, атомні осцилятори випромінюють енергію не безупинно, а певними порціями – квантами, причому енергія кванта пропорційна частоті коливання:
де Оскільки енергія випромінювання випускається порціями, то енергія осцилятора ε може приймати лише певні дискретні значення, кратні цілому числу елементарних порцій енергії ε0:
Використовуючи статистичні методи й квантовий характер теплового випромінювання, М. Планк вивів формулу універсальної функції Кірхгофа
яка блискуче погоджується з експериментальними даними розподілу енергії в спектрах випромінювання абсолютно чорного тіла у всьому інтервалі частот від 0 до ∞ і при різних температурах. Теоретичний зміст цієї формули М. Планк розповів 14 грудня 1900 р. на засіданні Німецького фізичного гуртка. Цей день став датою народження квантової фізики. Використовуючи формулу Планка можна одержати закон Стефана-Больцмана. Згідно з (9)
Введемо позначення х = hv/(kТ), звідки
де Таким чином, дійсно формула Планка дозволяє одержати закон Стефана-Больцмана . Крім того, підстановка числових значень k, с и h дає для постійної Стефана-Больцмана величину, яка добре погоджується з експериментальними даними. Закон зміщення Віна одержимо за допомогою формули (3) і (13):
Досліджуємо вираз (15) на максимум, здійснивши попередньо такі заміни:
Підставимо ці заміни в (15), одержимо
Похідну від (16) прирівняємо до нуля
звідки
Розв’язавши останнє трансцендентне рівняння графічним способом (рис.3), знайдемо значення змінної величини x, при якій функція (16) досягає максимуму x=4,965.
Рис. 3
Отже,
звідки
тобто, ми одержали закон зміщення Віна.
Таким чином, формула Планка не тільки добре погоджується з експериментальними даними, але й містить у собі дослідні закони теплового випромінювання, а також дозволяє обчислити постійні в законах теплового випромінювання. Отже, формула Планка є повним розв’язком основного завдання теплового випромінювання, поставленого Кірхгофом. Його розв’язування стало можливим лише завдяки революційній квантовій гіпотезі Планка.
|
|
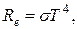 (10)
(10)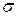 - постійна Стефана-Больцмана. Експериментальне значення постійної Стефана-Больцмана дорівнює
- постійна Стефана-Больцмана. Експериментальне значення постійної Стефана-Больцмана дорівнює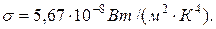
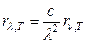 від довжини хвилі λ при різних температурах показані на (рис. 2). Криві мають явно виражений максимум, який із підвищенням температури зміщується у бік більш коротких хвиль.
від довжини хвилі λ при різних температурах показані на (рис. 2). Криві мають явно виражений максимум, який із підвищенням температури зміщується у бік більш коротких хвиль.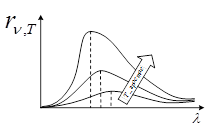
 від λ пропорційна інтегральній випромінювальній здатності Re абсолютно чорного тіла й, за законом Стефана-Больцмана, четвертому степені температури.
від λ пропорційна інтегральній випромінювальній здатності Re абсолютно чорного тіла й, за законом Стефана-Больцмана, четвертому степені температури.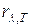 ,від температури Т. Відповідно до цього закону
,від температури Т. Відповідно до цього закону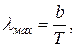 (11)
(11) (12)
(12)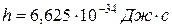 – стала Планка.
– стала Планка.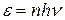 ( n= 0,1,2,…)
( n= 0,1,2,…) (13)
(13)
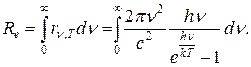
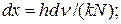
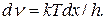 Тут k – стала Больцмана, яка дорівнює 1,38.10-23 Дж/К. З урахуванням цих позначень інтегральна випромінювальна здатність абсолютно чорного тіла Re, буде дорівнювати
Тут k – стала Больцмана, яка дорівнює 1,38.10-23 Дж/К. З урахуванням цих позначень інтегральна випромінювальна здатність абсолютно чорного тіла Re, буде дорівнювати (14)
(14) так як
так як 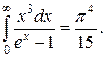
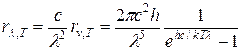 . (15)
. (15)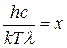 , звідки
, звідки 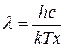 .
.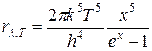 . (16)
. (16)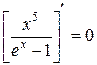 , одержимо
, одержимо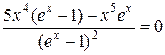 ,
,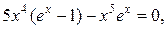 або
або 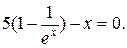
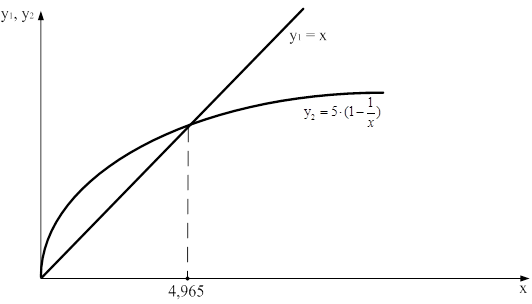
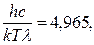
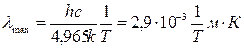 ,
,