|
|
Амплітуда і фаза вимушених коливань (механічних і електромагнітних). Резонанс. Резонансні криві. Параметричний резонансРозглянемо залежність амплітуди А вимушених механічних (6) або електромагнітних (13) коливань від частотиω. Механічні й електромагнітні коливання будемо розглядати одночасно, називаючи коливну величину або зміщенням (х) коливного тіла від положення рівноваги, або зарядом (Q)конденсатора. З формули (6) випливає, що амплітуда А зміщення точок від положення рівноваги має максимум. Щоб визначити резонансну частоту
Ця рівність виконується при двох умовах
Явище різкого зростання амплітуди вимушених коливань при наближенні частоти вимушувальної сили до
На рис. 3 наведені залежності амплітуди вимушених коливань від частоти при різних значеннях коефіцієнта згасання β. З виразів (15) і (16) випливає, що чим менший коефіцієнт β, тим вище і правіше лежить максимум даної кривої. Якщо
Рис.3 У випадку електромагнітних коливань З формули (16) випливає, що при малому згасанні
Поділимо значення резонансної амплітуди (17) на статичне значе-ння амплітуди
де Як видно з (18), добротність коливальної системи характеризує її резонансні властивості. Чим більше число добротності, тим більша резонансна амплітуда.
Рис. 4
Залежність φ від ω при різних коефіцієнтах β графічно показана на рис. 4, з якого випливає, що при зміні ω змінюється і зсув фаз φ. З формули (7) видно, що при ω = 0, φ = 0, а при Зупинимось коротко на явищі параметричного резонансу. Виявляється, що існують інші види зовнішніх взаємодій, з допомогою яких можна значно збільшити амплітуду коливань. Цей вид взаємодій полягає в тому, що в такт коливань періодично змінюють один із параметрів коливальної системи. Так, наприклад, зменшують довжину математичного маятника l, коли він перебуває в крайніх положеннях і дещо збільшують її, коли маятник проходить положення рівноваги, від цього маятник почне сильно розгойдуватись, амплітуда коливань буде швидко зростати, тобто наступить явище параметричного резонансу. Збільшення енергії маятника відбувається за рахунок зміни довжини маятника. Сила натягу нитки маятника в цьому випадку є різною, – меншою в крайніх положеннях і більшою в момент проходження маятником положення рівноваги. При зменшенні довжини маятника (крайні положення) – зовнішні сили виконують від’ємну роботу, а при збільшенні його довжини – додатну. Оскільки додатна робота за модулем є більшою за від’ємну, то сумарна робота за час одного повного коливання (період коливань) є більшою за нуль. Прикладом параметричного резонансу є коливання гойдалки. Без будь-яких зовнішніх впливів дитина, перебуваючи на гойдалці, сама здатна збільшувати амплітуду коливань. Потрібно лише в крайніх положеннях підніматись, а в положенні рівноваги – трохи присідати. В цьому випадку коливальна система поповнюється енергією за рахунок мускульної сили ніг дитини. Явища резонансу можуть бути як шкідливими, так і корисними. Наприклад, при конструюванні машин і різного роду споруд необхідно, щоб їх власна частота коливань не збігалася з частотою можливих зовнішніх впливів, інакше можуть виникнути вібрації, які призведуть до значних руйнувань. З іншого боку, наявність резонансу дозволяє знайти навіть дуже слабкі коливання, якщо їх частота збігається з частотою власних коливань приладу. Так, телебачення, радіотехніка, прикладна акустика, що сприймають електричні коливання, основані на використанні явища резонансу.
Змінний струм Вимушені електромагнітні коливання, які виникають в колі, що містить резистор, котушку індуктивності і конденсатор, можна розглядати як змінний струм. В той же час змінний струм вважають квазістаціонарним, оскільки миттєві значення сили струму в усіх перетинах кола практично однакові. У порівнянні із швидкістю світла будь-які зміни в колі відбуваються досить повільно. Для миттєвих значень квазістаціонарних струмів виконуються закон Ома і правила Кирхгофа. Розглянемо послідовно процеси, які відбуваються в колі, яке містить резистор, котушку індуктивності і конденсатор при вмиканні його до джерела змінної напруги
де
1. Розглянемо коло, в яке ввімкнули лише резистор R, а індуктивність L і ємність С – відсутні (рис.5,а).
Рис.5, а,б При виконанні умови квазістаціонарності струм через резистор R визначається законом Ома:
де амплітуда сили струму дорівнює
На векторній діаграмі (рис. 5,б) показано, що зсув фаз між напругою і струмом в колі, в якому є лише резистор R, дорівнює нулю.
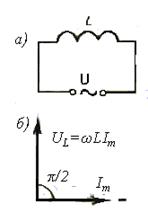
2. Розглянемо випадок, коли змінний струм тече через котушку індуктивностіL, в цьому випадку резистор R і ємність С в колі відсутні(рис. 6,а ). Якщо до кола прикладена змінна напруга (19), то через котушку потече змінний струм, в результаті чого в ній виникне е.р.с. самоіндукції E = Тоді закон Ома для даного замкнутого кола буде мати вигляд
звідки
Рис. 6, а,б
Оскільки зовнішня напруга прикладена до котушки індуктивності, то
визначає спад напруги на котушці. З рівняння (20) випливає, що
або після інтегрування, з урахуванням того, що постійна інтегрування дорівнює нулю, одержимо
де
Величина
називається реактивним індуктивним опором (або індуктивним опором). З виразу (22) випливає, що для постійного струму, коли
Порівнюючи вирази (22) і (24) приходимо до висновку, що спад напруги UL випереджає за фазою струм I, який тече через котушку, на π/2, що й показано на векторній діаграмі (рис. 6, б).
3. Нехай змінний струм у колі тече через конденсатор ємністю С, в цьому випадкуактивний опір R і котушка індуктивності L відсутні,(рис. 7,а).
Рис.7, а,б
Якщо змінна напруга (19) прикладена до конденсатора то, в результаті постійного його перезарядження, у колі потече змінний струм. Оскільки вся зовнішня напруга прикладена до конденсатора, а опором підвідних проводів можна знехтувати, то
Сила струму в цьому випадку буде дорівнювати
де
Величина
Порівнюючи вирази (25) і (26) приходимо до висновку, що спад напруги Uс відстає за фазою від струму, який тече через конденсатор, на π/2. Це показано на векторній діаграмі (рис. 7, б).
4. Розглянемо коло змінного струму, що містить послідовно ввімкнуті резистор, котушку індуктивності і конденсатор. На рис. 8, а показане коло, що містить резистор опором R, котушку індуктивністю L і конденсатор ємністю С, на кінці якого подається зміннанапруга (19). У колі виникне змінний струм, який викличе на всіх елементах кола відповідні спади напруг UR, UL і Uc.На рис. 8,б показана векторна діаграма амплітуд спадів напруг на резисторі UR, котушці
Рис. 8, а,б
Результуюча амплітуда Um прикладеної напруги повинна бути рівною геометричній сумі амплітуд всіх спадів напруг. Як видно з рис. 8,б, кут φ визначає різницю або зсув фаз між напругою і силою струму. З рисунка випливає, що
З прямокутного трикутника, скориставшись теоремою Піфагора, одержуємо, що
звідки амплітуда сили струму буде дорівнювати
Отже, якщо напруга в колі змінюється за законом
то в колі тече струм
де φ і Im визначаються відповідно формулами (27) і (28). Величина
називається повним опором кола змінного струму, а величина
називається реактивним опором. Розглянемо окремий випадок, коли в колі відсутній конденсатор. У цьому випадку спад напруг UR і UL в сумі дорівнює прикладеній напрузі U. Векторна діаграма для даного випадку показана на рис. 9, з якої видно, що
Отже, відсутність конденсатора в колі означає, що
Рис. 9, а,б Даний висновок можна трактувати так: зближаючи обкладки конденсатора до їх повного зіткнення, прийдемо до кола, у якому конденсатор відсутній (відстань між обкладками прямує до нуля, а ємність – до нескінченності. Резонанс напруг Якщо в колі змінного струму, що містить послідовно ввімкнуті конденсатор, котушку індуктивності і резистор (рис. 8,а)
то кут зсуву фаз між струмом і напругою (27) перетворюється в нуль (φ = 0), тобто зміни струму і напруги відбуваються в одній фазі. Умову (32) задовольняє частота
У даному випадку повний опір кола Ζ (30) стає найменшим, рівним активному опору R, а струм у колі визначаючись активним опором, досягає найбільших значень (при даному значенні Um). При цьому спад напруги на активному опорі дорівнює зовнішній напрузі, прикладеній до кола (UR = U), а спади напруг на конденсаторі (Uc) і котушці індуктивності (UL) однакові за амплітудою і протилежні за фазою. Розглянуте явище називається резонансом напруг (послідовним резонансом), тому що при цьому відбувається взаємна компенсація напруг UL і Uc, кожна з яких може значно перевищувати прикладену до кола напругу U. Векторна діаграма для резонансу напруг показана на рис. 9,б. У випадку резонансу напруг
тому, підставивши в цю формулу значення резонансної частоти й амплітуди напруг на котушці індуктивності і конденсаторі, одержимо
де Оскільки добротність звичайних коливальних контурів більша одиниці, то напруга на котушці індуктивності, а також і на конденсаторі перевищує напругу, прикладену до кола. Тому явище резонансу напруг використовується в техніці для підсилення коливання напруги певної частоти. Наприклад, у випадку резонансу на конденсаторі можна одержати напругу з амплітудою
Тема 4. Пружні хвилі |
|
 – частоту, при якій амплітуда А зміщення досягає максимуму, – потрібно дослідити на максимум функцію
– частоту, при якій амплітуда А зміщення досягає максимуму, – потрібно дослідити на максимум функцію 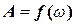 . Диференціюємо підкореневий вираз цієї функції за ω і прирівнюємо його до нуля:
. Диференціюємо підкореневий вираз цієї функції за ω і прирівнюємо його до нуля: ,
,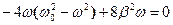
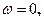 і
і 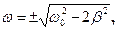 фізичний зміст яких має лише додатне значення. Отже, резонансна частота буде дорівнювати
фізичний зміст яких має лише додатне значення. Отже, резонансна частота буде дорівнювати (15)
(15)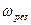 , називається резонансом (відповідно механічним або електричним). У випадку коли
, називається резонансом (відповідно механічним або електричним). У випадку коли 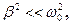 значення
значення 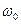 коливної системи. Підставляючи (15) у формулу (6), одержимо
коливної системи. Підставляючи (15) у формулу (6), одержимо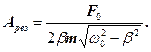 (16)
(16) , то всі криві (див. рис.3) сходяться в одній точці, яка відповідає, відмінному від нуля граничному значенню амплітуди
, то всі криві (див. рис.3) сходяться в одній точці, яка відповідає, відмінному від нуля граничному значенню амплітуди 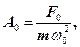 так званому статичному відхиленню.
так званому статичному відхиленню.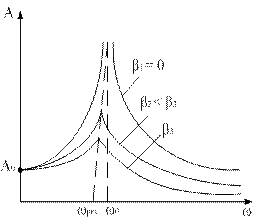
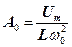 . Якщо
. Якщо 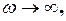 то всі криві мають асимптотичне наближення до нуля. Показані на рис. 3 криві називаються резонансними кривими.
то всі криві мають асимптотичне наближення до нуля. Показані на рис. 3 криві називаються резонансними кривими. резонансна амплітуда зміщення буде мати вигляд
резонансна амплітуда зміщення буде мати вигляд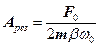 . (17)
. (17)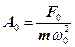 , одержимо добротність коливальної системи
, одержимо добротність коливальної системи (18)
(18) ─ логарифмічний декремент згасання.
─ логарифмічний декремент згасання.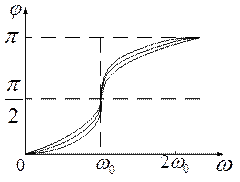
 незалежно від значення коефіцієнта згасання β, φ = π/2, тобто сила випереджає за фазою коливання на π/2. При подальшому збільшенні ω зсув фаз зростає і при
незалежно від значення коефіцієнта згасання β, φ = π/2, тобто сила випереджає за фазою коливання на π/2. При подальшому збільшенні ω зсув фаз зростає і при  ,
,  , тобто фаза коливань майже протилежна до фази зовнішньої сили. Сімейство кривих, зображених на рис. 4, називається фазовими резонансними характеристиками.
, тобто фаза коливань майже протилежна до фази зовнішньої сили. Сімейство кривих, зображених на рис. 4, називається фазовими резонансними характеристиками.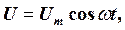 (19)
(19)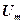 –амплітуда напруги.
–амплітуда напруги.
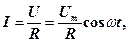
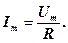
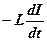 .
.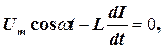
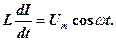 (20)
(20)
 (21)
(21)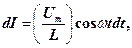
 (22)
(22)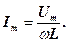
 (23)
(23) , котушка індуктивності опору не чинить. Підстановка значення
, котушка індуктивності опору не чинить. Підстановка значення  у вираз (20) з врахуванням (21) приводить до наступного значення спаду напруги на котушці індуктивності:
у вираз (20) з врахуванням (21) приводить до наступного значення спаду напруги на котушці індуктивності: (24)
(24)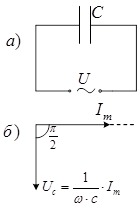
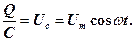
 (25)
(25)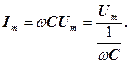
 називається реактивним або ємнісним опором. Для постійного струму (ω = 0) Rc =
називається реактивним або ємнісним опором. Для постійного струму (ω = 0) Rc = 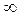 , тобто постійний струм через конденсатор текти не може. Спад напруги на конденсаторі у нашому випадку буде дорівнювати
, тобто постійний струм через конденсатор текти не може. Спад напруги на конденсаторі у нашому випадку буде дорівнювати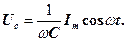 (26)
(26) і конденсаторі Uc.
і конденсаторі Uc.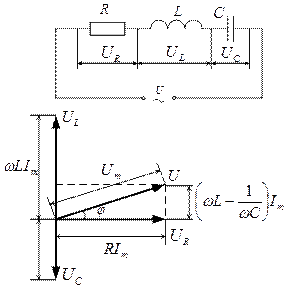
 (27)
(27)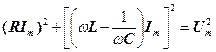 ,
, (28)
(28)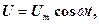
 (29)
(29) (30)
(30)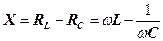
 (31)
(31) , а не С =0.
, а не С =0.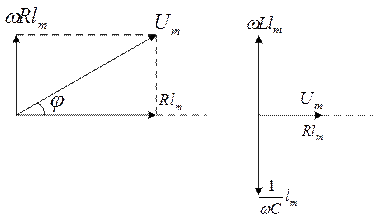
 (32)
(32)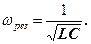
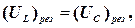

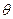 - добротність контуру.
- добротність контуру.