|
|
Материалы текущего, промежуточного и итогового контроляФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ФГОУ ВПО «Волгоградская академия государственной службы» Кафедра информационных систем и математического моделирования И. П. Мединцева Канд. пед. наук, доцент УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС МатематиКА для студентов специальности 030301 «Психология», Подготовки бакалавра по направлению 030300.62 «Психология»
Волгоград 2009 Содержание
Раздел 1. Рабочая программа учебной дисциплины...................................................................... 3 1.1. Требования образовательного стандарта по учебной дисциплине «Математика».......... 3 1.2. Цели и задачи учебной дисциплины..................................................................................... 3 1.3. Требования к уровню освоения дисциплины....................................................................... 3 1.4. Тематический план курса «Математика» (136 ч) для студентов П-100............................. 4 1.5. Учебно-методическое обеспечение учебной дисциплины................................................. 5 Темы, выносимые на самостоятельное изучение...................................................................... 12 Вопросы к зачету (часть 1)........................................................................................................... 13 Вопросы к экзамену (часть 2)...................................................................................................... 15 Список рекомендуемой литературы........................................................................................... 16 Материалы текущего, промежуточного и итогового контроля............................................... 17 Раздел 2. Методические рекомендации по изучению учебной дисциплины для студентов... 23 2.1. Рекомендации по использованию материалов учебно-методического комплекса........ 23 2.2. Пожелания к изучению отдельных тем курса.................................................................... 24 2.3. Рекомендации по работе с литературой.............................................................................. 24 2.4. Разъяснения по поводу работы с тестовой системой курса и практическими задачами 25 2.5. Советы по подготовке к зачету и экзамену........................................................................ 26 Раздел 3. Материалы тестовой системы или практических заданий по темам лекций........... 26 Раздел 4. Словарь основных терминов (глоссарий)..................................................................... 67
Раздел 1. Рабочая программа учебной дисциплины 1.1. Требования образовательного стандарта по учебной дисциплине «Математика» Введение в дискретную математику; элементы теории множеств; векторная алгебра; матрицы; элементы функционального анализа; вероятность и статистика; теория вероятностей; статистическое оценивание и проверка гипотез; параметрические и непараметрические методы; элементы дисперсионного анализа; статистические методы обработки экспериментальных данных. 1.2. Цели и задачи учебной дисциплины Цель изучения дисциплины «Математика» состоит в освоении студентами основ математического аппарата, развитии логического и алгоритмического мышления, выработке умения самостоятельно расширять математические знания и проводить анализ прикладных задач. Основными задачами данного учебного курса являются: – формирование представлений об основных математических понятиях и методах; – формирование умений решать прикладные задачи на основе базового математического аппарата. В первой части курса рассматриваются элементы теории множеств, математического анализа и линейной алгебры, во второй — теории вероятностей и математической статистики. Распределение времени по видам учебных занятий произведено с учетом сложности изучаемых вопросов, требуемой глубины изучения, а также необходимого уровня математической подготовки студентов. Математика является фундаментальной дисциплиной, имеющей важное значение для успешного изучения специальных дисциплин, которые предусмотрены учебными планами специальности «Психология». 1.3. Требования к уровню освоения дисциплины В результате изучения предмета «Математика» студент должен иметь представление: – о математике как особом способе познания мира; – о месте и роли математики в современном мире, мировой культуре и истории; – о роли математики в гуманитарных исследованиях. Студент, прошедший курс обучения, должен знать основные понятия и методы математического анализа, линейной алгебры, дискретной математики, векторной алгебры, методы теории вероятностей и математической статистики и уметь их использовать для решения практических задач. Студент должен приобрести навыки: – употребления математической символики для выражения количественных и качественных отношений объектов; – использования основных приемов обработки и обобщения данных. 1.4. Тематический план курса «Математика» (136 ч) для студентов П-100
1.5. Учебно-методическое обеспечение учебной дисциплины ЛЕКЦИИ ЧАСТЬ I. Лекция 1.Матрицы. Матрицы. Виды матриц. Действия над матрицами: сложение, умножение на число, произведение матриц. Лекция 2. Определители. Определители второго и третьего порядка. Свойства определителей. Миноры и алгебраические дополнения. Разложение определителя по элементам какого-либо столбца или строки. Понятие об определителе n-го порядка. Лекция 3. Обратная матрица. Вырожденная матрица, невырожденная матрица. Обратная матрица. Методы вычисления обратной матрицы: метод присоединенной матрицы, метод элементарных преобразований. Лекция 4.Ранг матрицы. Ранг матрицы. Методы вычисления ранга матрицы: метод окаймляющих миноров, метод элементарных преобразований. Лекция 5. Системы линейных уравнений. Формулы Крамера. Системы линейных уравнений. Однородные и неоднородные системы линейных уравнений. Решение системы линейных уравнений. Совместные и несовместные системы. Определенные и неопределенные системы. Формулы Крамера. Матричная запись системы линейных уравнений и ее решение. Лекция 6.Системы линейных уравнений. Метод Гаусса. Система n линейных уравнений с n неизвестными. Метод Гаусса. Лекция 7.Системы линейных уравнений. Исследование совместности. Решение произвольных систем. Теорема Кронекера-Капелли. Исследование совместности систем линейных уравнений. Метод Жордана-Гаусса. Общее решение системы. Лекция 8.Введение в теорию множеств. Понятие множества. Способы задания множеств. Операции над множествами: объединение, пересечение, разность, дополнение множеств. Универсальное множество. Диаграммы Венна. Лекция 9.Функции одной переменной. Понятие функции. Способы задания функции. Область определения и множество значений функции. Классификация функций. График функции. Основные элементарные функции и их графики. Лекция 10. Предел функции. Последовательности. Предел последовательности. Предел функции. Теоремы о пределах. Бесконечно малые и бесконечно большие величины. Два замечательных предела. Односторонние пределы. Сравнение бесконечно малых. Лекция 11. Непрерывность функции. Приращение аргумента и функции. Непрерывность функции. Точки разрыва и их классификация. Действия над непрерывными функциями. Лекция 12. Дифференциальное исчисление функции одной переменной. Задачи, приводящие к понятию производной. Производная функции, ее геометрический смысл. Правила дифференцирования. Производные основных элементарных функций. Дифференцирование сложных функций. Дифференцирование неявных функций. Дифференцирование функций, заданных параметрически. Логарифмическое дифференцирование. Лекция 13. Дифференциальное исчисление функции одной переменной. Дифференциал функции. Геометрический смысл дифференциала. Дифференциал суммы, произведения и частного. Лекция 14. Дифференциальное исчисление функции одной переменной. Приложения производной. Правило Лопиталя для раскрытия неопределенностей. Теоремы Ролля и Лагранжа. Применение производной к исследованию функций. Возрастание и убывание функции. Экстремум. Отыскание наибольшего и наименьшего значений непрерывной на отрезке функции. Выпуклость и вогнутость. Точки перегиба. Асимптоты. Схема исследования функций и построение графиков. Лекция 15. Интегральное исчисление функции одной переменной. Первообразная. Неопределенный интеграл, его свойства. Таблица основных формул интегрирования. Непосредственное интегрирование. Метод замены переменной. Метод интегрирования по частям. Лекция 16. Интегральное исчисление функции одной переменной. Определенный интеграл. Формула Ньютона-Лейбница. Свойства определенного интеграла. Замена переменной в определенном интеграле. Интегрирование по частям. Лекция 17. Интегральное исчисление функции одной переменной. Несобственные интегралы. Интегралы с бесконечными пределами. Интегралы от неограниченных функций. ЧАСТЬ II. Лекция 1.Предмет теории вероятностей. Основные понятия теории вероятностей. Предмет теории вероятностей и краткая историческая справка. Событие, вероятность события, свойства вероятности. Достоверные и невозможные события. Несовместные события. Совместные события. Противоположные события. Равновозможные события. Полная группа событий. Благоприятствующие случаи. Классическое определение вероятности. Лекция 2. Основные формулы комбинаторики. Правило умножения, правило сложения. Основные формулы комбинаторики: перестановки, размещения, сочетания. Лекция 3.Основные теоремы теории вероятностей. Сумма событий. Произведение событий. Теорема сложения вероятностей. Зависимые события, независимые события. Условная вероятность. Теорема умножения вероятностей. Лекция 4.Формула полной вероятности. Формула Байеса. Гипотезы. Формула полной вероятности, формула Байеса. Лекция 5. Формула Бернулли. Повторение испытаний. Формула Бернулли. Повторение испытаний. Наивероятнейшее число наступлений события. Лекция 6.Асимптотические формулы. Локальная теорема Лапласа, интегральная теорема Лапласа, формула Пуассона. Лекция 7.Случайные величины. Случайная величина. Закон распределения вероятностей случайных величин. Дискретные и непрерывные случайные величины. Способы задания закона распределения вероятностей дискретной случайной величины. Функция распределения, ее свойства. Многоугольник распределения. Лекция 8.Математическое ожидание дискретной случайной величины. Математические операции над случайными величинами. Математическое ожидание дискретной случайной величины, свойства математического ожидания. Лекция 9.Дисперсия дискретной случайной величины. Дисперсия дискретной случайной величины. Формула для вычисления дисперсии, свойства дисперсии. Лекция 10.Непрерывные случайные величины. Числовые характеристики непрерывной случайной величины. Непрерывные случайные величины. Интегральная функция распределения, ее свойства. Дифференциальная функция распределения, ее свойства. Математическое ожидание непрерывной случайной величины. Дисперсия непрерывной случайной величины. Лекция 11. Законы распределения случайной величины. Законы распределения дискретной случайной величины: биномиальное распределение, распределение Пуассона, геометрическое и гипергеометрическое распределения. Лекция 12. Законы распределения случайной величины. Законы распределения непрерывной случайной величины: равномерное, показательное распределение. Лекция 13.Нормальный закон распределения. Нормальный закон распределения. Числовые характеристики нормального закона. Функция Лапласа. Вычисление вероятности попадания нормальной случайной величины на заданный интервал. Вероятность заданного отклонения нормальной случайной величины от ее среднего значения. Правило трех сигм. Формулировка центральной предельной теоремы. Лекция 14.Предмет математической статистики. Математическая статистика. Предмет математической статистики. Задачи математической статистики. Выборочный метод. Генеральная и выборочная совокупности. Лекция 15.Статистическое распределение выборки. Варианты, частоты, относительные частоты. Вариационный ряд. Статистическое распределение выборки. Эмпирическая функция распределения. Полигон, гистограмма. Выборочное среднее, выборочная дисперсия. Мода, медиана, размах выборки. Лекция 16. Регрессионный анализ. Регрессионный анализ. Выбор регрессионной модели, уравнение регрессии. Отыскание параметров уравнения прямой линии регрессии по несгруппированным данным. Лекция 17. Регрессионный анализ. Отыскание параметров уравнения прямой линии регрессии по сгруппированным данным. Лекция 18.Корреляционный анализ. Корреляционный анализ. Формула для вычисления коэффициента корреляции, свойства коэффициента корреляции. Таблица Чеддока. Семинарские занятия ЧАСТЬ I. Семинар 1.Матрицы. Матрицы. Действия над матрицами: сложение, умножение на число, произведение матриц. Семинар 2. Определители. Определители второго и третьего порядка. Миноры и алгебраические дополнения. Разложение определителя по элементам какого-либо ряда. Понятие об определителе n-го порядка. Семинар 3. Обратная матрица. Методы вычисления обратной матрицы: метод элементарных преобразований, метод присоединенной матрицы. Семинар 4.Ранг матрицы. Ранг матрицы. Методы вычисления ранга матрицы: метод окаймляющих миноров, метод элементарных преобразований. Семинар 5. Системы линейных уравнений. Формулы Крамера. Решение систем линейных уравнений. Формулы Крамера. Матричная запись системы линейных уравнений и ее решение. Семинар 6.Системылинейных уравнений. Метод Гаусса. Решение системлинейных уравнений. Метод Гаусса. Семинар 7.Системы линейных уравнений. Исследование совместности. Системы линейных уравнений. Теорема Кронекера-Капелли. Исследование совместности систем линейных уравнений. Базисные решения. Семинар 8.Введение в теорию множеств. Понятие множества. Способы задания множеств. Операции над множествами: объединение, пересечение, разность, дополнение множеств. Универсальное множество. Диаграммы Венна. Семинар 9.Функции одной переменной. Понятие функции. Способы задания функции. Область определения и множество значений функции. Классификация функций. График функции. Основные элементарные функции. Семинар 10.Предел функции. Предел функции. Теоремы о пределах. Односторонние пределы. Два замечательных предела. Нахождение пределов функций. Раскрытие неопределенностей. Семинар 11. Дифференциальное исчисление функции одной переменной. Производная функции, ее геометрический смысл. Правила дифференцирования. Производные основных элементарных функций. Дифференцирование сложных функций. Дифференцирование неявных функций. Дифференцирование функций, заданных параметрически. Логарифмическое дифференцирование. Семинар 12.Правило Лопиталя для раскрытия неопределенностей. Вычисление пределов функции с использованием правила Лопиталя. Семинар 13. Дифференциальное исчисление функции одной переменной. Исследование функций и построение графиков. Возрастание и убывание функции. Экстремум. Отыскание наибольшего и наименьшего значения непрерывной на отрезке функции. Выпуклость и вогнутость. Точки перегиба. Асимптоты. Семинар 14. Интегральное исчисление функции одной переменной. Первообразная. Неопределенный интеграл, его свойства. Таблица основных формул интегрирования. Непосредственное интегрирование. Метод замены переменной. Метод интегрирования по частям. Семинар 15. Интегральное исчисление функции одной переменной. Определенный интеграл. Формула Ньютона-Лейбница. Свойства определенного интеграла. Замена переменной в определенном интеграле. Интегрирование по частям. Семинар 16. Интегральное исчисление функции одной переменной. Несобственные интегралы. Интегралы с бесконечными пределами. Интегралы от неограниченных функций. ЧАСТЬ II. Семинар 1. Классическое определение вероятности. Классическое определение вероятности. Непосредственный подсчет вероятностей. Семинар 2.Классическое определение вероятности. Классическое определение вероятности. Непосредственный подсчет вероятностей. Семинар 3.Основные формулы комбинаторики. Формулы комбинаторики. Размещения, перестановки, сочетания. Правило умножения и сложения. Семинар 4.Основные теоремы теории вероятностей. Сумма и произведение событий. Вероятность суммы событий. Вероятность произведения событий. Семинар 5. Основные теоремы теории вероятностей. Сумма и произведение событий. Вероятность суммы событий. Вероятность произведения событий. Семинар 6. Формула полной вероятности. Формула Байеса. Формула полной вероятности. Формула Байеса. Семинар 7. Формула Бернулли. Повторение испытаний. Формула Бернулли. Наивероятнейшее число наступления события. Семинар 8. Асимптотические формулы. Локальная теорема Лапласа, интегральная теорема Лапласа, формула Пуассона. Семинар 9. Случайные величины. Случайные величины. Дискретные случайные величины. Закон распределения дискретной случайной величины. Ряд распределения. Многоугольник распределения, функция распределения. Семинар 10. Числовые характеристики дискретной случайной величины. Числовые характеристики дискретной случайной величины: математическое ожидание, дисперсия. Семинар 11. Непрерывные случайные величины. Непрерывные случайные величины. Интегральная функция распределения, ее свойства. Дифференциальная функция распределения, ее свойства. Семинар 12. Числовые характеристики непрерывной случайной величины. Числовые характеристики непрерывной случайной величины: математическое ожидание, дисперсия. Семинар 13.Законы распределения случайной величины. Законы распределения дискретной случайной величины: биномиальное распределение, распределение Пуассона, геометрическое и гипергеометрическое распределение. Законы распределения непрерывной случайной величины: равномерное, показательное распределение. Семинар 14. Нормальный закон распределения. Нормальный закон распределения. Вероятность попадания нормальной случайной величины в заданный интервал. Вероятность заданного отклонения нормальной случайной величины от ее среднего значения. Семинар 15.Статистическое распределение выборки. Выборка. Статистический ряд. Полигон. Гистограмма. Эмпирическая функция распределения. Выборочное среднее, выборочная дисперсия. Мода, медиана, размах выборки. Семинар 16. Корреляционный и регрессионный анализ. Корреляционный и регрессионный анализ. Уравнение регрессии. Отыскание параметров уравнения прямой линии регрессии по несгруппированным данным. Коэффициент корреляции. Семинар 17.Корреляционный и регрессионный анализ. Корреляционный и регрессионный анализ. Уравнение регрессии. Отыскание параметров уравнения прямой линии регрессии по сгруппированным данным. Коэффициент корреляции. Темы, выносимые на самостоятельное изучение Тема:Векторы. Скалярное, векторное и смешанное произведение векторов. Вопросы: Векторы. Разложение вектора по осям координат. Координаты вектора. Сложение и вычитание векторов. Умножение вектора на число. Скалярное, векторное и смешанное произведение векторов, их основные свойства и выражения в координатной форме. Контрольное задание по теме:Законспектировать ответы на контрольные вопросы. Форма отчетности:Выполнить контрольное задание по теме и показать преподавателю результат. Рекомендуемая литература: 1. Данко П.Е., Попов А.Г., Кожевникова Т.Я.. Высшая математика в упражнениях и задачах. Ч.1, 2. – Москва: Высшая школа, 1999. 2. Демидович Б.П. Краткий курс высшей математики. – 2004. Тема:Элементы математической логики. Вопросы: Сущность математической логики. Высказывание. Элементарное высказывание. Булевы функции. Основные операции: отрицание, дизъюнкция, конъюнкция, импликация, эквивалентность. Таблица истинности. Равносильные функции. Основные равносильности. Предикаты. Квантор всеобщности. Квантор существования. Контрольное задание по теме:Законспектировать ответы на контрольные вопросы. Форма отчетности:Выполнить контрольное задание по теме и показать преподавателю результат. Рекомендуемая литература: 1. Грес П.В. Математика для гуманитариев: Учеб. пособие. – М.: Юрайт, 2000. – 112 с. 2. Москинова Г.И. Дискретная математика. Математика для менеджера в примерах и упражнениях: Учеб. пособие. – М.: Логос, 2000. – 240 с. Тема:Основные понятия теории графов. Вопросы: Основные понятия (граф, ребра, дуги). Способы задания графов. Операции над частями графа. Маршруты и деревья. Контрольное задание по теме:Законспектировать ответы на контрольные вопросы. Форма отчетности:Выполнить контрольное задание по теме и показать преподавателю результат. Рекомендуемая литература: 1. Грес П.В. Математика для гуманитариев: Учеб. пособие. – М.: Юрайт, 2000. – 112 с. 2. Москинова Г.И. Дискретная математика. Математика для менеджера в примерах и упражнениях: Учеб. пособие. – М.: Логос, 2000. – 240 с. Тема: Испытание гипотез. Вопросы: Испытание гипотез. Процедура испытания гипотез. Односторонняя и двусторонняя проверки. Статистика. Контрольное задание по теме:Законспектировать ответы на контрольные вопросы. Форма отчетности:Выполнить контрольное задание по теме и показать преподавателю результат. Рекомендуемая литература: 1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – 1998. 2. Просветов Г.И. Математика: Задачи и решения. – М.: Изд-во РДЛ, 2005. – 208 с. Вопросы к зачету (часть 1) 1. Понятие множества. Способы задания множеств. Операции над множествами: объединение, пересечение, разность, дополнение множеств. Универсальное множество. Диаграммы Венна. 2. Определители второго и третьего порядка. Свойства определителей. 3. Миноры и алгебраические дополнения. Разложение определителя по элементам какого-либо ряда. Понятие об определителе n-го порядка. 4. Матрицы. Виды матриц. Действия над матрицами: сложение матриц, умножение матрицы на число, произведение матриц. 5. Обратная матрица. Методы вычисления обратной матрицы: метод присоединенной матрицы, метод элементарных преобразований. 6. Системы линейных уравнений. Однородные и неоднородные системы линейных уравнений. Решение системы линейных уравнений. Совместные и несовместные системы. Определенные и неопределенные системы. 7. Система n линейных уравнений с n неизвестными Формулы Крамера. 8. Матричная запись системы линейных уравнений. Решение системы линейных уравнений в матричной форме. 9. Ранг матрицы. Методы вычисления ранга матрицы: метод окаймляющих миноров, метод элементарных преобразований. 10. Решение произвольных систем. Теорема Кронекера-Капелли. Исследование совместности систем линейных уравнений. Метод Жордана-Гаусса. 11. Понятие функции. Способы задания функции. Область определения и множество значений функции. Классификация функций. График функции Простейшие элементарные функции. 12. Предел функции. Теоремы о пределах. Два замечательных предела. 13. Приращение аргумента и функции. Непрерывность функции. Точки разрыва и их классификация. Действия над непрерывными функциями. 14. Производная функции, ее геометрический смысл. 15. Правила дифференцирования. Производные основных элементарных функций. 16. Дифференцирование сложных функций; дифференцирование функций заданных параметрически; дифференцирование неявных функций; логарифмическое дифференцирование. 17. Дифференциал функции, его геометрический смысл. Дифференциал суммы, произведения, частного. 18. Правило Лопиталя для раскрытия неопределенностей. 19. Применение производной к исследованию функций. Схема исследования функций и построение графиков. 20. Возрастание и убывание функции. Экстремум функции. Необходимые условия экстремума. Достаточные признаки существования экстремума. 21. Выпуклость и вогнутость. Точки перегиба. 22. Асимптоты: вертикальные, горизонтальные, наклонные. 23. Наименьшее и наибольшее значения функции на отрезке. 24. Первообразная. Неопределенный интеграл. Геометрический смысл неопределенного интеграла. Свойства неопределенного интеграла. 25. Таблица основных интегралов. 28. Основные приемы интегрирования: непосредственное интегрирование; метод замены переменной, метод подстановки; интегрирование по частям. 29. Определенный интеграл. Геометрический смысл определенного интеграла. Свойства определенного интеграла. 30. Формула Ньютона-Лейбница. 31. Замена переменной в определенном интеграле. Интегрирование по частям. Вопросы к экзамену (часть 2) 1. Предмет теории вероятностей. 2. Событие. Элементарные события, составные события. Противоположное событие. Достоверное и невозможное события. Совместные и несовместные события. 3. Вероятность. Классическое определение вероятности. Свойства вероятности. 4. Формулы комбинаторики: перестановки, размещения, сочетания. Правило умножения, правило сложения. 5. Сумма событий. Вероятность суммы событий. 6. Произведение событий. Условная вероятность. Зависимые и независимые события. Вероятность произведения событий. 7. Формула полной вероятности. Формула Байеса. 8. Повторение испытаний. Формула Бернулли. Наивероятнейшее число наступлений события. 9. Асимптотические формулы. Локальная теорема Лапласа, интегральная теорема Лапласа, формула Пуассона. 10. Случайные величины. Дискретные и непрерывные случайные величины (определения, примеры). 11. Закон распределения вероятностей дискретной случайной величины. Ряд распределения. Функция распределения, ее свойства. Многоугольник распределения. 12. Биномиальное распределение. 13. Распределение Пуассона. 14. Геометрическое распределение. 15. Гипергеометрическое распределение. 16. Математические операции над случайными величинами. 17. Математическое ожидание дискретной случайной величины. Свойства математического ожидания. 18. Дисперсия дискретной случайной величины. Формула для вычисления дисперсии. Свойства дисперсии. 19. Непрерывные случайные величины. Интегральная функция распределения, ее свойства. 20. Непрерывные случайные величины. Дифференциальная функция распределения (плотность распределения), ее свойства. 21. Числовые характеристики непрерывных случайных величин: математическое ожидание, дисперсия. 22. Нормальное распределение. График нормальной кривой. Вероятность попадания нормальной величины в заданный интервал. Вероятность отклонения нормальной случайной величины от ее среднего значения. Правило трех сигм. Центральная предельная теорема. 23. Равномерное распределение. Плотность вероятности равномерного распределения. Функция распределения. Основные числовые характеристики равномерно распределенной величины. 24. Показательное распределение. Плотность вероятности показательного распределения. Функция распределения. Основные числовые характеристики непрерывной случайной величины, имеющей показательное распределение. 25. Предмет математической статистики. Задачи математической статистики. 26. Генеральная совокупность. Выборка. Варианты, частоты, относительные частоты. Вариационный ряд. Статистический ряд частот, относительных частот. Интервальный статистический ряд. 27. Эмпирическая функция распределения. Полигон. Гистограмма. 28. Выборочные среднее, дисперсия; мода, медиана, размах выборки. 29. Регрессионный анализ. Уравнение регрессии. Отыскание параметров уравнения регрессии по несгруппированным и сгруппированным данным. 30. Корреляционный анализ. Коэффициент линейной корреляции, его свойства. Список рекомендуемой литературы Основная литература: 1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – 1998. 2. Горбатов В.А. Фундаментальные основы дискретной математики. Информационная математика. – 2000. 3. Данко П.Е., Попов А.Г., Кожевникова Т.Я.. Высшая математика в упражнениях и задачах. Ч.1, 2. – Москва: Высшая школа, 1999. 4. Демидович Б.П. Краткий курс высшей математики. – 2004. 5. Кириллов А.Л. Введение в математический анализ элементарных функций. Сев.-Зап. акад. гос. службы (СЗАГС). – 1998. 6. Кремер Н.Ш. Теория вероятностей и математическая статистика. – 2001. 7. Математика. О.А. Астафурова, Н.И. Меркулова, М.Н. Назаров, М.П. Харламов, Е.Г. Шведов; Под ред. Н.И. Меркуловой. – 2000. 8. Математика. Е.Н. Малышева, И.П. Мединцева, Н.И. Меркулова, М.П. Харламов, Е.Г. Шведов; Под ред. Н.И. Меркуловой. – 2001. 9. Ротарь В.И. Теория вероятностей. – 1992. 10. Шипачев В.С. Высшая математика. – 2000. 11. Шипачев В.С. Задачник по высшей математике. – 2001. Дополнительная литература: 1. Абрашин Е.А., Молоканова Н.Е. Методическое пособие по высшей математике для студентов заочной формы обучения. – Волгоград: ВАГС, 1996. 2. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1997. 3. Калинина В.Н., Панкин В.Ф. Математическая статистика. – М.: Высшая школа, 1994. 4. Сборник задач по математике для втузов. Ч. 1, 2. Под ред. Ефимова А.В., Демидовича Б.П. – Москва: Наука, 1986. Материалы текущего, промежуточного и итогового контроля Вопросы для проведения внутрисеместровой аттестации 1. Множества. Операции над множествами. 2. Матрицы. Действия с матрицами. 3. Обратная матрица. Способы нахождения обратной матрицы. 4. Ранг матрицы. Способы вычисления ранга матрицы. 5. Определители. Способы вычисления определителей. 6. Системы линейных уравнений. 7. Формулы Крамера. 8. Метод последовательных исключений Гаусса. 9. Матричный способ решения систем линейных уравнений. Варианты контрольных работ для осуществления текущего контроля уровня знаний студентов Контрольная работа №1 1. Вычислить определитель, приведя его к удобному:
2. Найти обратную матрицу для матрицы А:
3. Вычислить
4. Вычислить ранг матрицы
5. Решить систему линейных уравнений с помощью формул Крамера:
6. Исследовать систему на совместность и решить ее, если она совместна: а) Контрольная работа №2 1. Найти пределы функций:
2. Найти производные функций:
3. Найти пределы функций, пользуясь правилом Лопиталя:
4. Исследовать методами дифференциального исчисления и на основании исследования построить графики функций: |
|
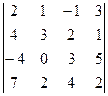

 , где
, где
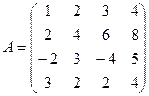

 б)
б) 

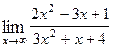







 ,
,
 ,
,
 ,
,
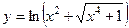 ,
,
 ,
,
 .
.
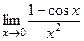 ,
,
 .
.