|
|
Раздел 3. Материалы тестовой системы или практических заданий по темам лекцийПрактические задания к теме «Матрицы» Пример 1. Найти матрицу 3A для матрицы A = Решение. По определению, при умножении матрицы на число каждый элемент матрицы умножается на это число:
Пример 2. Найти сумму и разность матриц A и B, если
Решение. Так как количество строк и столбцов матрицы A равно количеству строк и столбцов матрицы B, то их сумма и разность возможны:
Пример 3. Найти AB и BA, если
Решение. Так как обе матрицы квадратные и одной размерности, то их можно перемножать в любом порядке:
Как показывает этот пример, AB ¹ BA. Ответ: Пример 4. Найти AB и BA, если
Решение. а) Так как число столбцов матрицы A равно числу строк матрицы B, то произведение AB возможно:
б) Произведение BA невозможно, т. к. число столбцов первой матрицы B не равно числу строк второй матрицы A. Ответ: Практические задания к теме «Определители» Пример 1. Вычислить определитель Решение. Пример 2. Вычислить определитель а) по правилу "треугольников"; б) разложив его по элементам первого столбца; в) превратив его в "удобный". Решение: а) По правилу "треугольников"
б) Разложим заданный определитель по элементам первого столбца, которые равны a11= 1, a21= 2, a31 = 3. Вычислим алгебраические дополнения этих элементов:
Итак, a11×A11 + a21× A21+ a31 × A31= 1 × 5 +2 × (‑10) + 3 × 0 = ‑15. в) Превратим заданный определитель в "удобный".
Ответ: ‑15. Пример 3. Вычислить определитель четвёртого порядка
Решение. Превратим определитель в удобный. Для этого из второго столбца вычтем третий, тогда получим:
Затем из третьего столбца вычтем удвоенный первый:
Из четвёртого столбца вычтем утроенный первый:
Разложим этот определитель по элементам 1-й строки:
Сложим второй и третий столбцы, получим:
Из второго столбца вычтем утроенный первый и разложим определитель по элементам третьей строки:
Ответ: 296. Практические задания к теме «Обратная матрица» Пример 1. Дана матрица А= Решение. Вычисляем определитель матрицы А
Следовательно, матрица невырожденная и для нее существует обратная. Находим алгебраические дополнения
Следовательно, Пример 2. Найти матрицу, обратную матрице A = Сделать проверку. Решение. Обратная матрица имеет вид:
Нужно сделать проверку, используя то свойство, что произведение заданной матрицы A и найденной обратной A‑1должно равняться единичной матрице, т. е. A × A-1= E.
следовательно, обратная матрица найдена верно. Ответ: Практические задания к теме «Ранг матрицы» Пример 1. Определить ранг матрицы Решение. Сложим соответствующие элементы 1-й и 3-й строк
Разделим на 4 элементы 1-й строки
Из элементов 1-й строки вычтем соответствующие элементы 2-й строки и вычеркнем 1-ю строку
Ранг последней матрицы равен 2, т.к., например, Ответ: r(A) = 2 Пример 2.Определить ранг матрицы Решение. В левом верхнем углу матрицы минор второго порядка отличен от нуля Как видно, они нулевые, поэтому r(А)=2. Практические задания к теме «Системы линейных уравнений» Пример 1. Методом Гаусса решить систему уравнений:
Решение.Расширенная матрица системы имеет вид:
Шаг 1. Так как a11 ¹ 0, то, умножая первую строку матрицы на числа (‑2), (‑4) и прибавляя полученные строки соответственно ко второй и третьей строкам, исключим переменную x1 из второй и третьей строки
Шаг 2. Учитывая, что a22 = ‑7¹ 0, умножаем вторую строку на (‑1) и прибавляем ее к третьей. Получим:
Итак, уравнение, соответствующее третьей строке последней матрицы, свелось к неверному равенству 0 = ‑1, следовательно, данная система несовместна. Пример 2. Решить систему в матричной форме
Решение. Введём обозначения матриц:
тогда решение системы в матричной форме запишется как Система линейных уравнений имеет единственное решение, если |A| ¹ 0. Вычислим этот определитель:
Матрица A невырожденная, следовательно, система имеет единственное решение. Для решения системы линейных уравнений нам требуется найти матрицу, обратную к матрице A:
Вычислим алгебраические дополнения элементов матрицы A':
Следовательно, присоединённая матрица имеет вид:
Тогда обратная матрица
Теперь, зная обратную матрицу, найдем решение системы:
Итак, x1 = 1, x2 = 1, x3 = 2. Сделаем проверку, подставив найденные значения неизвестных в каждое уравнение исходной системы:
Уравнения обратились в тождества, значит, неизвестные найдены правильно. Ответ: Пример 3. Решить систему, используя формулы Крамера:
Решение. Вычислим основной определитель системы (определитель, составленный из коэффициентов при неизвестных)
значит, система имеет единственное решение. Вычисляем другие определители:
Находим неизвестные:
Сделаем проверку:
Уравнения обратились в тождества, значит, неизвестные найдены верно. Ответ: Пример 4.Исследовать систему уравнений
Решение. Расширенная матрица системы имеет вид
Прибавим элементы второй строки к соответствующим элементам первой и четвертой строк. Затем разделим элементы первой строки на 4, а элементы четвертой строки на 5: Вычтем из элементов третьей строки соответствующие элементы первой строки, а из элементов пятой строки вычтем элементы четвертой строки; после этого вычеркнем третью и пятую строки:
Найдем определитель последней матрицы:
Следовательно, r(A) = 3. Ранг расширенной матрицы также равен 3, так как найденный определитель является минором матрицы B. Итак, система совместна. Для ее решения возьмем, например, первое, третье и пятое уравнения:
Отсюда, выразив одни переменные через другие, найдем, что x1 = 1, x2 = 2, x3 = 3. Практические задания к теме «Множества» 1. Описать перечислением элементов множество: A = {xÎZ: (x – 3)(x2 – 1) = 0 и x ³ 0} A = {xÎR: A = {xÎN: 2. Пусть A = (–1; 2], B = [1; 4). Найти множества AÈB, AÇB, A\B, B\A и изобразить их на числовой оси. 3. Пусть универсальное множество U – множество всех сотрудников некоторой фирмы; A – множество всех сотрудников данной организации старше 35 лет; В – множество сотрудников, имеющих стаж работы более 10 лет; С – множество менеджеров фирмы. Определить содержательный смысл каждого из следующих множеств:
Практические задания к теме «Функции одной переменной» Пример 1.Найти область определения и множество значений функций
Решение. Областью определения функции y=sinx является множество всех вещественных чисел, а множество значений функции есть множество всех чисел, заключенных между –1 и 1, т.е. Х=(–¥; +¥) и Y=[–1; 1]. Так как функция Пример 2. Установить четность или нечетность функций
Решение. Область определения функции
Область определения функции
Для функции Практические задания к теме «Предел функции» Пример 1. Найти пределы Решение. 1) При х® –2 числитель и знаменатель дроби стремятся к нулю. Принято говорить, что получается неопределенность вида 0/0. Непосредственно теорему о пределе частного применить нельзя. Необходимо раскрыть эту неопределенность. Для этого разложим числитель и знаменатель на множители и сократим на общий множитель (х+2), который обращает в нуль числитель и знаменатель дроби. Получаем Неопределенность 0/0 раскрыта. Применяя теорему о пределе частного, имеем
2) Имеем неопределенность вида ¥/¥. Разделив на х числитель и знаменатель, получим 3) Имеем неопределенность вида 0/0. Разделив на (х-2) числитель и знаменатель, получим Пример 2.Найти предел Решение. Иногда при отыскании предела полезно произвести замену переменной с тем, чтобы упростить отыскание предела. Сделаем такую подстановку: kx=y. Отсюда следует, что при x®0 и y®0, a x=y/k. Тогда Пример 3. Найти Решение. 1) Сделаем замену переменной, полагая 1/x=a, тогда a®¥ при х®0, поэтому 2) Сделаем замену переменной, полагая х=kt, тогда t®¥ при x®¥. Следовательно, Практические задания к теме «Дифференциальное исчисление функции одной переменной» Пример 1. Найти производные функций: Решение. Полагая u=kx, имеем
Здесь Пример 2. Найти производные функций:
Решение.
Пример 3. Найти производные функций:
Решение.
Пример 4. Найти производные функций:
Решение.
Пример 5. Найти производные функций: Решение. В данных примерах целесообразно прибегнуть при нахождении производных к логарифмированию обеих частей равенств. Это желательно делать всегда, когда следует продифференцировать функцию вида
Пример 1. Найти Решение. Функция f(x) = х2 –1+lnx и g(x)= e x – e определены в окрестности точки х=1. Далее Предел отношения их производных существует
Пример 2. Найти Решение. Пример 3. Найти Решение. Здесь неопределенность вида Применяя правило Лопиталя, получим Пример 4. Найти Решение. Здесь неопределенность вида ¥ – ¥. Преобразуем разность
Неопределенности вида 00, 1¥, ¥0 сводятся к неопределенности вида Пример 5. Найти Решение. Имеем неопределенность вида 00. Но xх = e xlnx , и мы получили в показателе степени неопределенность вида
Практические задания к теме «Исследование функции» Пример 1. Исследовать функцию и построить ее график Решение. Функция определена на всей числовой прямой, кроме точки х=1. Так как В точке х=1 функция имеет разрыв II рода, т.к. Прямая х=1 является вертикальной асимптотой.
Найдем наклонные асимптоты.
Первая производная: Производная у¢(x) не существует при х=1 и у¢(х)=0 при х=0. Область определения разобьем критическими точками на интервалы (–¥; 0), (0; 1), (1; +¥) и определим знак у¢(х) в каждом из них: y¢(–1)=–1/4<0, y¢(1/2)=8>0, y¢(2)=–4<0. Таким образом, в интервалах первая производная имеет такую последовательность знаков: –, +, –. Приходим к заключению, что в критической точке х=0 имеет место минимум. Функция убывает на интервале (–¥; 0), возрастает на интервале (0; 1) и убывает на интервале (1; +¥); Вторая производная:
Производная у²(х) не существует в точке х=1 и равна нулю при х = ‑1/2. Область определения функции разобьем на интервалы (‑¥; ‑1/2), (–1/2; 1), (1;+¥) и определим знак у²(х) в каждом из них: у²(‑1)=–1/8<0, у²(0)=2>0, у²(2)=10>0. При переходе через критические точки II рода вторая производная меняет знак, следовательно, х = –1/2 – точка перегиба, у(–1/2)=–8/9. Функция выпукла на интервале (–¥; –1/2), вогнута на интервале (‑1/2; 1), вогнута на интервале (1; +¥). Если х=0, то у=–1; если у=0, то х=1/2. Следовательно, (0;1) и (1/2;0) — точки пересечения графика функции с осями системы координат. Результаты проведенного исследования сведем в таблицу:
Практические задания к теме «Неопределенный интеграл» Пример 1. Найти интеграл Пример 1. Найти интеграл Решение. Применив свойства о возможности вынесения из под знака интеграла постоянного множителя и о вычислении алгебраической суммы нескольких функций, стоящих под знаком интеграла, получим:
Используя соответствующие формулы таблицы основных интегралов, имеем:
Таким образом,
Обычно все произвольные постоянные суммируют, результат обозначают одной буквой
Пример 2. Найти интеграл Решение. Интеграл не табличный. Применим подстановку второго вида: t=3x, тогда dt=3dx, dx=dt/3. Подставляя в интеграл, имеем
Пример 3. Найти интеграл Решение. Применим подстановку первого вида
Чтобы перейти к переменной х, надо из подстановки Пример 4. Найти интегралы Решение. Положим
Положим
Практические задания к теме «Определенный интеграл» Пример 1. Вычислить интегралы
Практические задания к теме «Несобственные интегралы» Пример 1. Найти несобственный интеграл Решение. Это интеграл с бесконечным верхним пределом. Заменим верхний предел интегрирования на некоторую конечную величину b, устремив ее в пределе к бесконечности:
= Ответ: Пример 2. Найти несобственный интеграл Решение. Это несобственный интеграл с бесконечным нижним пределом. Заменим это предел на некоторую конечную величину a, устремив ее к бесконечности:
= Ответ: Пример 3. Найти несобственный интеграл Решение. Это несобственный интеграл с бесконечным верхним пределом. Заменим этот верхний предел на некоторую конечную величину b, устремив ее к бесконечности:
Выполним замену переменной под знаком интеграла
= Ответ: Пример 4. Найти несобственный интеграл Решение. Этот интеграл с бесконечным верхним пределом. Заменим верхний предел интегрирования на некоторую конечную величину b, устремив ее в пределе к бесконечности:
Ответ. Пример 1. В урне имеются 10 шаров: 3 белых и 7 черных. Из урны наугад вынимается один шар. Какова вероятность того, что этот шар: а) белый, б) черный? Решение. Пусть событие А состоит в том, что вынули белый шар, событие В состоит в том, вынули черный шар. Общее число исходов n=10 (шаров всего 10); число исходов, благоприятствующих событию А, m1=3 (можно вынуть 3 белых шара); число исходов, благоприятствующих событию В, m2=7 (можно вынуть 7 черных шаров). По классическому определению вероятности:
Ответ. Пример 2. Какова вероятность появления четного числа очков при одном бросании игрального кубика? (Игральный кубик – кубик, грани которого отмечены номерами 1, 2, 3, 4, 5, 6.) Решение. Пусть событие А состоит в том, что выпало четное число очков. Общее число исходов n=6. Число исходов, благоприятствующих событию А, m=3 (может выпасть 3 четных числа: 2, 4, 6).
Ответ. Пример 3. Брошены 3 монеты. Найти вероятность того, что выпадут два «герба». Решение. В результате подбрасывания каждой монеты возможно выпадение «герба» (обозначим такое событие Г) и выпадение «решки» (обозначим такое событие Р). Когда подбрасывают сразу 3 монеты, то возможны 8 различных исходов, которые можно объединить в пространство элементарных событий:
Пусть событие А состоит в том, что выпало ровно 2 «герба». Общее число исходов n=8. Число исходов, благоприятствующих событию А, m=3 (эти исходы подчеркнуты). Следовательно,
Ответ. Пример 4. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого случайным образом извлеченного жетона не содержит цифры 5. Решение. Событие А={номер жетона не содержит цифры 5}. Число всех исходов n=100. Для того чтобы подсчитать число исходов, благоприятствующих событию А, выпишем все номера, которые содержат цифру 5: 5, 15, 25, 35, 45, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 65, 75, 85, 95. Таких чисел 19, следовательно, m=100-19=81. Искомая вероятность:
Ответ. Практические задания к теме «Основные формулы комбинаторики» Пример 1. В урне 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: О, П, Р, С, Т. Найти вероятность того, что на вытянутых по одному и расположенных в одну линию кубиках можно будет прочесть слово «спорт». Решение. Событие А={слово «спорт»}. Комбинации, которые можно составить из 5 кубиков и которые будут различаться только порядком их расположения, – это перестановки. Число таких перестановок равно 5!=120. Следовательно, n=120, m=1 (так как из 120 составленных слов слово «спорт» получается 1 раз). Искомая вероятность
Ответ. Пример 2. В группе 30 студентов. Из них 12 юношей, остальные – девушки. Известно, что к доске должны быть вызваны двое студентов. Какова вероятность того, что это девушки? Решение. Событие А={к доске вызовут двух девушек}. Найдем число всех исходов испытания, состоящего в вызове двух студентов. Это число равно количеству способов, которыми можно выбрать двух студентов из 30. По условию задачи порядок вызова к доске не играет роли, поэтому
Ответ. Пример 3. Из пяти карточек с буквами А, Б, В, Г, Д наугад одна за другой выбираются три и располагаются в ряд в порядке появления. Какова вероятность, что получится слово «два». Решение. Событие А={слово «два»}. Найдем число всех исходов испытания, состоящего в выборе трех карточек. Это число равно количеству способов, которыми можно выбрать три карточки из пяти, порядок появления которых важен. Поэтому
Ответ. Пример 4. Опыт состоит в четырехкратном выборе с возвращением одной из букв множества {А, О, Б, К, М} и выкладывании слова в порядке поступления букв. Какова вероятность, что в результате будет выложено слово «мама». Решение. Число всех исходов будет равно
Практические задания к теме «Основные теоремы теории вероятностей» Пример 1. В денежно-вещевой лотерее на каждые 10000 билетов разыгрывается 150 вещевых и 50 денежных выигрышей. Чему равна вероятность выигрыша для владельца 1 лотерейного билета? Решение. Пусть событие А={вещевой выигрыш}, событие В={денежный выигрыш}, событие С={выигрыш}. Владелец одного лотерейного билета может выиграть вещевой или денежный выигрыш, следовательно, события А и В несовместны. Тогда С=А+В и
Ответ. 0,02. Пример 2. Вероятность поломки первого станка в течение смены равна 0,2, а второго – 0,13. Чему равна вероятность того, что оба станка потребуют наладки в течение смены? Решение. Пусть событие А={поломка первого станка}, событие В={поломка второго станка}, событие С={поломка обоих станков}. Тогда С=АВ. Так как события А и В независимы, то
Ответ. 0,026. Пример 3. Два спортсмена независимо друг от друга стреляют по одной мишени. Вероятность попадания в мишень первого спортсмена равна 0,7, а второго – 0,8. Какова вероятность того, что мишень будет поражена. Решение. |
|
 .
. .
. .
. ,
, .
. .
.

 ,
,  .
. .
.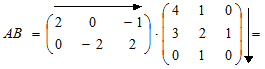

 , а матрица BA не существует.
, а матрица BA не существует. .
.
 :
:
 ,
, ,
, , так как первая строка пропорциональна второй.
, так как первая строка пропорциональна второй.


 .
. .
. .
. .
. .
. .
. .
.
 .
.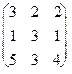 . Найти обратную матрицу.
. Найти обратную матрицу. .
.


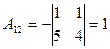





 .
. .
.
 ,
, .
. ~
~ 

 ~
~  .
. .
. .
. . Два минора третьего порядка, которые его окаймляют равны:
. Два минора третьего порядка, которые его окаймляют равны:  .
.




 ,
, .
.

 , где
, где  — присоединенная матрица к матрице A. Элементами присоединенной матрицы являются алгебраические дополнения элементов транспонированной матрицы A':
— присоединенная матрица к матрице A. Элементами присоединенной матрицы являются алгебраические дополнения элементов транспонированной матрицы A': .
.

 .
. .
. .
. .
.
 .
.
 ,
, ,
, ,
, .
. .
.
 .
.



 .
.
 }
} }
} ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  , A\B,
, A\B,  ,
, ,
,  .
. .
. представляет собой сумму функций, то область определения функции будет состоять из всех тех значений х, которые принадлежат одновременно области определения функций
представляет собой сумму функций, то область определения функции будет состоять из всех тех значений х, которые принадлежат одновременно области определения функций  . Поэтому область определения заданной функции определяется как совокупность значений х, при которых одновременно выполняются неравенства
. Поэтому область определения заданной функции определяется как совокупность значений х, при которых одновременно выполняются неравенства  и x–1>0. Это будет интервал (1; 2).
и x–1>0. Это будет интервал (1; 2). .
. (–¥; +¥);
(–¥; +¥); Следовательно, функция нечетная.
Следовательно, функция нечетная. [–1;1];
[–1;1]; следовательно, функция четная.
следовательно, функция четная.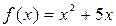 имеем
имеем  . Таким образом,
. Таким образом, 
 .
. .
. .
.
 .
. .
. .
. .
. .
.




 – производная косинуса,
– производная косинуса,  – производная корня,
– производная корня,  – производная дроби.
– производная дроби.









 ,
,  ,
,  ,
,  ,
, .
.

 ,
,
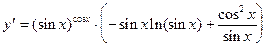 . Практические задания к теме «Правило Лопиталя для раскрытия неопределенностей»
. Практические задания к теме «Правило Лопиталя для раскрытия неопределенностей»
 , т.е. имеем неопределенность вида 0/0.
, т.е. имеем неопределенность вида 0/0. , причем g¢(x)¹0. Следовательно, эти функции удовлетворяют условиям правила Лопиталя, по которому предел
, причем g¢(x)¹0. Следовательно, эти функции удовлетворяют условиям правила Лопиталя, по которому предел  также существует и равен пределу отношения их производных
также существует и равен пределу отношения их производных .
.

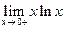 .
. . Преобразуем исходное выражение
. Преобразуем исходное выражение  , и мы получили неопределенность вида ¥/¥.
, и мы получили неопределенность вида ¥/¥. .
. .
. . Здесь неопределенность вида 0/0.
. Здесь неопределенность вида 0/0. .
. .
. .
. .
. и
и 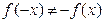 , то данная функция общего вида.
, то данная функция общего вида. , в остальных точках она непрерывна.
, в остальных точках она непрерывна. , следовательно, прямая у=0 — горизонтальная асимптота.
, следовательно, прямая у=0 — горизонтальная асимптота. ,
,  ,
, , что подтверждает отсутствие наклонной асимптоты при наличии горизонтальной.
, что подтверждает отсутствие наклонной асимптоты при наличии горизонтальной. .
. .
. .
.





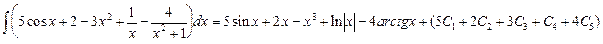
 . Окончательно получаем:
. Окончательно получаем: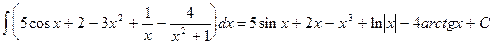 .
. .
. . Это табличный интеграл:
. Это табличный интеграл:  . Возвращаясь к переменной х, получим
. Возвращаясь к переменной х, получим .
. .
. и подынтегральная функция приобретает вид:
и подынтегральная функция приобретает вид: .
.
 найти
найти  , тогда
, тогда  .
. .
. тогда
тогда 

 , тогда
, тогда 
 .
. . Решение.
. Решение.


 , сделаем подстановку
, сделаем подстановку  , получим:
, получим:
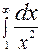 .
. =
=  =
=  =
=  =
=  =
= =
=  =
= 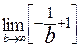 =
=  =1.
=1. .
. =
= 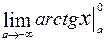 =
= = [ но arc tg 0 = 0, а arc tg
= [ но arc tg 0 = 0, а arc tg  = -
= -  ] =
] =  , несобственный интеграл сходится.
, несобственный интеграл сходится. .
. =
=  . [ z = ln x , dz =
. [ z = ln x , dz =  dx ]
dx ] =
=  =
=  =
= = [ но ln
= [ но ln  =
=  .
.
 , несобственный интеграл сходится. Практические задания к теме «Классическое определение вероятности»
, несобственный интеграл сходится. Практические задания к теме «Классическое определение вероятности» ,
,  .
. ;
;  .
. .
.
 .
.
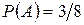 .
. .
. .
. .
. .
.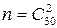 . Найдем теперь число благоприятствующих исходов. Для этого следует определить число способов выбора двух девушек из 18. Оно равно
. Найдем теперь число благоприятствующих исходов. Для этого следует определить число способов выбора двух девушек из 18. Оно равно  . По определению вероятности,
. По определению вероятности, .
. .
. . Найдем теперь число благоприятствующих исходов. Из 60 полученных слов слово «два» получится один раз
. Найдем теперь число благоприятствующих исходов. Из 60 полученных слов слово «два» получится один раз  . Искомая вероятность
. Искомая вероятность .
. .
. . Число благоприятствующих исходов равно m=1. Искомая вероятность
. Число благоприятствующих исходов равно m=1. Искомая вероятность .
. .
. .
.