|
|
Вплив речовини на поширення світла обумовлений взаємодією світла з атомами і молекулами, з яких складається речовинаЦя взаємодія призводить до зміни швидкості світла υ, а отже, визначає і значення показника заломлення п = Основи теорії дисперсії можуть бути одержані, якщо розглядати взаємодію світлових хвиль із зарядженими частинками (електронами і позитивними ядрами), що входять до складу атомів і молекул. При цьому передбачається, що заряджені частинки в атомах і молекулах утримуються біля своїх положень рівноваги квазіпружними силами. Таким чином, кожен атом або молекула мають певну власну частоту коливань w0. Під впливом падаючої світлової хвилі заряджені частинки в атомах і молекулах здійснюють вимушені коливання з частотою, співпадаючою з частотою падаючої хвилі w. Первинна електромагнітна (світлова) хвиля, поширюючись через речовину зі швидкістю с, викликає вимушені коливання частинок. Завдяки цьому біля кожної частинки виникнуть вторинні хвилі. Амплітуда і фаза цих вторинних хвиль визначаються амплітудою і фазою вимушених коливань частинок; останні ж залежать від співвідношення між частотою падаючої хвилі w і частотою власних коливань w0. Таким чином, у речовині поширюються хвиля первинна і вторинна. Фаза вторинних коливань запізнюється відносно первинних, і тому виникає деяка різниця фаз. (Запізнення відбувається внаслідок того, що самі ці заряджені молекули мають деяку інерцію). Швидкість сумарної хвилі менша за швидкість первинної хвилі, тобто має місце показник заломлення. При вивченні гармонійних коливань ми встановили, що періодична вимушуючи сила з частотою w викликає вимушене коливання з амплітудою
і фазою α, яка визначається рівністю:
Тут h — константа, β – коефіцієнт, що характеризує загасання коливань системи. При малому значенні коефіцієнта β, роль загасання помітна лише для частот вимушуючої сили w, які близькі до частот власних коливань w0. Тому при слабкому загасанні для всіх частот w, не дуже близьких до w0, можна приблизно написати:
Амплітуда і фаза вимушених коливань залежать від співвідношення частот w0 і w. Поблизу резонансу амплітуда А велика. При w<<w0 амплітуда А значно менше і із зменшенням w прямує до постійної границі, не рівної нулеві. Якщо Вторинні хвилі, складаючись із первинною, утворюють результуючу хвилю з амплітудою і фазою, відмінними від амплітуди і фази первинних хвиль. Це призводить до того, що хвиля проходить через речовину з фазовою швидкістю, відмінною від швидкості, з якою вона розповсюджувалася б у порожнечі. Відмінність у швидкостях буде тим більша, чим сильніші вимушені коливання частинок. Звідси витікає, що світло (електромагнітні хвилі), частота якого набагато менше частот власних коливань атомів або молекул, проходить через речовину з швидкістю, практично не залежною від частоти, але відмінною від швидкості світла у вакуумі (оскільки А ≈ const ≠ 0). Для світла дуже великої частоти, що помітно перевищує частоти власних коливань атомів, амплітуда вторинних хвиль близька до нуля, він проходить через речовину з швидкістю, близькою до швидкості світла у вакуумі. Показник заломлення для таких речовин близький до одиниці. В обох розглянутих випадках, як випливає з теорії, поглинання світла незначне. При значеннях частот, w близьких до w0, швидкість світла в речовині починає дуже відрізнятися від його швидкості у вакуумі. Завдяки цьому і показник заломлення дуже відрізняється при цих частотах від одиниці: при w<w0 він виявляється «аномально» великим; при w>w0 — «аномально» малим. Крім того, при w близькому до w0, в результаті великих амплітуд вимушених коливань велике і поглинання. Речовина, що складається з атомів або молекул із певним набором частот власних коливань w0і, дасть у спектрі вузькі лінії (лінії поглинання). Показник заломлення виявиться постійним в областях, далеких від поглинання, і швидко мінятиметься з частотою і дуже відрізнятиметься від одиниці поблизу кожної лінії поглинання, де взаємодія світла з речовиною велика. ІІ. За електромагнітною теорією світла показник заломлення визначається рівністю
Для всіх прозорих діелектриків магнітна проникність μпрактично рівна одиниці, тому маємо:
Діелектричні властивості речовини обумовлені її поляризацією, яка виникає у зв’язку зі зміщенням заряджених часток у атомі або молекулі, відносно положення рівноваги внаслідок дії електромагнітних хвиль. При цьому значення діелектричної постійної ε не буде бути постійним. Для швидко змінних електричних полів, які мають місце в світловій хвилі, ці зміни виражаються знайденою нами амплітудою. Тому, як показує теорія, квадрат коефіцієнта заломлення n2 виражається наступною дисперсійною формулою:
де w01, w02, … — частоти власних коливань атомів або молекул, а1, а2…— деякі константи. Оскільки довжина хвилі λ пов’язана з циклічною частотою співвідношенням:
де с — швидкість світла у вакуумі, то формулі (4.22) можна також надати вигляду:
де b1, b2 ... – нові константи, а λ1, λ2, ... – довжини хвиль, відповідні резонансу. Формула (4.24) дає значення показника заломлення в проміжку між лініями поглинання. Якщо обмежитися у формулі (4.24) двома членами (речовина з двома власними частотами коливань), то вийде залежність п2–1від λ,зображена
Рис. 4.36. Залежність коефіцієнта заломлення n від довжини хвилі λ поблизу двох ліній поглинання λ1 і λ2
на рисунку 4.36. Пунктирні лінії показують положення ліній поглинання речовини λ1 і λ2. Поблизу ліній поглинання крива дисперсії круто згинається. У кожної лінії поглинання з боку малих довжин хвиль (λ < λі) коефіцієнт заломлення n приймаємалі значення, а з боку великих довжин хвиль (λ > λі) — вельми великі значення. За формулою (4.24) для довжини хвилі, меншої і дуже близької до однієї з λ,для п2 вийдуть від’ємні значення, що дає уявні значення для n. Це відбувається через те, що не врахований коефіцієнт загасання β. Тому формулою (4.24) можна користуватися лише в областях, де β дуже мале. Далеко від ліній поглинання значення показника заломлення п наближаєтьсядо постійних величин. Загальний хід дисперсії, зображений на рисунку, з характерними вигинами біля ліній поглинання має назву «аномальної» дисперсії. Насправді в цьому ході немає нічого «аномального», навпаки, він є типовим ходом, що відповідає фізичній суті явища. Область монотонної зміни показника заломлення між двома лініями поглинання передає характер дисперсії прозорих речовин і має назву нормальної дисперсії. Спостереження дисперсії Першими дослідами зі спостереження дисперсії були описані досліди Ньютона із заломлення світла у призмі. Ньютон розробив ряд методів спостережень дисперсії за допомогою призм і зокрема метод схрещених призм, що досить точно виявляє хід дисперсії. Схема методу схрещених призм дана на рисунку 4.37.
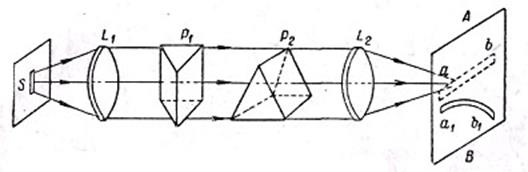
Рис.4.37. Метод схрещених призм
Біле світло проходить через вертикальну щілину S і дві призми P1 і Р2, заломлюючі ребра яких взаємно перпендикулярні. За допомогою лінз L1і L2світло збирається на екрані АВ. За наявності тільки однієї призми P1з вертикальним заломлюючим ребром, на екрані АВ вийшов би горизонтальний суцільний спектр, зображений пунктирною смужкою ab. За наявності другої призми кожен промінь буде відхилений униз тим сильніше, чим більше для нього коефіцієнт заломлення призми Р2. Завдяки цьому весь спектр ab виявиться зміщеним вниз і займе положення a1b1. Його червоний кінець а1зміщений униз менше всього, а фіолетовий кінець b1 – найбільше. Також і кожне інше місце спектру зміститься тим більше, чим більше коефіцієнт заломлення для довжини хвилі, відповідної цьому місцю спектру. Вся смужка a1b1буде зігнута і наочно представить хід дисперсії в призмі Р2. Дисперсія скла, кварцу, флюориту і багатьох інших речовин у видимій частині спектру визначається головним чином наявністю сильних ліній поглинання в ультрафіолетовій області. Друга область поглинання у цих речовин лежить у дальній інфрачервоній частині і позначається менше. Приблизно для видимої частини спектру залежність п2 від λ для цих речовин може бути представлена дисперсійною формулою з одним членом:
Розкладаючи праву частину цієї формули в ряд, одержимо:
Тобто приблизно для п:
де А, В, С—деякіконстанти. Аномальна дисперсія найлегше спостерігається в парах металів, що дають у видимій частині спектру різкі лінії поглинання. Так, пари натрію дають у жовтій частині дві вельми інтенсивні близькі лінії поглинання з довжинами хвиль λ1= 0,5890 МК та λ2 = 0,5896 МК. Р.Вуд використовував для спостереження «аномальної» дисперсії в парах натрію метод схрещених призм. Схема його досліду представлена на рисунку 4.38. Світло від джерела суцільного спектру проходить через горизонтальну щілину S1 і потім у вигляді паралельного пучка — через посудину АВ,що містить металевий натрій. Пройшовши через посудину, світло падає на вертикальну щілину S2і розкладається призмою Р2 в спектр.
Рис.4.38
Заломлююче ребро призми Р2 паралельне щілині S2, і спектр виходить у вигляді горизонтальної смужки. Завдяки наявності горизонтальної щілини S1 ця смужка вузька. Якщо підігріти металевий натрій у посудині АВ знизу і одночасно охолодити верхню частину посудини АВ, то в ній виникне неоднорідний стовп пари натрію. Внизу щільність пари буде більша, вгорі менше. Такий неоднорідний стовп пари діє як призма із заломлюючим ребром, розташованим зверху, перпендикулярно до довжини посудини. В результаті вийде «призма» з пари натрію, схрещена з призмою Р2. Ця призма, як було пояснено вище, змістить всі частини спектру.
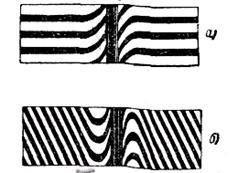
Рис. 4.39. Аномальна дисперсія в парах натрію, поблизу ліній поглинання: а) при малій густині; б) при великій густині парів натрію.
Проте тепер, завдяки аномальному характеру дисперсії пари натрію, зміщений спектр буде не монотонно зігнутим, а виявить характерні вигини поблизу довжин хвиль λ1 і λ2. У місцях, хвиль λ1 і λ2, що відповідають цим довжинам, з'являться темні лінії поглинання. На рисунку 4.39а представлений одержуваний вигин спектру. В бік великих довжин хвиль від ліній поглинання спектр сильно відхилений вниз, що відповідає великим значенням показника заломлення натрію в цій області. В бік коротких довжин хвиль від ліній поглинання спектр зігнутий вгору, що указує на значення показника п<1. Між обома лініями поглинання показник заломлення круто спадає у разі збільшення довжин хвиль. При великій щільності пари вигин спектру збільшується і приймає вигляд, зображений на рисунку 4.39б. Інший метод вивчення аномальної дисперсії запропонований Д.С.Рож-дественським.
Д. С. Рождественський використовував свій інтерферометр для вивчення аномальної дисперсії. Суть методу полягає в наступному. В обидві гілки інтерферометра вводяться дві однакові кювети В1 і В2 (рис. 4.41). В одну з кювет, наприклад В2, вводиться досліджуваний метал; ця кювета може нагріватися електричною піччю до температури, достатньої для того, щоб в ній створити пари металу при необхідному тиску. Друга кювета відкачується. Через інтерферометр пропускається світло від джерела суцільного спектру S. Виникаюча інтерференційна картина проектується за допомогою лінзи L2 на щілину спектрографа С. Припустимо, що спочатку кювета В2 не нагріта, і в ній відсутні пари. Тоді інтерферометр дасть на щілині спектрографа ряд інтерференційних максимумів і мінімумів у вигляді ліній, перпендикулярних до довжини щілини. Положення максимуму, відповідного нульовій різниці ходу, не залежить від довжини хвилі. Звідси витікає, що цьому максимуму в суцільному спектрі, що дає спектрограф, відповідає горизонтальна світла лінія, що тягнеться уздовж всього спектру. Максимуми ж, що відповідають різницям ходу в одну, дві, три і т.д. довжини хвилі, розташовуються для різних довжин хвиль падаючого світла на різних висотах щілини. Їм відповідають у суцільному спектрі світлі лінії, розташовані вище і нижче за нульову лінію, що розходяться віялом від синьої частини спектру до червоної. Між світлими лініями розташовуються темні, що відповідають мінімумам в інтерференційній картині, відкинутій на щілину. В результаті суцільний спектр виявляється уздовж всієї довжини прокресленим поперемінно світлими і темними лініями. Якщо тепер нагрівати кювету В2 рис.4.41 настільки, щоб у ній з'явилися пари досліджуваного металу, то стовп цієї пари дасть додаткову різницю ходу, і інтерференційні лінії змістяться на величину, пропорційну цій додатковій різниці ходу. Різниця ж ходу при даній довжині стовпа пари пропорційна n-1, де n – показник заломлення пари.
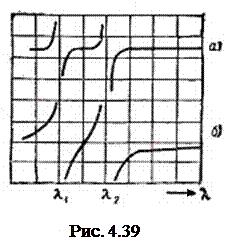
Рис. 4.41 Завдяки цьому зсув інтерференційних ліній у спектрографі безпосередньо відтворить хід дисперсії в усій спостережуваній області. Якщо на цю область припадає яка-небудь з ліній поглинання досліджуваної пари, то інтерференційні лінії зігнуться біля неї. Їх вигин наочно зобразить зміну показника заломлення поблизу лінії поглинання (рис. 4.42а).
Рис. 4.42 Згодом Д.С.Рождественський удосконалив указаний метод, що дозволило проводити точні кількісні виміри. Він показав, що якщо в другу гілку інтерферометра ввести плоско-паралельну пластинку зі скла, то інтерференційні лінії в спектрографі перегнуться і утворять поблизу лінії поглинання своєрідні "крюки" (рис. 4.42б). При даній товщині скляної пластинки положення "крюків" визначиться величиною дисперсії біля даної лінії поглинання пари. Чим сильніше дисперсія пари поблизу лінії, тим далі від лінії утворюються "крюки". Таким чином, за положенням "крюків" можна безпосередньо виміряти величину дисперсії пари біля лінії поглинання. |
|
 , де с – швидкість світла у вакуумі.
, де с – швидкість світла у вакуумі. 4.19
4.19 4.20
4.20 4.21
4.21 . Ті ж висновки відносяться до амплітуди і фази вторинних хвиль.
. Ті ж висновки відносяться до амплітуди і фази вторинних хвиль. .
. .
. 4.22
4.22 , 4.23
, 4.23 4.24
4.24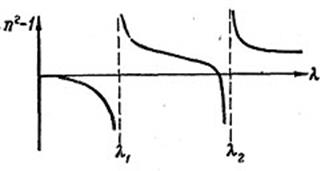
 4.25
4.25 4.26
4.26 4.27
4.27
 Д.С.Рождественський видозмінив інтерферон-метр Жамена таким чином, що пучки 1 і 2 можуть бути розведені один від одного на багато сантиметрів. Схема інтерферометра Рождественсь-кого зображена на рисунку 4.40, де А1 A2, A3, А4 — чотири плоскі дзеркала, з яких дзеркала A2 та A3 суцільні, а інші два — напівпрозорі. При відбиваннях від дзеркал А1 і А2 виникають сильно розведені пучки світла 1 і 2, які потім знову збираються разом за допомогою дзеркал А3 і A4 і інтерферують.
Д.С.Рождественський видозмінив інтерферон-метр Жамена таким чином, що пучки 1 і 2 можуть бути розведені один від одного на багато сантиметрів. Схема інтерферометра Рождественсь-кого зображена на рисунку 4.40, де А1 A2, A3, А4 — чотири плоскі дзеркала, з яких дзеркала A2 та A3 суцільні, а інші два — напівпрозорі. При відбиваннях від дзеркал А1 і А2 виникають сильно розведені пучки світла 1 і 2, які потім знову збираються разом за допомогою дзеркал А3 і A4 і інтерферують.