|
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮМАТЕМАТИКА (ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА) Методические указания к изучению дисциплины и выполнению контрольной работы № 3 для студентов заочной формы обучения
Специальности: 080105 - Финансы и кредит 080109 - Бухгалтерский учет, анализ и аудит 080111 - Маркетинг 080502 - Экономика и управление на предприятии (по отраслям) 080504 - Государственное и муниципальное управление 080506 - Логистика 080507 - Менеджмент организации 220501 – Управление качеством
Санкт-Петербург Допущено редакционно-издательским советом СПбГИЭУ в качестве методического издания
Составители:
ст. преп. В. Г. Блинова канд. техн. наук, доцент Я. В. Войтишек ст. преп. Е. Н. Зверева
Рецензент канд. хим. наук, доцент В.В. Фокин
Подготовлено на кафедре высшей математики
Одобрено научно-методическим советом университета
Отпечатано в авторской редакции с оригинал-макета, представленного составителями © СПбГИЭУ, 2006 Содержание 1. Общие положения……………………………………………...4 2. Методические указания к изучению дисциплины.…………..4 3. Методические указания к выполнению заданий № 1- № 4 Комментарии к задаче № 1 §1. Случайные события. Основные понятия…………………….5 §2. Случайные события. Операции………………………………6 §3. Классическое определение вероятности……………………..6 §4. Примеры задач на классическую вероятностную схему……8 §5. О статистической и геометрической вероятностях…………9 §6. Простейшие свойства вероятностей………………………..10 §7. Условные вероятности. Независимость событий………….11 §8. Вероятность наступления хотя бы одного события……….12 §9. Формула полной вероятности………………………………14 §10. Формула Байеса……………………………………………..16 Комментарии к задаче № 2 §11. Повторные независимые испытания………………………17 §12. Другие формулы вычисления вероятностей для схемы Бернулли…………………………………………………………..19 Комментарии к задаче № 3 §13. Случайные величины дискретного типа…………………..22 §14. Функция распределения…………………………………….23 §15. Математическое ожидание случайной величины дискретного типа…………………………………………………24 §16. Дисперсия случайной величины…………………………..26 §17. Биномиальный и пуассоновский законы распределения…26 Комментарии к задаче № 4 §18. Случайные величины непрерывного типа…………………28 §19. Нормальный закон распределения и его характеристики……………………………………………………30 §20. Другие законы распределения непрерывных случайных величин……………………………………………………………31 4. Методические указания к выполнению задания № 5……….32 5. Контрольные задания № 1- № 4.……………………………...53 6. Контрольные задания № 5.……………………………………71 7. Выбор варианта. Требования к оформлению контрольной работы.…………………………………………..79 8. Список литературы……………………………………….…...80 Приложение 1 Таблица случайных чисел…………….………...81 Приложение 2 Нормированная функция Лапласа.………….………83 Приложение 3 Значения чисел q в зависимости от объёма выборки n и надёжности Приложение 4 Критические точки распределения Приложение 5 Содержание дисциплины..……………………..87 Приложение 6 Образец оформления титульного листа контрольной работы.…………………………………………….90 Приложение 7 Перечень контрольных вопросов для проверки знаний по дисциплине.……………………………….91 ОБЩИЕ ПОЛОЖЕНИЯ Цель дисциплины «Математика (Теория вероятностей и математическая статистика)» - дать необходимый математический аппарат и привить навыки его использования при решении инженерно-экономических задач. Для этого при изучении курса студенты осваивают методы математического моделирования экономических и иных возникающих на практике ситуаций, вероятностные методы их исследования и решения, методы обработки статистических данных (аналитически и при помощи вычислительной техники), а также методы дальнейшего анализа полученных результатов. Это способствует также развитию логического и алгоритмического мышления. Теория вероятностей опирается на предшествующие разделы математики, как на курс средней школы, так и на разделы, изучавшиеся на 1 курсе (множества, функции, непрерывность, производные, интегралы, ряды). Студенты 2 курса, имеющие зачтенные контрольные работы № 3 и № 4, допускаются к экзамену по математике.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИЗУЧЕНИЮ ДИСЦИПЛИНЫ Изучение дисциплины следует начать с теоретической части данных методических указаний. Поскольку методические указания не являются учебником и теоретический материал здесь изложен кратко, полезно обратиться к учебникам, перечисленным в списке литературы. Для изучения дисциплины в общепринятом логическом порядке полезно сверяться с Приложением 5 данного издания. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЙ № 1 - № 4 КОММЕНТАРИИ К ЗАДАЧЕ № 1
СЛУЧАЙНЫЕ СОБЫТИЯ. ОСНОВНЫЕ ПОНЯТИЯ
Случайным называется событие, которое при осуществлении совокупности некоторых условий S может либо произойти, либо не произойти. Пример: событие А1 - выпадение “шестерки” при одном броске игральной кости (кубика с занумерованными гранями). Достоверным называют событие, которое обязательно произойдет, если будет осуществлена совокупность условий S. Пример: событие А2 - при одном броске игральной кости число выпавших очков меньше 7. Обозначим достоверное событие буквой W. Невозможным называют событие, которое заведомо не произойдет при осуществлении совокупности событий S. Пример: событие А3 - при одном броске игральной кости число выпавших очков дробно. Невозможное событие обозначим символом Æ. События W и Æ будем рассматривать как частные (“крайние”) случаи случайных событий, хотя они не являются таковыми. Два или более событий назовем несовместными, если в результате осуществления условий S (или, по-другому, в результате испытания) невозможно их совместное осуществление, т.е. появление одного из них исключает появление другого в том же испытании. Пример: событие А4 - при броске игральной кости выпало нечетное число очков - несовместно с событием А1 (выпала “шестерка”).
§2. СЛУЧАЙНЫЕ СОБЫТИЯ. ОПЕРАЦИИ
Сумма событий А + В - событие, состоящее в том, что произошло хотя бы одно из двух событий А и В, т.е. наступило либо А, либо В, либо оба сразу. Пример: для событий А1 и А4 из §1 А1 + А4 = {выпало 1,3,5 или 6 очков}. Произведение событий А · В - это совместное осуществление и А и В (иначе: их общие исходы). Пусть В = {при броске игральной кости выпало число очков, кратное 3}. Тогда В · А4 = {выпала грань с 3 очками}. Для несовместных событий А и В их произведение А·В=Æ : у них нет общих исходов. В частности, для последнего примера §1 можно записать А1 ·А4 = Æ. Событие Для операций над событиями выполняются свойства:
Если события Н1, Н2, ..., Нn попарно несовместны (Нi·Hj=Æ при i ¹ j ), а их сумма - достоверное событие (H1+H2+...+Hn = W ), то говорят, что {H1, H2, ..., Hn} - полная группа несовместных событий или разбиение W. В частности, {A,
§3. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
Вероятность события А - это число Р(А), которое вводится для количественного описания степени объективной возможности наступления А. В этом параграфе рассмотрим испытания, в которых множество W представляет собой конечное число равновозможных исходов. Например, если бросить игральную кость один раз, то она может выпасть на любую из шести граней. Достоверное событие W здесь состоит в том, что выпала одна из шести граней. Будем считать кубик симметричным; в этом случае можно считать все шесть исходов равновозможными. В случае двух бросков симметричной монеты - 4 различных исхода: “орел-орел” (О, О), “орел-решка”(О, Р), а также Р, О и Р, Р; их также считают равновозможными. Все они вместе образуют достоверное событие W для данного испытания. В первом случае вероятность каждого из элементарных исходов равна 1/6, а во втором 1/4. В общем случае, если число всех элементарных исходов N(W) равно n, то вероятность каждого из них 1/n. Пусть число благоприятствующих исходов для А или, иначе, число элементарных исходов испытания, входящих в событие А ( N(A) ), равно m, тогда вероятность
Это формула классической вероятности. В примерах из §1 шесть элементарных исходов: выпала цифра 1, 2, 3, 4, 5 или 6. Событие А1 включает в себя ровно 1 элементарный исход, А2 (достоверное) - все 6, А3 (невозможное) - 0, А4 - 3. Поэтому
Еще примеры. При двух бросках симметричной монеты событие С = {выпал хотя бы один “орел”} включает в себя три элементарных исхода из четырех, поэтому Событию D = {при трех бросках монеты выпало ровно два ”орла”} благоприятствуют 3 из 8 возможных элементарных исходов, поэтому
|
|
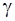 для определения доверительного интервала среднего квадратического отклонения
для определения доверительного интервала среднего квадратического отклонения 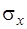 .….……..85
.….……..85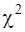 ...………86
...………86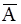 называется противоположным к А (т.е. состоит в том, что “ достоверное событие W происходит, а событие А не происходит”).
называется противоположным к А (т.е. состоит в том, что “ достоверное событие W происходит, а событие А не происходит”).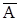 } - полная группа несовместных событий для любого А.
} - полная группа несовместных событий для любого А.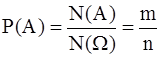 ( 1 )
( 1 )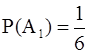 ,
, 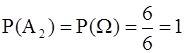 ,
,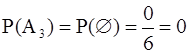 ,
, 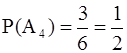
 .
.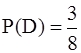 .
.