|
|
Интервальный вариационный ряд
2) После составления вариационного ряда необходимо построить функцию распределения выборки или эмпирическую функцию F*(x)= Эмпирическое распределение можно изобразить в виде полигона, гистограммы или ступенчатой кривой.
Таблица 6 Расчёт эмпирической функции распределения
Табличные значения не полностью определяют выборочную функцию распределения непрерывной случайной величины, поэтому при графическом изображении её доопределяют, соединив точки графика, соответствующие концам интервала, отрезками прямой (рис.1). Полученные данные, представленные в виде вариационного ряда, изобразим графически в виде ломаной линии (полигона), связывающей на плоскости точки с координатами Таблица 7 Дискретный вариационный ряд
Рис.1
Рис.2
На основании полученных выборочных данных необходимо сделать предположение, что изучаемая величина распределена по некоторому определённому закону. Для того чтобы проверить, согласуется ли это предположение с данными наблюдений, вычисляют частоты полученных в наблюдениях значений, т.е. находят теоретически сколько раз величина Х должна была принять каждое из наблюдавшихся значений, если она распределена по предполагаемому закону. Для этого находят выравнивающие (теоретические) частоты по формуле:
где n – число испытаний,
Эмпирические (полученные из таблицы) и выравнивающие частоты сравнивают, и при небольшом расхождении данных делают заключение о выбранном законе распределения. Предположим, что случайная величина Х распределена нормально (см. комментарии к задаче № 4). В этом случае выравнивающие частоты находят по формуле:
где n-число испытаний, h-длина частичного интервала,
Результаты вычислений отобразим в таблице №8. Сравнение графиков (рис.2) наглядно показывает близость выравнивающих частот к наблюдавшимся и подтверждает правильность допущения о том, что обследуемый признак распределён нормально.
Таблица 8 Расчёт выравнивающих частот
Интервальный вариационный ряд графически изобразим в виде гистограммы (рис.3). На оси Х отложим интервалы длиной h=3, а на оси Y значения Графическое изображение вариационных рядов в виде полигона и гистограммы позволяет получать первоначальное представление о закономерностях, имеющих место в совокупности наблюдений.
3) Найдём числовые характеристики вариационного ряда, используя таблицу №4. Выборочная средняя (
или где а В некоторых случаях
где С – произвольно выбранное число (ложный нуль). В этом случае
Для изменения значения варианты можно ввести также условные варианты путём использования масштабного множителя:
где
Выборочная дисперсия (
Среднеквадратическое отклонение:
Найдем несмещённую оценку дисперсии и среднеквадратического отклонения («исправленную» выборочную дисперсию и среднеквадратическое отклонение) по формулам:
Доверительный интервал для оценки математического ожидания с надёжностью P( Из соотношения Ф(z)= 168,55-1,96 167,67<a<169,43. Доверительный интервал для оценки среднего квадратичного отклонения случайной величины находят по формуле:
где S – несмещённое значение выборочного среднего квадратичного отклонения; q – параметр, который находится по таблице (Приложение В) на основе известного объёма выборки n и заданной надёжности оценки На основании данных значений
5,79< V= 4) Проведём статистическую проверку гипотезы о нормальном распределении. Нормальный закон распределения имеет два параметра (r=2): математическое ожидание и среднее квадратическое отклонение. По выборочным данным (таблицы 5 и 7) полученные оценки параметров нормального распределения, вычисленные выше:
Для расчёта теоретических частот - по нормированным значениям случайной величины Z находят значения Ф(z), а затем
Например,
- далее вычисляют вероятности - находят числа Результаты вычисления По формуле
можно сделать проверку расчетов.
По таблице (приложения Г) можно найти число При α=0,1 При α=0,01 Таблица 9 Определение
2 часть 1) Данные таблицы 3 сгруппируем в корреляционную таблицу 10. 2) Строим в системе координат множество, состоящее из 200 экспериментальных точек (рисунок 4). По расположению точек делаем заключение о том, что экономико-математическую модель можно искать в виде 3) Найдём выборочные уравнения линейной регрессии. Для упрощения расчётов разобьём случайные величины на интервалы и выберем средние значения. Для величины Х указанные действия были выполнены в 1 части задания. Таблица 10 Корреляционная таблица
Рис.4 Для случайной величины Y, используя (1), получим h=2, число интервалов равно 13. Результаты внесём в таблицу со сгруппированными данными №11. Находим средние значения
Используя формулы:
получим
Таблица 11 Сгруппированные данные выборки
4) Вычисляем выборочный коэффициент корреляции
Принято считать, что если 0,1< Для данного примера связь между X и Y умеренная. Затем получают выборочное уравнение линейной регрессии Y на X в виде:
и выборочное уравнение линейной регрессии X на Y :
Вычисления сумм рекомендуем проводить с помощью пакетов прикладных математических программ (сегодня их существует много).
КОНТРОЛЬНЫЕ ЗАДАНИЯ № 1-№ 4 Вариант 1. 1. Фирма имеет три источника поставки комплектующих – фирмы А, В и С. На долю фирмы А приходится 50% общего объема поставок, В – 30% и С – 20%. Из практики известно, что 10% поставляемых фирмой А деталей бракованные, фирмой В – 5% и фирмой С – 6%. 1) Какова вероятность, что взятая наугад деталь была получена от фирмы А? 2) Какова вероятность, что взятая наугад и оказавшаяся бракованной деталь получена от фирмы А? 2. Накануне выборов 40% населения поддерживают «Партию квадратов», 40% - «Партию Кругов» и 20% еще не определились во мнении. Какова вероятность того, что, по крайней мере, половина из шести наудачу выбранных избирателей оказывают доверие «Партии квадратов»? 3. Имеется 8 изделий, из которых 3 дефектных. Для контроля взято наудачу 3 изделия. Случайная величина Х – число дефектных изделий в выборке. 1) Составить таблицу распределения Х. 2) Найти математическое ожидание M(X) и дисперсию D(Х). 3) Построить график функции распределения y = F(x) 4) Найти вероятность P(0,5<X<3). 4. Фирма «Клубок ниток» производит вязальные спицы. Наиболее популярны размеры
«Клубок» производит нарезку игл из проволоки и их дальнейшую обработку. В результате чего средний диаметр заготовок становится 3.10 мм, а его среднее квадратическое отклонение 0.10 мм. Допустим, значение диаметра подчиняется закону нормального распределения. Требуется определить долю заготовок, пригодных для производства спиц №11, учитывая, что дальнейшая обработка не изменяет диаметр заготовок.
Вариант 2. 1. В центральную бухгалтерию корпорации поступили пачки накладных для проверки и обработки. 90% пачек были признаны удовлетворительными: они содержали только 1% неправильно оформленных накладных. Остальные 10% пачек накладных были признаны неудовлетворительными, так как содержали 5% неправильно оформленных накладных. Взятая наугад из пачки накладная оказалась оформленной неправильно. Учитывая это, какова вероятность того, что вся пачка накладных будет признана не соответствующей стандартам? |
|



 =1
=1 , то есть функцию найденную опытным путём. Здесь
, то есть функцию найденную опытным путём. Здесь  – относительная частота события Х< х, n - общее число значений.
– относительная частота события Х< х, n - общее число значений. Построим выборочную функцию распределения. Очевидно, что для
Построим выборочную функцию распределения. Очевидно, что для  функция
функция  так как
так как  . На концах интервалов значения функции
. На концах интервалов значения функции  рассчитаем в виде «нарастающей относительной частоты» (Таблица 6).
рассчитаем в виде «нарастающей относительной частоты» (Таблица 6). , где
, где 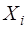 - среднее значение интервала
- среднее значение интервала  , а
, а  - относительная частота.(таблица 7 и рис.2). На этом же рисунке отобразим пунктирной линией выравнивающие (теоретические) частоты.
- относительная частота.(таблица 7 и рис.2). На этом же рисунке отобразим пунктирной линией выравнивающие (теоретические) частоты.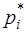



 (7)
(7)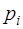 - вероятность наблюдаемого значения
- вероятность наблюдаемого значения  , вычисленная при допущении, что Х имеет предполагаемое распределение.
, вычисленная при допущении, что Х имеет предполагаемое распределение. (8)
(8) -выборочное среднее квадратичное отклонение,
-выборочное среднее квадратичное отклонение, (
(  – функция Лапласа (9)
– функция Лапласа (9)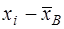






 ):
):
 , (10)
, (10) - частоты,
- частоты, -объём выборки. Выборочная средняя является оценкой математического ожидания (среднего значения теоретического закона распределения).
-объём выборки. Выборочная средняя является оценкой математического ожидания (среднего значения теоретического закона распределения). (11)
(11) . (12)
. (12)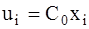 , (13)
, (13) (b выбирается положительным или отрицательным числом).
(b выбирается положительным или отрицательным числом).
 . Здесь С – середина 8-го интервала.
. Здесь С – середина 8-го интервала.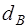 ):
): (14)
(14) (15)
(15) =
=  (1*441+0*324+…+1*324)- 1,95²=40,21
(1*441+0*324+…+1*324)- 1,95²=40,21 =
=  (16)
(16) =
=  =6,34
=6,34 и
и  (17)
(17) =
=  =40,41 и S=
=40,41 и S=  6,34=6,36
6,34=6,36 0,95 определяют по формуле:
0,95 определяют по формуле: -t
-t  Ф(t)=
Ф(t)= 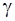 (18)
(18) ,
, , (19)
, (19) ,
,
 (20)
(20)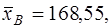
 ,
,  , S=6,36.
, S=6,36. используют табличные значения функции Лапласа Ф(z). Алгоритм вычисления
используют табличные значения функции Лапласа Ф(z). Алгоритм вычисления  :
: ,
,  =0,5+Ф(
=0,5+Ф(  ).
). ;
;  ; Ф(-3,0)=-0,4987;
; Ф(-3,0)=-0,4987; ;
; ;
; , и если некоторое
, и если некоторое  <5, то соответствующие группы объединяются с соседними.
<5, то соответствующие группы объединяются с соседними. приведены в таблице 9.
приведены в таблице 9. (21)
(21)
 по схеме: для уровня значимости α=0,05 и числа степеней свободы l=k-r-1=9-2-1=6
по схеме: для уровня значимости α=0,05 и числа степеней свободы l=k-r-1=9-2-1=6 
 ). Величина
). Величина  =15,61 входит в критическую область, поэтому гипотеза о том, что случайная величина Х подчинена нормальному закону распределения, отвергается.
=15,61 входит в критическую область, поэтому гипотеза о том, что случайная величина Х подчинена нормальному закону распределения, отвергается.
 )
)








 149,5
149,5

 ,0000
,0000 
 .
.


 , по формулам:
, по формулам: , (22)
, (22) , (23)
, (23) , (24)
, (24) . (25)
. (25)


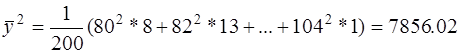
 149,5*86+155,5(82+…+90)+…+188,5*104=2986101
149,5*86+155,5(82+…+90)+…+188,5*104=2986101 , (26)
, (26) , (27)
, (27) =
=  ,
,  =
= 
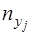

 по формуле:
по формуле: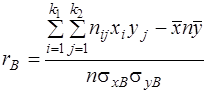 . (28)
. (28)
 (29)
(29) . (30)
. (30) и
и
 или
или