|
|
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ ДИСКРЕТНОГО ТИПА.
Cлучайной величиной называют величину, которая в результате испытания примет одно и только одно возможное числовое значение из заранее известной совокупности значений. Случайной величиной дискретного типа (дискретной случайной величиной) называется величина, которая может принимать либо конечное число возможных значений, либо такое бесконечное число значений, которые могут быть расположены в числовую последовательность Е1, Е2, ... . Для каждого из этих значений указывают его вероятность. Сумма этих вероятностей должна быть равна 1. Если случайная величина принимает только одно значение, то соответствующая ему вероятность равна 1.
Пример 1. Пусть Х1 - число “орлов”, выпавших при двух бросках симметричной монеты. Х может принимать значения 0, 1 или 2 с вероятностями, вычисленными по формуле Бернулли: Дискретные случайные величины записывают в виде таблицы. Для данного примера получим:
Верхняя строчка - возможные значения Х1, Р - их вероятности, сумма которых равна 1. С помощью таблицы можно считать вероятности попадания случайной величины дискретного типа в интервалы. Например, для заданной выше случайной величины Х
Пример 2. В полном наборе игры в домино 28 костей. Пусть Х2 – сумма очков на случайно выбранной кости. Поскольку наименьшее значение такой суммы равно 0 («пусто-пусто»), следующее – 1 и так до 12 («6-6»), Х является случайной величиной дискретного типа. Зададим ее таблицей.
Вероятности в этой таблице вычислены по формуле классической вероятности, в числителях дробей количества костей домино с данным числом очков, знаменатели равны общему числу костей. Случайные величины традиционно обозначаются заглавными буквами X, Y, Z, ... , а их возможные значения - прописными: x1, x2, y1, и т. д.
ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
Если F(x) = P(X < x), то функция F(x) называется функцией распределения (интегральной функцией распределения) случайной величины Х, т.е. функция распределения в точке “х” - это вероятность того, что случайная величина Х примет значение, меньшее заданного числа х. Из определения сразу следуют несколько свойств F(x): F(- ¥) = 0, F(+ ¥ ) = 1; F(x) - неубывающая функция (т.е. если x1 < x2 , то F(x1) £ F(x2) ). Функция распределения для случайной величины дискретного типа имеет “ступенчатый” график. Для случайной величины Х1 из §13 F(x) запишется так:
Обратите внимание, что левые концы «ступенек» - выколотые, а правые - нет. Например, F(1) = P(X1 < 1) = P(X1 =0) = 0,25; F(1,1) = P(X1<1,1) = P(X1 = 0) + P(X1 = 1) = 0,75. «Высоты» «ступенек» равны очередным вероятностям, взятым из таблицы : сначала 0,25, затем еще +0,5, и наконец еще +0,25. Аналогичный график и для другого примера – про домино – только там будет не 2, а 12 «ступенек». Справедлива формула: P(a £ X < b) = F(b) - F(a).
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ ДИСКРЕТНОГО ТИПА
Математическое ожидание - важнейшая “характеристика положения” случайной величины. Для дискретной величины она вычисляется по формуле М(Х) = x1 · p1 + x2 · p2 + ... + xk · pk (+...) = где x1, x2, ... , xk, ... - возможные значения случайной величины (верхняя строка таблицы), p1, p2, ..., pk, ... - их вероятности (нижняя строка). Математическое ожидание - это число, которое выражает среднее значение случайной величины (иначе, среднее значение по распределению). Для примера из §13 М(Х1) = 0 · 0,25 + 1 · 0,5 + 2 · 0,25 = 1 . Здесь Х1 - число “орлов”, выпавших при 2 бросках симметричной монеты. М(Х1) - среднее число “орлов”, выпадающих при 2 бросках симметричной монеты, это число равно 1. Для другого примера из §13 М(Х2) = 6. Отметим два простейших свойства математического ожидания: 1. М (С) = С 2. М (С · Х) = С · М(Х) ( С - постоянная ). В дальнейшем нам придется вычислять математическое ожидание случайной величины Х2. Если случайная величина Х задается таблицей
то случайная величина Х2 получится после возведения в квадрат возможных значений случайной величины Х, при этом Р(Х = хк)= = Р(Х2 = хк2) = pk :
Поэтому М(Х2) = x12 · p1 + x22 · p2 + ... + xk2 · pk = В частности, для примера из §13
и М(Х2) = 02 · 0,25 + 12 · 0,5 + 22 · 0,25 = 1,5
|
|
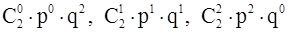 . Т. к. p = q = 0,5 , то эти вероятности равны 0,25; 0,5; 0,25 соответственно.
. Т. к. p = q = 0,5 , то эти вероятности равны 0,25; 0,5; 0,25 соответственно.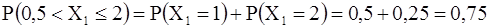 .
.



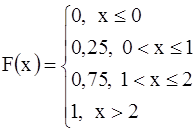
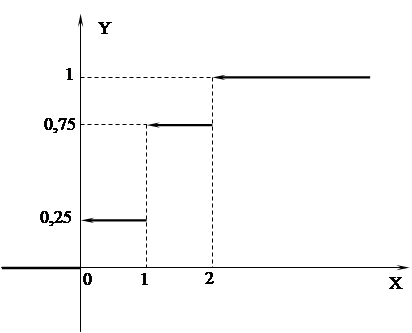
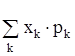 ,
,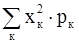 .
.