Обратная связь
|
Автокорреляция в остатках. Критерий Дарбина-Уотсона Автокорреляция в остатках может быть вызвана несколькими причинами, имеющими различную природу.
1. Она может быть связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака.
2. В ряде случаев автокорреляция может быть следствием неправильной спецификации модели. Модель может не включать фактор, который оказывает существенное воздействие на результат и влияние которого отражается в остатках, вследствие чего последние могут оказаться автокоррелированными. Очень часто этим фактором является фактор времени  . .
От истинной автокорреляции остатков следует отличать ситуации, когда причина автокорреляции заключается в неправильной спецификации функциональной формы модели. В этом случае следует изменить форму модели, а не использовать специальные методы расчета параметров уравнения регрессии при наличии автокорреляции в остатках.
Один из более распространенных методов определения автокорреляции в остатках – это расчет критерия Дарбина-Уотсона:
 . (4.5) . (4.5)
Т.е. величина  есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии. есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.
Можно показать, что при больших значениях 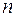 существует следующее соотношение между критерием Дарбина-Уотсона существует следующее соотношение между критерием Дарбина-Уотсона  и коэффициентом автокорреляции остатков первого порядка и коэффициентом автокорреляции остатков первого порядка  : :
 . (4.6) . (4.6)
Таким образом, если в остатках существует полная положительная автокорреляция и 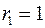 , то , то  . Если в остатках полная отрицательная автокорреляция, то . Если в остатках полная отрицательная автокорреляция, то  и, следовательно, и, следовательно,  . Если автокорреляция остатков отсутствует, то . Если автокорреляция остатков отсутствует, то  и и  . Т.е. . Т.е.  . .
Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза  об отсутствии автокорреляции остатков. Альтернативные гипотезы об отсутствии автокорреляции остатков. Альтернативные гипотезы  и и 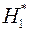 состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам (см. приложение E) определяются критические значения критерия Дарбина-Уотсона состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам (см. приложение E) определяются критические значения критерия Дарбина-Уотсона  и и  для заданного числа наблюдений для заданного числа наблюдений 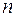 , числа независимых переменных модели , числа независимых переменных модели 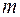 и уровня значимости и уровня значимости 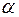 . По этим значениям числовой промежуток . По этим значениям числовой промежуток  разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью  осуществляется следующим образом: осуществляется следующим образом:
 – есть положительная автокорреляция остатков, – есть положительная автокорреляция остатков,  отклоняется, с вероятностью отклоняется, с вероятностью  принимается принимается  ; ;
 – зона неопределенности; – зона неопределенности;
 – нет оснований отклонять – нет оснований отклонять  , т.е. автокорреляция остатков отсутствует; , т.е. автокорреляция остатков отсутствует;
 – зона неопределенности; – зона неопределенности;
 – есть отрицательная автокорреляция остатков, – есть отрицательная автокорреляция остатков,  отклоняется, с вероятностью отклоняется, с вероятностью  принимается принимается 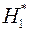 . .
Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу  . .
Пример. Проверим гипотезу о наличии автокорреляции в остатках для аддитивной модели нашего временного ряда. Исходные данные и промежуточные расчеты заносим в таблицу:
Таблица 4.11

| 
| 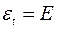
| 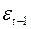
| 
| 
| |
|
|
|
|
|
| |
|
| -5,252
| –
| –
| 27,584
| |
|
| -35,843
| -5,252
| 935,8093
| 1284,7
| |
|
| -74,183
| -35,843
| 1469,956
| 5503,1
| |
|
| 48,937
| -74,183
| 15158,53
| 2394,8
| |
|
| -26,946
| 48,937
| 5758,23
| 726,09
| |
|
| 60,464
| -26,946
| 7640,508
| 3655,9
| |
|
| 45,124
| 60,464
| 235,3156
| 2036,2
| |
|
| 50,244
| 45,124
| 26,2144
| 2524,5
| |
|
| 2,361
| 50,244
| 2292,782
| 5,574
| |
|
| -59,229
| 2,361
| 3793,328
| 3508,1
| |
|
| 41,431
| -59,229
| 10132,44
| 1716,5
| |
|
| -68,450
| 41,431
| 12073,83
| 4685,4
| |
|
| 69,668
| -68,45
| 19076,58
| 4853,6
| |
|
| 36,078
| 69,668
| 1128,288
| 1301,6
| |
|
| -34,263
| 36,078
| 4947,856
|
| |
|
| -50,143
| -34,263
| 252,1744
| 2514,3
| | Сумма
| -0,002
| 50,141
| 84921,85
| 37911,97
| Фактическое значение критерия Дарбина-Уотсона для данной модели составляет:
 . .
Сформулируем гипотезы:  – в остатках нет автокорреляции; – в остатках нет автокорреляции;  – в остатках есть положительная автокорреляция; – в остатках есть положительная автокорреляция; 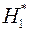 – в остатках есть отрицательная автокорреляция. Зададим уровень значимости – в остатках есть отрицательная автокорреляция. Зададим уровень значимости  . По таблице значений критерия Дарбина-Уотсона определим для числа наблюдений . По таблице значений критерия Дарбина-Уотсона определим для числа наблюдений  и числа независимых параметров модели и числа независимых параметров модели  (мы рассматриваем только зависимость от времени (мы рассматриваем только зависимость от времени  ) критические значения ) критические значения 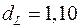 и и  . Фактическое значение . Фактическое значение  -критерия Дарбина-Уотсона попадает в интервал -критерия Дарбина-Уотсона попадает в интервал  (1,37<2,24<2,63). Следовательно, нет основания отклонять гипотезу (1,37<2,24<2,63). Следовательно, нет основания отклонять гипотезу  об отсутствии автокорреляции в остатках. об отсутствии автокорреляции в остатках.
Существует несколько ограничений на применение критерия Дарбина-Уотсона.
1. Он неприменим к моделям, включающим в качестве независимых переменных лаговые значения результативного признака.
2. Методика расчета и использования критерия Дарбина-Уотсона направлена только на выявление автокорреляции остатков первого порядка.
3. Критерий Дарбина-Уотсона дает достоверные результаты только для больших выборок.
Приложение A[6]
Случайные переменные
|
|
 .
. . (4.5)
. (4.5) есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.
есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.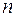 существует следующее соотношение между критерием Дарбина-Уотсона
существует следующее соотношение между критерием Дарбина-Уотсона  :
: . (4.6)
. (4.6)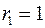 , то
, то  . Если в остатках полная отрицательная автокорреляция, то
. Если в остатках полная отрицательная автокорреляция, то  и, следовательно,
и, следовательно,  . Если автокорреляция остатков отсутствует, то
. Если автокорреляция остатков отсутствует, то  и
и  . Т.е.
. Т.е.  .
. об отсутствии автокорреляции остатков. Альтернативные гипотезы
об отсутствии автокорреляции остатков. Альтернативные гипотезы  и
и 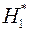 состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам (см. приложение E) определяются критические значения критерия Дарбина-Уотсона
состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам (см. приложение E) определяются критические значения критерия Дарбина-Уотсона  и
и  для заданного числа наблюдений
для заданного числа наблюдений 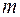 и уровня значимости
и уровня значимости 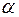 . По этим значениям числовой промежуток
. По этим значениям числовой промежуток  разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью
разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью  осуществляется следующим образом:
осуществляется следующим образом: – есть положительная автокорреляция остатков,
– есть положительная автокорреляция остатков,  принимается
принимается  – зона неопределенности;
– зона неопределенности; – нет оснований отклонять
– нет оснований отклонять  – зона неопределенности;
– зона неопределенности; – есть отрицательная автокорреляция остатков,
– есть отрицательная автокорреляция остатков, 
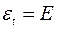
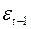


 .
. . По таблице значений критерия Дарбина-Уотсона определим для числа наблюдений
. По таблице значений критерия Дарбина-Уотсона определим для числа наблюдений  и числа независимых параметров модели
и числа независимых параметров модели  (мы рассматриваем только зависимость от времени
(мы рассматриваем только зависимость от времени 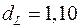 и
и  . Фактическое значение
. Фактическое значение