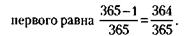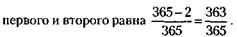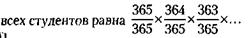|
|
Относительная частота появления в тексте букв русского алфавита
Из таблицы следует, что на каждую тысячу букв в среднем приходится 75 букв а, 17 букв б, 46 букв в и т. д. Получив шифрованное письмо, вам придется лишь подсчитать частоты появления в нем различных секретных значков и сопоставить их с теми частотами, что в таблице. Так, если на тысячу восемьсот букв письма окажется 135 «треугольников», то это означает, что данный значок
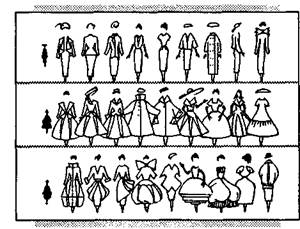
А вот еще один эксперимент – специально для любителей «счастливых» билетов. (Как известно, «счастливым» считается такой трамвайный, автобусный, троллейбусный билет, у которого сумма первых трех цифр равна сумме трех последних). В теории вероятностей существует формула, в соответствии с которой на каждые 100 билетов в среднем 5–6 должны оказаться «счастливыми». И если не полениться собрать необходимую пачку в сто билетов, то можно легко в этом убедиться. «Обязательность» случая была давно подмечена предприимчивыми людьми. В чем смысл игры для хозяина рулетки? Главный «секрет производства» здесь в том, что выпадение цифры 0 – ее называют «зеро» – всегда в пользу хозяина, независимо от того, на «красное» или «черное» поставил игрок свои деньги. За счет этой единственной цифры и существует хозяин рулетки. И не только он. Целое государство Монако живет за счет доходов знаменитого игорного дома в Монте-Карло, где идет крупная игра в рулетку. Трудно придумать более яркий пример использования закономерностей случайных явлений: выход «зеро» определенное число раз столь же обязателен, как, скажем, падение подброшенного камня на землю, хотя каждая отдельная цифра появляется случайно и никакими силами заранее угадана быть не может. И все же Смок Беллью, герой повести Джека Лондона, если вы помните, научился почти безошибочно предугадывать, где остановится шарик. Как ему это удавалось делать? Джек Лондон раскрывает секрет своего любимого героя. Наблюдая за игрой, Смок подметил, что колесо останавливалось не как попало – этого, казалось бы, следовало ожидать, – а по определенным правилам. «Случайно я дважды отметил, где остановился шарик, когда вначале против него был номер девять. Оба раза выиграл двадцать шестой». Столь странное поведение колеса объяснялось тем, что рулетка стояла недалеко от печки: ее деревянное колесо рассохлось и покоробилось. Смоку удалось уловить скрытую от других закономерность поведения колеса. Стоит ли, однако, утверждать, что можно выявить систему у любых – всех проявлений случая? Попробуйте, например, установить общие закономерности изменения моды, формы одежды, которая, безусловно, относится к случайным явлениям. На рис. 8.1 показаны колебания мод женской одежды почти за 50 лет XX века. Срок вполне достаточный, чтобы найти хоть какие-нибудь основательные регулярности. Однако их нет. Все – и форма шляпок, и силуэт платья – меняются «как попало». Остается незыблемым лишь общий принцип: «новое – это прочно забытое старое». Предпринимавшиеся попытки связать капризы моды с мировыми катаклизмами – войнами, экономическими кризисами, даже с солнечной активностью – ни к чему не привели.
Рис. 8.1.Динамика дамской моды
Возможность установления определенного порядка, закономерностей в случайных явлениях, как правило, связана с наличием в них так называемой «устойчивой частоты»: появление интересующего нас события, например рождение младенца мужского пола, при многократном повторении происходит в одинаковой доле от общего числа рождений. Поисками закономерностей в случайных явлениях занимается специальная, хорошо разработанная в наши дни наука – статистика. Именно статистика после многих наблюдений над случаем делает заключение о том, устойчива ли частота его появления. Когда такую устойчивость удается обнаружить, статистики говорят о наличии статистического ансамбля. Изучением закономерностей в случайных явлениях занимается теория вероятностей. Познакомимся с основами этой науки. Как и многие другие понятия, слово «вероятность» с его производным «вероятно» входит в нашу жизнь с детства. Мы говорим: вероятно, вечером будет дождь; я, вероятно, простудился и т. п. « Вероятно» в этих привычных фразах означает «возможно» – этим словом субъективно оценивается возможность наступления интересующего нас случайного события в будущем. Если же появляется необходимость показать степень этой возможности, мы уточняем: «весьма вероятно», «маловероятно», «совершенно невероятно». Более четкие градации, чем «много» и «мало», в обиходном языке не предусмотрены. Между тем жизненные задачи требуют оценки вероятности более конкретной, чем «много» или «мало». Сегодня на морском транспорте сказать: вероятно, будет (или не будет) происшествие – это значит не сказать почти ничего. Степень возможности появления будущего случайного события – вероятность – должна быть оценена объективно точно, определенным числом. Самый старый, так называемый классический способ измерения вероятности – по частоте наступления интересующего нас события. Это можно сделать весьма просто: прийти в тир, выстрелить все 100 раз и сосчитать число попаданий в мишень. Доля, которую это число составит от общего числа выстрелов, и есть частота попаданий. Скажем, попали 70 раз – частота равна 0,7, или семидесяти процентам. Вот эта самая частота и принимается за вероятность. Но что значит «принимается»? Почему не сказать просто: вероятность – это и есть частота интересующего нас события? По той же самой причине, по которой мы различаем вчерашнюю сводку погоды и прогноз на завтра. Частота -это результат события, которое уже произошло, вероятность – предсказание того, что должно случиться в будущем. Сказать: «Вероятность попадания 70 процентов» – значит предположить, что при очередной стрельбе 70 пуль из ста попадут в мишень. Это предположение мы делаем в уверенности, что соотношение шансов попасть – не попасть, которое определилось во время уже состоявшейся стрельбы, сохранится и на будущее. При этом, разумеется, предполагается, что условия стрельбы: оружие, расстояние до мишени, размеры мишени и т. д. – останутся неизменными. Применительно к бизнесу это означает, что если при определенных условиях в прошлом мы получали, на каждые 100 рублей 30 рублей прибыли, то при повторении ситуации в будущем сохранится и прибыль. Откуда, однако, у нас берется уверенность, что «дальше будет, как раньше»? К этому нас подводит весь многовековой коллективный опыт человечества. Когда народ говорит, например, «У семи нянек дитя без глаза», «Тише едешь – дальше будешь» или утверждается, что «бутерброд падает маслом вниз», – это не только о прошлом, но и о будущем. Если в течение многих лет люди наблюдают, как из 100 куриных яиц появляется примерно поровну петушков и курочек, то нет основания не верить, что и на следующий год шансы появления петушка останутся прежними. В слове «вероятно» явственно прослушивается «надеюсь». Это дало основание магистру философии Вильнюсского университета Сигизмунду Ревковскому – первому, кто в 1829– 1830 годах стал преподавать в России (тогдашней) теорию вероятностей, – определить вероятность как «меру надежды». Итак, для того чтобы рассчитать вероятность во многих распространенных жизненных задачах, достаточно произвести весьма элементарное арифметическое вычисление – разделить число случаев, благоприятствующих интересующему нас событию, на общее число всех возможных случаев.
Важно отметить, что чем больше опытов проведено при определении частоты, тем точнее, объективнее получается вероятность. Это проявление одного из важнейших законов, управляющих случаем, – так называемого закона больших чисел. Классический способ определения вероятностей и его формула и сегодня находят широкое применение. Если нам, скажем, известно, что среди тридцати экзаменационных билетов три очень трудных, то можно быстро прикинуть вероятность вытащить трудный билет, как Представьте себе, что вы получили перед какой-либо жеребьевкой весьма обнадеживающую информацию: организатор кладет плохие билеты не как попало, а снизу, видно стараясь, чтобы они оказались подальше от испытуемых. Это, конечно, хорошо: стоит теперь вытянуть билет сверху – и вероятность заполучить выгодный номер резко увеличится. Но вот какой она станет? Узнать это с помощью классической формулы невозможно. Формула применима лишь тогда, когда все рассматриваемые случаи равновозможны – любой билет должен иметь одинаковые шансы попасть в руки испытуемого. Стоит исключить эту равновозможность, и классическая формула перестает работать. Следовательно, правильно эту формулу записать так:
Откуда же мы знаем, равновозможны случаи или нет? На этот вопрос отвечает опыт.Причем опыт, который не обязательно ставить. Бывает, вполне достаточно провести его мысленно. Допустим, вы собрались сыграть с товарищем в шахматы. Кому играть белыми, должен решить жребий. Ваш партнер в одной руке зажимает белую фигуру, в другой – черную. Какова вероятность, что вы будете играть белыми? Каждый из нас, не задумываясь, назовет 50 процентов. Но почему? Это результат мысленного опыта: мы инстинктивно оцениваем шансы отгадать любую фигурку как равновероятные, и поскольку белых фигур ровно половина, то это и будет интересующая нас вероятность. Вот еще один пример. Многим читателям, видимо, доводилось слышать о такой дикой игре армейского захолустья царской России. В барабан многозарядного револьвера закладывается лишь один патрон, после чего барабан несколько раз проворачивается. Затем участники игры по очереди приставляют револьвер к виску и нажимают на спуск. Так вот, для того чтобы сказать, чему равна при этом вероятность проигрыша, явно нет необходимости ставить эксперимент. Так же как и при отгадывании шахматной фигуры, равновозможность шансов здесь очевидна из соображения о симметрии возможных исходов. И вероятность проигрыша – получения пули – для того, кто стреляет первым, в расчете на 5 патронов равна:
Вполне можно ограничиться мысленным экспериментом и там, где равновозможность шансов очевидна из геометрического представления задачи. Скажем, в офисе проложен телефонный кабель длиной 60 метров, из которых 3 метра приходится на труднодоступное место. Спрашивается, какова вероятность в случае выхода кабеля из строя, что повреждение случится именно на труднодоступном участке?
Такую вероятность иногда называют геометрической – ведь она получена путем сопоставления длин двух отрезков. И соображение о равновозможности шансов (уверенность в том, что появление неисправности возможно в любом месте кабеля) в этом случае исходит из наглядных, геометрических представлений. Интуитивное определение вероятности, выработанное человеком и ходе многовековой эволюции, не раз выручало его в сложных ситуациях. Принимая решение «что лучше», «что быстрее», «какова мера опасности», люди, сами того не ведая, часто основывают свой выбор на интуитивной вероятной оценке. «Лучше поездом, чем самолетом», «Поеду-ка я трамваем, автобуса не дождаться», «Сегодня стоит надеть плащ» – во всех этих решениях явно просматривается учет возможности случая. С интуитивным определением вероятности тесно связан так называемый принцип практической уверенности. Принцип этот можно сформулировать так: «Если вероятность события мала, то следует считать, что в однократном опыте – в данном конкретном случае – это событие не произойдет. И наоборот – при большой вероятности событие следует ожидать». В повседневной жизни мы широко, сами то не подозревая, пользуемся этим важным принципом. Скажем, собираясь лететь в отпуск самолетом, мы уверены в том, что нас доставят на места в целости и сохранности: не пишем завещание, даем телеграмму с просьбой встретить т. п. Тем самым мы интуитивно принимаем, что вероятность аварии самолета равна нулю – событие невозможное, хотя эта вероятность всегда имеет некоторое, правда весьма небольшое, но все же отличное от нуля значение. Вероятность же нашей доставки до места соответственно но принимается равной единице – событие это считается достоверным. Оценивая практическую невозможность или достоверность события и принимая на этой основе решение, мы, однако, далеко не всегда связываем свой выбор с предельными, крайним значениями вероятности. Величина вероятности, которая нас практически устраивает, зависит от того, какова важность последствий принятого нами решения. Решение надеть плащ может быть принято и в том случае, если вероятность дождя, скажем, 70–80 %. Но вряд ли мы решимся прыгнуть с парашютом, узнав, что у него такая же (70–80 %) надежность. Итак, вероятность– это степень возможности появления будущего случайного события Руководствуясь этим определением, решим несколько примеров. Примеры расчетов на будущее ПРИМЕР 1 «Я пришла к тебе против своей воли,– сказала она твердым голосом,– но мне велено исполнить твою просьбу. Тройка, семерка и туз выиграют тебе сряду...» Вероятность события, предсказанного пушкинской «пиковой дамой», легко подсчитать с помощью классической формулы. Общее число равновозможных шансов при этом будет равно количеству всех вариантов, в которых могут быть взяты три любые карты из колоды. Считая, что в колоде Германна было 52 карты, это число равно количеству сочетаний из 52 по 3. Заглянув в учебник или справочник по математике, с помощью формул комбинаторики – раздела математики, изучающего комбинации перестановки предметов, получаем 44 200 сочетаний. Числом благоприятствующих шансов здесь будет количество возможных вариантов, включающих заветные карты из той же колоды. Например, сначала какую-нибудь одну из четырех троек, затем одну из четырех семерок, наконец, один из четырех тузов. Годится и любой другой порядок – он значения для Германна не имеет. Общее число таких благоприятствующих сочетаний равно 12. Применив классическую формулу, получим:
Пушкин совершенно правильно оценил ситуацию: при такой ничтожной вероятности Германн мог рассчитывать только на чудо... С помощью классической формулы легко подсчитать, например, вероятность такого обычно небезразличного нам события, как выигрыш в лотерею. Вот типичный пример условий денежно-вещевой лотереи. На каждый разряд, включающий 10 000 лотерейных билетов, приходится 120 денежных и 80 вещевых выигрышей. Какова вероятность выиграть деньги, вещь или хоть что-нибудь по одному лотерейному билету? Решение столь простой задачи под силу ученику начальной школы, стоит лишь применить классическую формулу:
В последнем расчете мы суммируем в числителе дроби, так как число благоприятствующих шансов складывается из количества денежных и вещевых выигрышем. Несколько сложнее дело обстоит с числовой лотереей, примером которой может служить некогда популярное у нас спортлото. Здесь не все отдано на откуп случаю: каждый участник может избирать номера для вычеркивания по своему полному усмотрению. Участники спортлото как бы играют друг с другом. Однако, как мы сейчас убедимся, и здесь места для случая остается вполне достаточно. Какова, например, в числовой лотерее вероятность вычеркнуть правильно все 6 номеров из 49? Подсчитано, что вычеркивание 6 цифр из 49 может быть произведено почти 14 миллионами различных способов (точная цифра 13 983 816). Следовательно, вероятность единственного правильного вычеркивания равна
Отгадать 5 цифр – это значит указать ошибочно одну из нужных шести. Такую ошибку можно сделать 258 способами. Значит, именно таковы шансы, благоприятствующие угадыванию 5 номеров. А вероятность этого события по классической формуле равна
Четыре номера угадает, естественно, значительно больше людей, число благоприятствующих шансов повышается здесь до 13 545. И вероятность, соответственно, будет выше:
И наконец, вероятность угадать три номера равна
Все это ничтожно мало. Но зато в утешение любителей подобных лотерей теория вероятностей может несколько поднять их шансы на выигрыш (не зря ведь вероятность – мера надежды). Вычеркивая цифры, мы обычно не следим за тем, какую долю составляют среди вычеркнутых однозначные. И порой таких оказывается половина, а то и больше. Так делать не следует. Ведь из 49 цифр карточки однозначных всего 9. И следовательно, вероятность выпадания на них выигравшего номера составляет всего
Эту цифру легко проверить, взяв подряд 100 номеров, выигравших в спортлото. Из них около 18 будут однозначными. Значит, вычеркивать цифры тоже нужно с учетом этой вероятности: если у вас одна карточка, из шести вычеркнутых цифр лишь одна должна быть однозначной; если десять карточек, то на девяти вычеркивать по одной однозначной цифре, а на десятой – две. На непосредственном подсчете основано и свойственное всем людям интуитивное определение вероятности. Скажем, нас спрашивают, что вероятнее, отгадать в спортлото правильно 3 или 4 номера? Мы, не задумываясь, без всякого расчета отвечаем – три. (Правда, мы вряд ли сможем сообразить без расчетов, что для трех номеров вероятность выше почти в 20 раз!) Вот еще несколько примеров, когда интуиция оказывается несостоятельной. ПРИМЕР 2 Теория вероятностей утверждает, что случайные события, те, которые мы стремимся предсказать, иногда могут происходить довольно часто. Можно произвести такой опыт. Если в вашей учебной группе юношей и девушек примерно поровну, попытайтесь предугадать, кто сейчас первым войдет в помещение: он или она? Сказав «он», вы рискуете ошибиться лишь в половине всех случаев – около 50 % ваших предсказаний обязательно оправдаются. Зато если вы рискнете предсказать, что оба вошедших подряд окажутся юношами, вероятность резко упадет и окажется равной всего 25 % (по теореме умножения 0,5 х 0,5). Ваше предсказание сбудется лишь в одном случае из четырех. Существует, однако, нехитрый способ добиться значительного увеличения числа «вещих» предсказаний. Для этого нужно только загадать, кто войдет, несколько по-иному: если вы будете утверждать, что юношей окажется не меньше, чем один из нескольких вошедших подряд, то это ваше предсказание имеет значительно больше шансов на успех. Расчет, сделанный по правилам теории вероятностей, показывает, что вероятность увидеть хотя бы одного юношу из пяти вошедших равна 93 %. Делая такое предсказание, вы практически ничем не рискуете – оно сбудется наверняка. С высокой точностью сбудется также и предсказание прихода не менее двух юношей (или, если хотите, девушек – это в подобных задачах не имеет значения) из пяти вошедших. Вероятность этого события равна 81 %. Тоже высокая вероятность. И даже предсказывая, что из пяти человек не менее трех окажутся лицами названного вами пола, вы все еще сохраняете шансы прослыть пророком – вероятность 50 %. Приведем для разных случаев маленькую, но полезную табличку, взятую из теории вероятностей (табл. 8.5).
Таблица 8.5
Вероятности прихода предсказанного количества мужчин или женщин (в %)
Посмотрев табличку, вы можете уверенно предсказать, например, что из пяти вошедших будет не менее двух мужчин (или женщин). Вероятность этого события очень большая – 81 %. В восьми случаях из десяти ваше предсказание сбудется. Этот пример поможет нам приоткрыть один из профессиональных секретов гадалок и прочих прорицателей. Предположим, гадалка предсказывает пять каких-то событий, которые могут равно как произойти, так и не произойти – точно так же, как в одинаковой степени могут войти мужчина и женщина. Такими предсказаниями могут быть, например, «приятная встреча», «лихой недруг», «дальняя дорога», «получение известия», «нечаянная радость» и т. п. Вероятность того, что сбудутся все пять предсказаний, как показывает расчет, исключительно мала – всего 3,1 %. Но легковерному человеку вполне достаточно, если состоится хотя бы не менее двух-трех из них. Заметьте, не менее – это может быть и два, и три, и четыре, и даже пять. А такое количество пророчеств – мы уже знаем – происходит с высокой вероятностью – 81 %. Поэтому-то часть сделанных гадалкой предсказаний обычно и сбывается. А легковерные люди и не подозревают, что приобщились к «таинствам» теории вероятностей. Помимо математической стороны дела есть и не менее важные причины психологического происхождения. Вот некоторые из них. Прорицатели, как правило, люди наблюдательные. Вороша карты или перемешивая кофейную гущу, они нет-нет да и ненароком бросят взгляд на доверчивого клиента. Не болезненный ли у него вид («лихой недуг»), не горит ли его взор лихорадочным ожиданием («нечаянная радость»)? Богатый профессиональный опыт подсказывает гадалке, что, кому и как говорить. Не последнюю роль играет и чутье, интуиция. Предсказатели издавна эксплуатируют и то, что человеку свойственно принимать желаемое за действительное. Оракул так формулирует свое откровение, что понимать его можно самым различным образом – как хочется «заказчику». Вспомним предсказание, сделанное дельфийским оракулом Крезу: «Если ты нападешь на персов, великое государство погибнет». Очень уж хотелось Крезу разрушить чужое государство. Вот он и поверил. А государство-то погибло его собственное. Из множества сделанных предсказаний люди запоминают обычно лишь те, что сбылись. Несбывшиеся пророчества в памяти людей, как правило, не сохраняются. Но стоит сбыться нескольким предсказаниям из множества сделанных, как это немедленно поднимается суеверными людьми на щит, обрастает фантастическими подробностями, обретает достоверность «факта». ПРИМЕР 3 Какова вероятность совпадения дней рождения у любых двух человек, например, из вашей группы в 30 студентов? На первый взгляд кажется, что поскольку в году 365 дней, то возможность такого совпадения весьма невелика, что-нибудь около Вначале определим вероятность празднования дня рождения какого-нибудь студента в один из дней года. Здесь число всех возможных случаев – это число возможных дней рождения в году – 365. Число интересующих нас случаев – дней рождения одного человека в году – тоже 365. Вероятность празднования дня рождения студентом в один из дней года равна Действительно, можно с полной уверенностью сказать, что любой человек за год отпразднует свой день рождения. Теперь возьмем любого второго студента и найдем вероятность того, что его день рождения не совпадает с днем рождения первого студента. Число всех возможных случаев – возможных дней рождения в году – остается здесь, конечно, тем же – 365, а вот число интересующих нас случаев уменьшится на 1 – ведь тот день, когда праздники могут совпадать, надо выбросить. Итак, вероятность несовпадения дня рождения второго студента с днем рождения
Затем возьмем любого третьего студента вашей группы и найдем подобным же образом, что вероятность несовпадения с днем рождения
И далее для всех студентов группы – в том же духе. Зададим себе такой вопрос: а какова вероятность того, что и у первого, и у второго, и у третьего, и у всех остальных студентов дни рождения не совпадут? Вероятности таких событий находят с помощью умножения. Вероятность несовпадения дней рождения у
Число сомножителей равно общему числу студентов. В нашем случае таких сомножителей должно быть 30. Стоит перемножить, и получится, что вероятность несовпадения дней рождения у всех тридцати студентов равна 0,29. А то, что нас интересует,– вероятность совпадения – мы найдем путем вычитания этой цифры из единицы. Вероятность совпадения дней рождения у любых двух студентов из тридцати равна 1 - 0,29 = 0,71. Это высокая вероятность. Значит, почти наверняка в любом коллективе, где 30 человек, есть люди, родившиеся в один день. А как быть тем коллективам, где число людей 10, 40 или 50, т. е. отличается от 30? На этот случай пригодится готовая таблица вероятностей совпадения дней рождения для разных групп людей – от 5 до 100 и более человек (табл. 8.6). Как она рассчитывается, мы уже знаем. Таблица 8.6
|
|
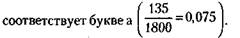
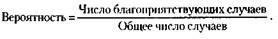
 = 0,1, или 10 процентов. И если бы можно было таким простым способом рассчитывать вероятности во всех случаях, то учебники по теории вероятностей (а заодно и данная глава) были бы много тоньше. К большому сожалению, столь просто рассчитывать вероятность удается далеко не всегда.
= 0,1, или 10 процентов. И если бы можно было таким простым способом рассчитывать вероятности во всех случаях, то учебники по теории вероятностей (а заодно и данная глава) были бы много тоньше. К большому сожалению, столь просто рассчитывать вероятность удается далеко не всегда.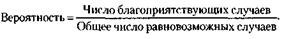
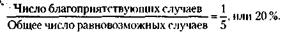
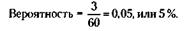
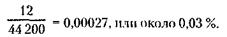

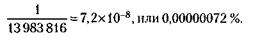
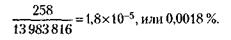
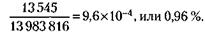
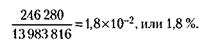
 , или 18,4%.
, или 18,4%. = 0,08, или 8 %. Это грубая ошибка. На самом деле следует рассуждать так.
= 0,08, или 8 %. Это грубая ошибка. На самом деле следует рассуждать так.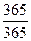 = 1.
= 1.