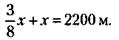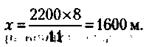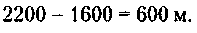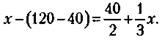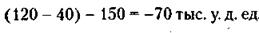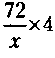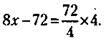|
|
Относительные уровни издержек на предприятиях 5 главаПереходя к целым числам (для этого нужно умножить дробные доли на их общий знаменатель, равный 12), получим долю А равной 15, долю Б-10 и долю В- 18. 1) Исходя из долей, определим суммы, причитающиеся каждому компаньону: компаньону А причитается
компаньону Б – 20 х 10 = 200 тыс. у. д. ед., компаньону В – 20 х 18 = 360 тыс. у, д. ед. 2) Из условия задачи и полученных долей ясно, что старший компаньон (В) владеет предприятием 6 лет (что в три раза меньше 18). Значит, в соответствии с долями компаньон А владеет предприятием 9. Обозначим через х сумму кредита, тогда по условиям задачи суммы выплат и остатки будут следующими:
Помятуя, что выплаты заканчиваются в месяце, следующем за тем, в котором остаток на единицу больше, чем номер месяца, прошедшего с момента получения кредита определим, чему может быть равна сумма кредита, исходящая из этого условия. Для остатка 1-го месяца
Для остатка 2-го месяца
Для остатка 3-го месяца
Для остатка 4-го месяца
x1, х2, х4 (и т. д.) не подходят, потому что по условию задачи сумма кредита должна находиться в пределах 50 - 100 млн у. д. ед. Следовательно: 1) Условию задачи отвечает сумма кредита, равная х3 = 66 млн у. д. ед. 2) Кредит должен быть погашен к концу 4-го месяца. 3) Плата за кредит равна 3 % х 4 месяца, т. е. 12 % от 66 млн у. д. ед., что соответствует 7,92 млн у. д. ед.
10. 1) Обещание было дано в понедельник. 2) Деньги будут отданы в ближайшую пятницу. 11.Обозначим через х капитал игрока, у – сумму ставки на победу, z – сумму ставки на поражение. Тогда условие задачи можно записать так:
Решая совместно (1) и (2), получим:
Далее, из (1) и (2):
Подставляя полученные значения у и z в (3), будем иметь:
Итак: 1) капитал игрока был равен 200 тыс. у. д. ед.; 2) сумма ставки на победу равна 30 тыс. у. д. ед.; 3) сумма ставки на поражение равна 20 тыс. у. д. ед.
12. Обозначив расстояние от Санкт-Петербурга до бензоколонки через а, а от бензоколонки до Верхнениженска через б, сообразим в соответствии с условием задачи, что расстояние от поселка Закат до бензоколонки – Следовательно, от поселка Закат до поселка Рассвет Искомая плата за проезд, таким образом, равна: 100 : 10= 10 у. д. ед.
13. Это возможно. Разместив участок III так, как показано на рисунке, нетрудно убедиться, что: III = I – а – в + а + а + б = I + а – в + б. С другой стороны, II = а - в + б. Следовательно, III = I + II.
Кстати, мы только что доказали теорему Пифагора. Стороны квадратов I и II – это катеты, а стороны квадрата III – гипотенуза АБВ: сумма квадратов катетов равна квадрату гипотенузы. Просто и наглядно.
14. 1) Обозначая площадь, занимаемую оборудованием из контейнера № 1, через x, условие задачи можно математически записать так: – площадь, занимаемая оборудованием из контейнера № 2, равна x + 10; – площадь, занимаемая оборудованием из контейнера № 3, равна х + 20. х+ (х+ 10) + (x + 20) = 402;
3x + 30 = 402; x =124м2. Соответственно, площади, занимаемые оборудованием из контейнеров № 2 и № 3, равны 134м2 и 144м2. 2) Обозначим черз п, т и k число раз, во сколько площади цехов А, Б и В больше, чем площади оборудования из контейнеров № 1, № 2 и № 3. По условию задачи n,m и k могут иметь значения лишь 1, 1,5 и 2 каждое. При этом должно иметь место равенство:
124 х n + 134 х m +144 х k = 613. (*)
Будем рассуждать так: – если п = 1,5 или 2, то при любых возможных значениях т и k сумма (*) будет меньше 613; следовательно, п может быть равно только 1, а значит, контейнер № 1 предназначен для цеха Б и для значения т остается только 1,5 или 2; – при этом если т = 2, то при любых возможных п и k сумма (*) будет меньше 613; следовательно, т может быть равно только 1,5, а значит, контейнер № 2 оказывается предназначен для цеха В; – для k, таким образом, остается только 2, и контейнер № 3 оказывается предназначенным для цеха А. 15.Обозначая вес контейнера с товаром через х, а вес контейнера через у, можно математически записать условие задачи так: х + (х + 2) = 8, откуда х = 3 тонны. 3 = y + 0,5y, откуда у = 2 тонны.
Следовательно, вес товара равен: 3 - 2 = 1 тонна. 16. Да, это так. Парное число получается путем деления первого числа (а) на (а - 1). Так, если первый партнер внес 3 млн, то второй должен внести
При этом сложение капитала даст 17. Необходимо первую бочку ставить строго по центру площадки, а все остальные ставить симметрично от центра по отношению к каждой очередной бочке другого предприятия. 18. Рассмотрим два численных примера. 1) Если ребро малого ящика равно 1 м, то длина, которую занимает груз, равна 1 + 2 x 1 = 3 погонных метра, и стоимость перевозки, исходя из длины груза, составляет 20 х 3 = 60 у. д. ед. При этом объем груза равен 13 +(2 x 1)3 =9м3, и стоимость перевозки, исходя из объема, составляет 20 х 9 = 180 у. д. ед. Следовательно, оплата с погонного метра значительно (в три раза) выгоднее. 2) Если ребро малого ящика равно 0,5 м, то длина, которую занимает груз, равна 0,5 + 2 х 0,5 =1,5 погонных метра, и стоимость перевозки, исходя из длины груза, составляет 20 х 1,5 = 30 у. д. ед. При этом объем груза равен (0,5)3 +(2 x 0,5)3 =1,125м3, и стоимость перевозки, исходя из объема, составляет 20 х 1,125 = = 22,50 у. д. ед. Следовательно, оплата здесь существенно выгоднее с объема (на 25 % дешевле). Таким образом, ответ на вопрос задачи – какого вида оплата выгоднее – неоднозначен и зависит от размера груза. Интересно и полезно узнать граничное значение этого размера – то, при котором оба вида оплаты равноценны. Обозначим через х длину ребра малого ящика, при которой наступит равенство погонного и объемного размеров, учитываемых при оплате. При этом будет иметь место следующее очевидное равенство: х + 2х х = х3 + (2 х х) , или 3x =9x3.
Итак, если ребро малого ящика короче 0,5 м, выгоднее платить исходя из объема, а если длиннее – исходя из длины. Проверим это утверждение. При длине ребра малого ящика 0,58 м длина груза составит 0,58 + 2 х 0,58 = 1,74 погонных метра и стоимость перевозки будет равна 20 х 1,74 = 35 у. д. ед. При этом объем груза будет (0,58)3 +(2 x 0,58)3 = 1,74м3 и стоимость перевозки остается без изменений. 19. Первый шаг: поменять местами контейнеры 2 и 1. Второй шаг: поставить 5-й и 6-й после 7-го. Третий шаг: поставить 1-й и 3-й после 4-го. Четвертый шаг: 6-й и 8-й перенести в начало.
20. Обозначим количество приборов до прохождения ими контроля через х; количество приборов, оставшихся после прохождения 1-й ступени контроля, через х1, второй ступени контроля – х2 и т. д. При этом условие задачи можно математически записать следующим образом:
21.1) Прежде всего найдем высоту прилегающего к шару цилиндра, равного шару по объему. Объем шара равен Объем прилегающего цилиндра, имеющего высоту, равную диаметру шара (так называемый описанный цилиндр), равен Отношение объема шара и цилиндра будет:
Следовательно, для того чтобы прилегающий к шару цилиндр имел объем, равный объему 2 шара, высота цилиндра должна составлять 2) Теперь задача сводится к нахождению суммарной длины того количества отрезков нити длиной по 0,4 м, которое укладывается в цилиндр с диаметром основания 0,6 м (как в пачке вермишели). Площадь основания цилиндра равна:
Площадь сечения нити –
Длина нити равна суммарной длине этих отрезков, т. е. 9 х 106 х 0,4 м = 3 600 000 м, или 3600 км. 3) Количество катушек, необходимое, чтобы смотать эту нить, равно:
22.1) Обозначим через х количество дней, за которое подразделение П1 смогло бы самостоятельно израсходовать весь складской запас, если бы он состоял только из цемента марки Б. При этом условие задачи можно записать так:
Откуда 140 + х = 5х; х = Поскольку фактически количество цемента Б на складе равно половине возможного запаса, подразделение П1 израсходует имеющийся цемент Б за половину срока:
2) Обозначим через у количество дней, за которое подразделение П2 смогло бы самостоятельно израсходовать весь складской запас, если бы он состоял только из цемента марки А. При этом:
Откуда 210 + 2у = 7у; у = 42 дня. А фактически – половина этого запаса – за 21 день. Но поскольку подразделения берут цемент совместно, то подразделение П2 к моменту, когда подразделение П1 выберет весь свой цемент Б, не успеет получить полностью свой цемент А. И то, что останется, они будут брать в дальнейшем сообща. Сколько же на это потребуется времени? 3) За те 17 17 Но так как фактически запас цемента А равен половине складского, то после истечения 17 Известно, что оба подразделения способны израсходовать весь складской запас цемента марки А за 30 дней, следовательно, А всего оба подразделения выберут весь цемент за 17
23. Обозначая через х и у возраст первого и последнего филиала соответственно, запишем условие задачи следующим образом:
Решая систему из двух уравнений с двумя неизвестными, получим: х = 5у; 5у - у = 8,
откуда х = 2, у = 10.
24. Скорость судна при движении в реке по течению равна против течения - 1) Скорость судна при движении в море (без течения) равна средней скорости движения по течению и против него (то, что течение в одном случае добавляет, в другом отнимает):
25. Обозначим общее число работников через х, тогда условие задачи можно записать так:
количество электриков равно количество механиков Откуда:
8 х 2(х - 1) + 3 х 3 (х - 1) = 8 х 3 х х; х = 25.
Количество электриков равно:
Количество механиков равно:
(включая головного сборщика).
26. Из второго условия задачи следует, что панели А и Б весят одинаково, а также что Следовательно, панели А и Б весят по 200 х 3 = 600 кг.
27. Обозначим через х стоимость обыкновенной акции. Тогда условие задачи можно записать так:
Решая уравнение, получим:
Всего по условию задачи 250 х 4 = 100 акций. Из них обыкновенных 1000 - 250 = 750. Следовательно, на 1 обыкновенную акцию предполагается выплатить
Количество привилегированных акций 250, следовательно, на 1 привилегированную акцию предполагается выплатить 28. Обозначим через х общее количество стиральных машин четырех модификаций, собранных всеми двенадцатью предприятиями, и равные ему количества электронных и механических элементов, необходимых для их создания. Тогда количество электронных элементов четырех модификаций, необходимых для сборки машин на одном предприятии, будет равно
Интересующее нас минимальное количество этих элементов (xmin) будет иметь место при равенстве:
А на всех трех электронных предприятиях должно производиться 144 х 3 = 432 элемента каждой модификации, что дает возможность собрать 432 стиральные машины всех четырех модификаций. При этом на каждом предприятии будет производиться по 432 : 12 = 36 стиральных машин всех четырех модификаций. Проследим последовательность действий при кооперации предприятий от начала до конца: – каждое из трех электронных предприятий производит 432 : 3 = 144 электронных элемента четырех модификаций (36 х 4); – каждое из девяти механических предприятий производит 432: 9 = 48 механических элементов; – затем каждое электронное предприятие передает каждому механическому предприятию по 12 электронных элементов четырех модификаций (3 х 4), оставляя у себя 36 электронных элементов; – а каждое механическое предприятие передает каждому электронному предприятию по 4 механических элемента, оставляя у себя 36 таких элементов; – в результате на каждом из двенадцати электронных и механических предприятий оказывается по 36 электронных и по 36 механических элементов, из которых производится по 36 стиральных машин четырех модификаций. Общее же количество стиральных машин равно 36 x 12 = 432. 29.Обозначим через хn общее количество производственных помещений, предназначенных для распределения очередной n-й паре, а через Нn и Чn – количество помещений, выделенных предприятиям этой пары соответственно нечетных и четных номеров. Тогда по условиям задачи будут иметь место следующие очевидные соотношения:
По условиям задачи для последней пары
(так как каждой очередной паре достается равное количество ресурсов, а Н следующей пары на единицу больше, Ч должно быть на единицу меньше). Следовательно, из (2) следует:
По условиям задачи это равенство должно иметь место для любой пары, поэтому с учетом
а также
Поскольку для последней пары, где Чn = 0, Нn = 6 - 0 = 6, а для первой пары Н1 может быть минимально равно 0, при этом Ч1 = 6 - 0 = 6. По условиям задачи от пары к паре количество производственных помещений для нечетных предприятий увеличивается на единицу, в распределении может участвовать всего 7 пар (имеющих Нn от 0 до 6, включая 0), т. е. 7 х 2 = = 14 малых предприятий. При этом в соответствии с (*):
Итак: 1) Ресурсы могут распределяться между 14 малыми предприятиями. 2) Всего распределяется 42 производственных помещения. Торговых точек для уравнивания возможностей МП должно быть столько, чтобы у каждого предприятия было по 6 единиц ресурсов, т. е. каждая пара предприятий должна получить по 6 торговых точек, а всего 6 x 7 пар предприятий = 42 торговые точки. 3) Количество ресурсов обоих видов, полученных каждым предприятием, будет следующим:
30. Оказывается, это довольно просто. Дело в том, что, к счастью аудитора, суммы цифр в обоих слагаемых оказались кратны 9, а значит – слагаемые делятся на 9. Естественно, делились на 9 они и до перестановки в них цифр. При сложении же чисел, делящихся на 9, сумма также делится на 9. Это означает, что сумма цифр результата сложения должна быть кратна 9. Сложив цифры суммы (кроме подделанной), получим 30. Ближайшее большее число, кратное 9, это 36. Нам не хватает 36 - 30 = 6. Следовательно, исправленная цифра – это 6. 31. Обозначим через х площадь арендуемого фирмой помещения, а через у – количество единиц продукции, идущих в уплату аренды. Тогда условие задачи можно записать так:
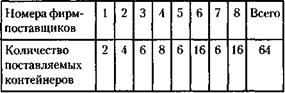
32. Обозначим через т, п, р, q количество контейнеров, поставляемых фирмами первой четверки (не обязательно в порядке последовательности фирм), которые являются партнерами соответствующих (в порядке номеров) фирм второй четверки (т - поставка партнера фирмы № 5, п - фирмы № 6 и т. д.). При этом условие задачи можно записать так:
(44 –это разность общего количества контейнеров и 20 – числа контейнеров, поставляемых первой четверкой: 2 + 4 + 6 + 8 = 20).
Умножая обе части (2) на 2, получим:
Из последнего выражения следует, что q может быть равно только 4, ибо по условиям задачи: 1) q, m,p должны быть целыми положительными числами, 2) эти числа различны и могут быть только 2, 4, 6, 8, 3) 2 не подходит, так как при этом т = р, 4) 6 и 8 не подходят, так как при этом т - р>8. Итак, q = 4. Тогда из (*) следует, что 2(4-2) = m-р, т- р = 4. Последняя разность может иметь место лишь при следующих значениях пары т и р:
Первая пара не подходит, так как число 4 уже имеет «хозяина» – ему равно q. Следовательно, т = 6р = 2. Для п остается лишь значение, равное 8.
Если выстроить значение этих показателей по ранжиру (р, q, т, п), то эта последовательность и будет соответствовать последовательности номеров фирм-партнеров из второй четверки фирмам первой четверки (где была последовательность т, п, р, q): фирма № 5 является партнером фирмы № 3, фирма № 6 является партнером фирмы № 4, фирма № 7 является партнером фирмы № 1, фирма № 8 является партнером фирмы № 2. Подставляя соответствующие значения в (1), нетрудно рассчитать количество контейнеров, поставляемых фирмами второй четверки. Итоговые данные по поставкам всеми фирмами будут следующими:
33.Обозначим начальные фонды, равные у обоих предприятий, через х. Тогда к моменту окончания первой операции предприятие А обладало фондом в размере, равном х + 30, а предприятие Б – х - 30 тыс. у. д. ед. К моменту окончания второй операции фонд предприятия А составлял:
34. Взнос предпринимателя В, равный 320 тыс. у. д. ед., составляет Теперь нужно разделить сумму, равную взносу В, между А и Б так, чтобы у каждого из них оказалось по 35. Обозначим через длину отрезка проволоки, причитающейся владельцу Б. Тогда условие задачи можно будет записать так:
Решая это уравнение, получим:
Владельцу А будет причитаться:
36. Обозначим через х стоимость месячного содержания помещений. Тогда условие задачи можно записать так:
Откуда, после преобразований, х = 150 тыс. у. д. ед. Вычитая полученную стоимость содержания помещений из дохода, получим величину ежемесячных потерь арендатора:
37. Обозначим через х количество участков для субаренды. Тогда выручка за субаренду составит 8х, годовой заработок будет равен
и условие задачи запишется так:
|
|
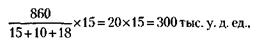
 = 5 лет, а компаньон Б –
= 5 лет, а компаньон Б –  = 3 года и 4 месяца.
= 3 года и 4 месяца.







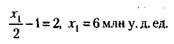
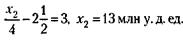
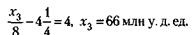
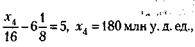
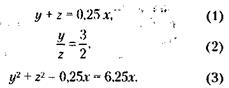
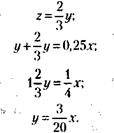
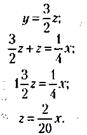
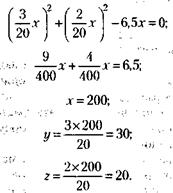
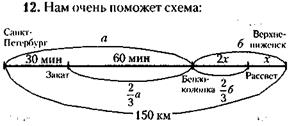
 а, а от бензоколонки до поселка Рассвет
а, а от бензоколонки до поселка Рассвет  т. е. две трети пути от Санкт-Петербурга до Верхнениженска, что составляет
т. е. две трети пути от Санкт-Петербурга до Верхнениженска, что составляет 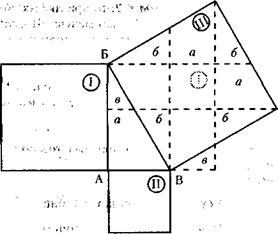

 млн, как и его умножение:
млн, как и его умножение: 
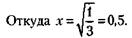

 где R – радиус шара.
где R – радиус шара. R3.
R3.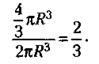
 м.
м.
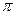 (0,1 мм)2. Количество отрезков нити, укладывающихся в наш цилиндр, равно:
(0,1 мм)2. Количество отрезков нити, укладывающихся в наш цилиндр, равно: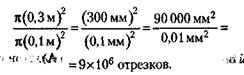
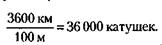

 = 35 дней.
= 35 дней.
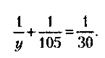
 дня, что подразделение П1 выберет весь цемент Б, подразделение П2 успеет выбрать
дня, что подразделение П1 выберет весь цемент Б, подразделение П2 успеет выбрать всего складского запаса (если бы он состоял только из цемента А).
всего складского запаса (если бы он состоял только из цемента А). всего складского запаса цемента А.
всего складского запаса цемента А. этого запаса за 30 :
этого запаса за 30 : 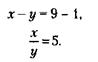
 км/мин (20 км/ч). Скорость
км/мин (20 км/ч). Скорость км/мин (12 км/ч).
км/мин (12 км/ч).
 ,
, .
.
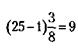
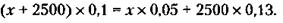
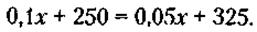

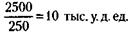
 , а количество элементов одной модификации
, а количество элементов одной модификации 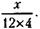 При этом количество этих элементов, производимых на каждом из трех электронных предприятий, должно быть равно,
При этом количество этих элементов, производимых на каждом из трех электронных предприятий, должно быть равно,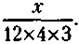
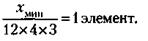
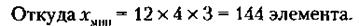

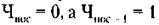
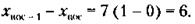
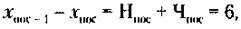
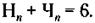



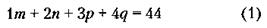
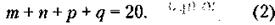


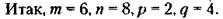

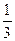 прежнего складского капитала. Значит, весь этот капитал был равен 320 х 3 = 960 тыс. у. д. ед. Причем в этом капитале доли А и Б относились как 1,5 : 1, т. е. были соответственно равны 576 и 384 тыс. у. д. ед.
прежнего складского капитала. Значит, весь этот капитал был равен 320 х 3 = 960 тыс. у. д. ед. Причем в этом капитале доли А и Б относились как 1,5 : 1, т. е. были соответственно равны 576 и 384 тыс. у. д. ед.